Соотношения Крамерса — Кронига | это... Что такое Соотношения Крамерса — Кронига? (original) (raw)

Соотноше́ния Кра́мерса — Кро́нига — интегральная связь между действительной и мнимой частями любой комплексной функции, аналитичной в верхней полуплоскости. Часто используются в физике для описания связи действительной и мнимой частей функции отклика физической системы, поскольку аналитичность функции отклика подразумевает, что система удовлетворяет принципу причинности, и наоборот [1]. В частности, соотношения Крамерса — Кронига выражают связь между действительной и мнимой частями диэлектрической проницаемости.

Определение

Для комплексной функции χ(ω) = χ1(ω) + _i_χ2(ω) комплексной переменной ω, аналитичной в верхней полуплоскости ω и стремящейся к нулю при $|\omega| \rightarrow \infty,$ соотношения Крамерса — Кронига записываются следующим образом:

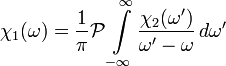
$\chi_1(\omega) = {1 \over \pi} \mathcal{P} \int \limits_{-\infty}^{\infty} {\chi_2(\omega') \over \omega' - \omega}\,d\omega'$

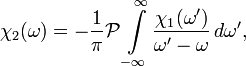
$\chi_2(\omega) = -{1 \over \pi} \mathcal{P} \int \limits_{-\infty}^{\infty} {\chi_1(\omega') \over \omega' - \omega}\,d\omega',$

где символ 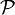$\mathcal{P}$ означает взятие интеграла в смысле главного значения (по Коши). Видно, что χ1(ω) и χ2(ω) не являются независимыми, а значит, полная функция может быть восстановлена, если задана только её действительная или мнимая часть.

В более компактной форме:

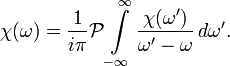
$\chi(\omega) = {1 \over i \pi} \mathcal{P} \int \limits_{-\infty}^\infty {\chi(\omega') \over \omega'-\omega}\,d\omega'.$

Соотношения Крамерса — Кронига в физике

Важным примером применения соотношений Крамерса — Кронига в физике является выражение дисперсионных соотношений в классической электродинамике. В этом случае 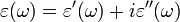$\varepsilon(\omega) = \varepsilon^\prime(\omega) + i\varepsilon^{\prime\prime}(\omega)$ — диэлектрическая проницаемость, ω — частота.

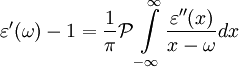
$\varepsilon^\prime(\omega) -1 = \frac{1}{\pi} \mathcal{P} \int\limits_{-\infty}^\infty \frac{\varepsilon^{\prime\prime}(x)}{x-\omega} dx$

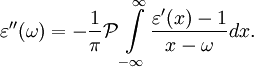
$\varepsilon^{\prime\prime}(\omega) = - \frac{1}{\pi} \mathcal{P} \int\limits_{-\infty}^\infty \frac{\varepsilon^\prime(x) -1}{x-\omega} dx.$

Действительная и мнимая части диэлектрической проницаемости определяют соответственно показатели преломления и поглощения данной среды; таким образом, эти показатели не являются независимыми друг от друга.

История

Соотношения Крамерса — Кронига названы в честь Ральфа Кронига [2] и Хендрика Крамерса[3].

Примечания

↑ John S. Toll, Causality and the Dispersion Relation: Logical Foundations, Physical Review, vol. 104, pp. 1760—1770 (1956).
↑ R. de L. Kronig, On the theory of the dispersion of X-rays, J. Opt. Soc. Am., vol. 12, pp. 547—557 (1926).
↑ H.A. Kramers, La diffusion de la lumiere par les atomes, Atti Cong. Intern. Fisica, (Transactions of Volta Centenary Congress) Como, vol. 2, p. 545—557 (1927) .