Вес топологического пространства | это... Что такое Вес топологического пространства? (original) (raw)

Вес топологического пространства

База топологии (базис топологии, открытая база, база топологического пространства X) — семейство 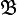$\mathfrak{B}$ открытых подмножеств X такое, что каждое открытое множество 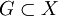$G\subset X$ является объединением элементов 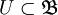$U\subset \mathfrak{B}$ . Понятие базы — одно из основных в топологии. Во многих вопросах, относящихся к открытым множествам некоторого пространства, достаточно ограничиться рассмотрением элементов его базы. Пространство может иметь много баз, наибольшую из которых образует семейство всех открытых множеств.

Часто базу топологии предъявляют для того, чтобы ввести топологию на множестве X, когда она ещё не была задана. Для этого достаточно, чтобы система множеств 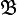$\mathfrak{B}$ , претендующая быть базой новой топологии, покрывала пространство X и была бы замкнутой относительно операции пересечения (это свойство иногда добавляют к определению базы топологии). Если такая система множеств задана, тогда открытыми множествами пространства X принимаются все подмножества в X, представимые объединением произвольного семейства множеств — элементов базы.

Примеры

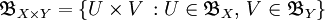
$\mathfrak{B}_{X\times Y} = \{U\times V\,: U\in\mathfrak{B}_X,\,V\in\mathfrak{B}_Y\}$
При этом топология на 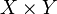$X\times Y$ не будет зависеть от того, какие базы пространств X и Y используются для её задания. Такая топология называется (стандартной) топологией декартова произведения топологических пространств.

Связанные определения

Минимум мощностей всех баз называется весом топологического пространства X.
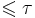- В пространстве веса τ существует всюду плотное множество мощности $\leqslant \tau$ .
- Пространства со счетной базой называются также пространствами со второй аксиомой счетности.
Локальной базой пространства X в точке (базой точки x) называется семейство 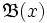его открытых множеств, обладающее свойством: для любой окрестности O x точки x найдется элемент 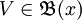такой, что .
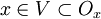- Пространства, имеющие счетную локальную базу в каждой точке, называются пространствами с первой аксиомой счетности.
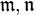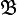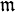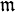Пусть $\mathfrak{m},\mathfrak{n}$ — некоторые кординальные числа. База $\mathfrak{B}$ пространства X называется $\mathfrak{m}$ -точечной, если каждая точка $x \in X$ принадлежит не более чем $\mathfrak{m}$ элементам семейства 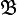$\mathfrak{B}$ . В частности, при 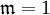$\mathfrak{m}=1$ база называется дизъюнктной, при конечном 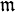$\mathfrak{m}$ — точечно конечной, при 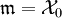$\mathfrak{m}=\mathcal{X}_0$ — точечно счетной.
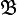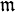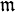База $\mathfrak{B}$ пространства X называется $\mathfrak{m}$ -локальной, если для каждой точки $x \in X$ существует ее окрестность O x, пересекающаяся с не более чем $\mathfrak{m}$ элементами семейства 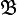$\mathfrak{B}$ . В частности, при 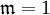$\mathfrak{m}=1$ база называется дискретной, при конечном 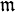$\mathfrak{m}$ — локально конечной, при 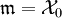$\mathfrak{m}=\mathcal{X}_0$ — локально счетной.
База 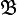называется 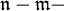-точечной (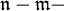-локальной), если она является объединением множества мощности 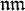-точечных (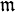-локальных) баз. Таковы, например, при 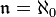σ-дизъюнктные, σ-точечно конечные, σ-дискретные, σ-локально конечные базы.
- Эти понятия находят применение главным образом в критериях метризуемости пространств. Так, пространство со счетной базой или с первой аксиомой счетности и точечно счетной базой метризуемо; регулярное пространство с σ-дискретной или с σ-локально конечной базой метризуемо (обратное верно только для первого утверждения).
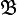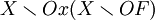База $\mathfrak{B}$ пространства X называется равномерной (_k_-равномерной), если для каждой точки $x \in X$ (каждого бикомпактного подмножества F) и каждой ее (его) окрестности O x(O F) лишь конечное число элементов базы содержит x (пересекается с F) и одновременно пересекается с дополнением $X\smallsetminus Ox(X\smallsetminus OF)$ . Пространство X метризуемо тогда и только тогда, когда оно является паракомпактом с равномерной базой (колмогоровским, или _T_0-пространством с _k_-равномерной базой).
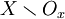База $\mathfrak{B}$ пространства X называется регулярной, если для каждой точки $x \in X$ и произвольной её окрестности O x существует такая окрестность O'x, что множество всех элементов базы, пересекающихся одновременно с O'x и $X\smallsetminus O_x$ , конечно.

Свойства

Объекты, определённые в терминах баз

Упорядоченная топология обычно определяется как топология порождённая набором открыто-интервальных множеств.
Метрическая топология обычно определяется как топология порождённая набором открытых шаров.
Вторично-счётное пространство — это то, которое имеет счётную базу.
Дискретная топология имеет в качестве базы синглетон.

Вариации и обобщения

Литература

Александров П. С., Колмогоров А. Н. Введение в общую теорию множеств и функций, М.—Л., 1948
Урысон П. С., Труды по топологии и другим областям математики, т. 1—2, М.—Л., 1951
Пасынков Б. А., Введение в теорию размерности. Введение в втеорию топологических пространств и общую теорию размерности, М., 1973
Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974
Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Вес топологического пространства" в других словарях:

Вес (значения) — Вес: В физике: Вес сила воздействия тела на опору или подвес. Удельный вес отношение веса вещества к его объёму. Статистический вес, в квантовой механике и квантовой статистике число различных квантовых состояний с данной… … Википедия
ВЕС — топологического пространства наименьшее кардинальное число, являющееся мощностью открытой базы, топологич. пространства. В., наряду с мощностью, важнейший инвариант топологич. пространства. п. С. Александров … Математическая энциклопедия
МОЩНОСТНАЯ ХАРАКТЕРИСТИКА — топологического пространства функция, сопоставляющая этому пространству бесконечное кардинальное число и принимающая одинаковые значения на гомеоморфных пространствах. М. х. наз. также кардинальными инвариантами. Областью определения М. х. может… … Математическая энциклопедия
СЕТЬ — топологического простран с т в а X семейство подмножеств этого пространства такое, что для каждой точки и каждой ее окрестности Ох найдется элемент М семейства такой, что Семейство всех одноточечных подмножеств пространства и каждая его база… … Математическая энциклопедия
РАЗМЕРНОСТЬ — топологического пространства X целочисленный инвариант dim X, определяемый следующим образом. Тогда и только тогда dim X = 1, когда . О непустом тополо гич. пространстве Xговорят, что оно не более чем n мерно, и пишут dim , если в любое конечное… … Математическая энциклопедия
БИКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в каждом открытом покрытии к рого содержится конечное подпокрытие того же пространства. Следующие утверждения равносильны: 1) пространство Xбикомпактно; 2) пересечение любой центрированной системы замкнутых в… … Математическая энциклопедия
АБСОЛЮТ — 1) А. регулярного топологического пространства X пространство аХ, обладающее тем свойством, что оно совершенно и неприводимо отображается на X, а всякий совершенный неприводимый прообраз пространства аХ гомеомор фен пространству аХ. У каждого… … Математическая энциклопедия
ОБЩАЯ ТОПОЛОГИЯ — ветвь геометрии, посвященная исследованию непрерывности и предельного перехода на том естественном уровне общности, к рый определяется природой этих понятий. Исходными понятиями О. т. являются понятия топологического пространства и непрерывного… … Математическая энциклопедия