Всюду плотное множество | это... Что такое Всюду плотное множество? (original) (raw)
Всюду плотное множество
Всюду плотное множество
Пло́тное мно́жество — подмножество, точками которого можно приблизить любую точку объемлющего пространства.
Содержание
Определения
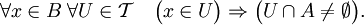
- Множество A называется всюду плотным, если оно плотно в X.
Замечание
Приведённое выше определение плотности множества эквивалентно любому из нижеперечисленных:
Примеры
См. также
Ссылки
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Всюду плотное множество" в других словарях:
- ВСЮДУ ПЛОТНОЕ МНОЖЕСТВО — Атопологического пространства X множество, определяемое свойством: , где замыкание множества А. Другими словами, в любом открытом в Xмножестве имеется хотя бы одна точка из множества А. Употребляется также термин плотное множество . А. А. Мальцев … Математическая энциклопедия
- ПЛОТНОЕ МНОЖЕСТВО — то же, что всюду плотное множество. Более общо, множество Аназ. плотным в открытом множестве Gпространства X, если G содержится в замыкании Аили, что то же самое, если всюду плотно в подпространстве . Если Ане плотно ни в каком непустом открытом… … Математическая энциклопедия
- Плотное множество — подмножество пространства, точками которого можно сколь угодно хорошо приблизить любую точку объемлющего пространства. Формально говоря, A плотно в X, если всякая окрестность любой точки x из X содержит элемент A. Содержание 1 Определения 2… … Википедия
- Нигде не плотное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- Связное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
- ВПОЛНЕ НЕПРИВОДИМОЕ МНОЖЕСТВО — множество Млинейных операторов в локально выпуклом топологическом векторном пространстве Е, всюду плотное в алгебре S(E).всех слабо непрерывных линейных операторов в Е;при этом S(E).рассматривается в слабой операторной топологии. Понятие В. н. м … Математическая энциклопедия