Равномерно темперированный строй | это... Что такое Равномерно темперированный строй? (original) (raw)

Равноме́рно темпери́рованный строй — музыкальный строй, при котором каждая октава делится на математически равные интервалы, чаще всего на двенадцать полутонов (1:\sqrt[12]{2}). Такой строй господствует в европейской профессиональной музыке приблизительно с XVIII века вплоть до нашего времени.

Содержание

История

12-ступенный равномерно темперированный строй возник в обстановке поисков учёными разных специальностей «идеального» строя. Исторически предшествующий натуральный строй имел ряд недостатков — прежде всего, не позволял транспонировать и модулировать в достаточно большое количество тональностей без возникновения существенных диссонансов.

Невозможно с достоверностью указать, кто именно изобрёл равномерную темперацию. Среди первых учёных, предлагавших практические способы деления октавы на 12 равных интервалов,— Генрих Грамматеус (1518) и Винченцо Галилей (1581).

Одним из первых авторов, давших теоретическое обоснование 12-ступенной равномерной темперации, был китайский принц Чжу Цзайюй (朱載堉), в трактате 1584 года[1][2]. В Европе примерно в то же время исследования математической задачи равномерного деления октавы проводил фламандский математик Симон Стевин. Написанный около 1585 года на его родном языке труд «О теории певческого искусства», в котором Стевин дал математически точный расчёт равномерной темперации, был опубликован спустя 300 лет, в 1884 году.

Непосредственным предшественником равномерно темперированного в Европе был «хорошо темперированный» строй — целое семейство неравномерных темпераций, тем не менее позволявших вполне успешно играть в любой из тональностей. Одним из теоретиков и пропагандистов[3] такого строя был Андреас Веркмейстер — немецкий композитор и органист. Многие исследователи разделяют мнение, что «Хорошо темперированный клавир» Иоганна Себастьяна Баха, хорошо знакомого с работами Веркмейстера, написан для инструментов именно с такой неравномерной темперацией[4].

Одними из первых теоретиков нового равномерно темперированного строя были В. Галилей (отец Галилео) и М. Мерсенн. У нового строя было много оппонентов[5]. Равномерно темперированный строй нарушал строгую пропорцию интервалов, как следствие, в аккордах начали появляться небольшие биения. В глазах многих теоретиков это было посягательством на чистоту музыки. Андреас Веркмейстер[6] утверждал, что в новом строе все аккорды (подразумевались прежде всего трезвучия) становились однообразными и симметричными, в то время как в старых строях из-за неравномерности темперации каждый аккорд имел своё неповторимое (акустическое) звучание. Однако со временем равномерная темперация завоевала признание и стала фактическим стандартом.

Вычисление частот звуков

Можно математически вычислить частоты для всего звукоряда, пользуясь формулой:

f(i) = f_0 \cdot 2^{i/12} ,

где f0 — частота камертона (например Ля 440 Hz), а i — количество полутонов в интервале от искомого звука к эталону f0.

Последовательность вычисленных таким образом частот образует геометрическую прогрессию:

например, можно вычислить частоту звука на тон (2 полутона) ниже от камертона Ля — ноты соль:

i=-2

f(-2) = 440\,\mathrm{Hz} \cdot 2^{-2/12} \approx {391,995}\,\mathrm{Hz}

если нам надо вычислить ноту Соль, но на октаву (12 полутонов) выше:

i=12-2=10

f(10) = 440\,\mathrm{Hz} \cdot 2^{10/12} \approx {783,991}\,\mathrm{Hz}

Частоты двух полученных нот Соль отличаются в два раза, что дает чистую октаву. Преимущества равномерной темперации также в том, что можно произвольно транспонировать пьесу на произвольный интервал вверх или вниз.

Сравнение с натуральным строем

Равномерно темперированный строй очень легко можно отобразить в виде измерения интервалов в центах

Тон C1 C# D Eb E F F# G G# A B H C2
Цент 0 100 200 300 400 500 600 700 800 900 1000 1100 1200

Следующая таблица показывает отличия интервалов равномерно-темперированного ряда с натуральным

Интервал Равномерно темперированные интервалы Натуральные интервалы Разница в центах
Прима \sqrt[12]{2^0} = 1 = 0\,\mathrm{Cent} \frac{1}{1} = 1 = 0\,\mathrm{Cent} 0
Малая секунда \sqrt[12]{2^1} = \sqrt[12]{2} \approx 1{,}059463 = 100\,\mathrm{Cent} \frac{16}{15} \approx 1{,}066667 \approx 111{,}73\,\mathrm{Cent} −11,73
Большая секунда \sqrt[12]{2^2} = \sqrt[6]{2} \approx 1{,}122462 = 200\,\mathrm{Cent} \frac{9}{8} = 1{,}125 \approx 203{,}91\,\mathrm{Cent} −3,91
Малая терция \sqrt[12]{2^3} = \sqrt[4]{2} \approx 1{,}189207 = 300\,\mathrm{Cent} \frac{6}{5} = 1{,}2 \approx 315{,}64\,\mathrm{Cent} −15,64
Большая терция \sqrt[12]{2^4} = \sqrt[3]{2} \approx 1{,}259921 = 400\,\mathrm{Cent} \frac{5}{4} = 1{,}25 \approx 386{,}31\,\mathrm{Cent} 13,69
Кварта \sqrt[12]{2^5} = \sqrt[12]{32} \approx 1{,}334840 = 500\,\mathrm{Cent} \frac{4}{3} \approx 1{,}333333 \approx 498{,}04\,\mathrm{Cent} 1,96
Тритон \sqrt[12]{2^6} = \sqrt{2} \approx 1{,}414214 = 600\,\mathrm{Cent} \frac{45}{32} \approx 1{,}406250 \approx 590{,}22\,\mathrm{Cent} 9,78
Квинта \sqrt[12]{2^7} = \sqrt[12]{128} \approx 1{,}498307 = 700\,\mathrm{Cent} \frac{3}{2} = 1{,}5 \approx 701{,}96\,\mathrm{Cent} −1,96
Малая секста \sqrt[12]{2^8} = \sqrt[3]{4} \approx 1{,}587401 = 800\,\mathrm{Cent} \frac{8}{5} = 1{,}6 \approx 813{,}69\,\mathrm{Cent} −13,69
Большая секста \sqrt[12]{2^9} = \sqrt[4]{8} \approx 1{,}681793 = 900\,\mathrm{Cent} \frac{5}{3} \approx 1{,}666667 \approx 884{,}36\,\mathrm{Cent} 15,64
Малая септима \sqrt[12]{2^{10}} = \sqrt[6]{32} \approx 1{,}781797 = 1000\,\mathrm{Cent} \frac{16}{9} \approx 1{,}777778 \approx 996{,}09\,\mathrm{Cent} 3,91
Большая септима \sqrt[12]{2^{11}} = \sqrt[12]{2048} \approx 1{,}887749 = 1100\,\mathrm{Cent} \frac{15}{8} = 1{,}875 \approx 1088{,}27\,\mathrm{Cent} 11,73
Октава \sqrt[12]{2^{12}} = 2 = 1200\,\mathrm{Cent} \frac{16}{8} = 2 = 1200\,\mathrm{Cent} 0

Расчёт конкретных высот применительно к клавиатуре фортепиано

Примечание. Значения частот рассчитаны исходя из стандартной частоты камертона ля1 = 440 Гц.

Субконтроктава

Охватывает звуки с частотами от 16,352 Гц (включительно) до 32,703 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 2 (или два штриха). В научной нотации имеет номер 0-й

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 16,352 До2 C2 C0 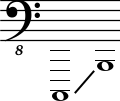Субконтроктава
2 18,354 Ре2 D2 D0
3 20,602 Ми2 E2 E0
4 21,827 Фа2 F2 F0
5 24,500 Соль2 G2 G0
6 27,500 Ля2 A2 A0
7 30,868 Си2 H2 B0

Контроктава

Охватывает звуки с частотами от 32,703 Гц (включительно) до 65,406 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 1 (или один штрих). В научной нотации имеет номер 1.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 32,703 До1 C1 C1 Контроктава
2 36,708 Ре1 D1 D1
3 41,203 Ми1 E1 E1
4 43,654 Фа1 F1 F1
5 48,999 Соль1 G1 G1
6 55,000 Ля1 A1 A1
7 61,735 Си1 H1 B1

Большая октава

Охватывает звуки с частотами от 65,406 Гц (включительно) до 130,81 Гц. Наименования ступеней записываются с большой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 2.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 65,406 До C C2 Велика октава
2 73,416 Ре D D2
3 82,406 Ми E E2
4 87,307 Фа F F2
5 97,999 Соль G G2
6 110,00 Ля A A2
7 123,47 Си H B2

Малая октава

Охватывает звуки с частотами от 130,81 Гц (включительно) до 261,63 Гц. Наименования ступеней записываются с маленькой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 3.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 130,81 до c C3 Мала октава
2 146,83 ре d D3
3 164,81 ми e E3
4 174,61 фа f F3
5 196,00 соль g G3
6 220,00 ля a A3
7 246,94 си h B3

Первая октава

Включает звуки с частотами от 261,63 Гц (включительно) до 523,25 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 1 (или один штрих). В научной нотации имеет номер 4.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 261,63 до1 c1 C4 Перша октава
2 293,67 ре1 d1 D4
3 329,63 ми1 e1 E4
4 349,23 фа1 f1 F4
5 392,00 соль1 g1 G4
6 440,00 ля1 a1 A4
7 493,88 си1 h1 B4

Вторая октава

Включает звуки с частотами от 523,25 Гц (включительно) до 1046,5 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 2 (или два штриха). В научной нотации имеет номер 5.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 523,25 до2 c2 C5 Друга октава
2 587,33 ре2 d2 D5
3 659,26 ми2 e2 E5
4 698,46 фа2 f2 F5
5 783,99 соль2 g2 G5
6 880,00 ля2 a2 A5
7 987,77 си2 h2 B5

Третья октава

Включает звуки с частотами от 1046,5 Гц (включительно) до 2093,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 3 (или три штриха). В научной нотации имеет номер 6.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 1046,5 до3 c3 C6 Третья октава
2 1174,7 ре3 d3 D6
3 1318,5 ми3 e3 E6
4 1396,9 фа3 f3 F6
5 1568,0 соль3 g3 G6
6 1760,0 ля3 a3 A6
7 1975,5 си3 h3 B6

Четвертая октава

Включает звуки с частотами от 2093,0 Гц (включительно) до 4186,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 4 (или четыре штриха). В научной нотации имеет номер 7.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 2093,0 до4 c4 C7 Четвертая октава
2 2349,3 ре4 d4 D7
3 2637,0 ми4 e4 E7
4 2793,8 фа4 f4 F7
5 3136,0 соль4 g4 G7
6 3520,0 ля4 a4 A7
7 3951,1 си4 h4 B7

Пятая октава

Включает звуки с частотами от 4186,0 Гц (включительно) до 8372,0 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 5 (или пять штрихов). В научной нотации имеет номер 8.

Номер ступени Частота, Гц Слоговое обозначения по Гельмгольцу Буквенное обозначение по Гельмгольцу Американская нотация Классическая музыкальная нотация
1 4186,0 до5 c5 C8 Пятая октава
2 4698,6 ре5 d5 D8
3 5274,0 ми5 e5 E8
4 5587,7 фа5 f5 F8
5 6271,9 соль5 g5 G8
6 7040,0 ля5 a5 A8
7 7902,1 си5 h5 B8

Другие равномерные темперации

Существуют и другие равномерные темперации (РТ). Чтобы выражение _n_-тоновая РТ писать короче, может быть использовано сокращение _n_-тРТ[источник не указан 102 дня], где числу n соответствует количество тонов на октаву. Известны музыкальные произведения, написанные в 19-тРТ[7], 24-тРТ, 31-тРТ[8] и даже 53-тРТ[9]. Термин «равномерная темперация», без уточнений, обычно понимается как 12-тРТ.

Равномерные темперации могут также делить иной интервал, не только октаву, на целое число равных ступеней. Чтобы избежать неясности, в англоязычной литературе, например, широко используется словосочетание «equal divisions of an octave», или его сокращённая форма EDO. В русском языке одинаковый смысл передаёт словосочетание «равные деления октавы», или РДО. Поэтому 12-тРТ может переименовываться в 12РДО, 19-тРТ в 19РДО, и так далее[10].

Равномерно темперированный строй и другие строи

Наряду с господствующим равномерно темперированным строем в Европе существовали и существуют другие строи. Русский исследователь музыки XIX века Владимир Одоевский, например, написал так:

Русский простолюдин с музыкальным дарованием, у которого ухо еще не испорчено ни уличными шарманками, ни итальянскою оперою, поет весьма верно; и по собственному чутью берет интервал весьма отчетливо, разумеется, не в нашей уродливой темперированной гамме <...> Я записывал с голоса [известного нашего русского певца Ивана Евстратиевича Молчанова, человека с чудною музыкальною организациею] весьма интересную песню: «У Троицы, у Сергия, было под Москвою» <...> заметил, что Si певца никак не подходит к моему фортепианному Si; и Молчанов также заметил, что здесь что-то не то <...> Это навело меня на мысль устроить фортепиано нетемперированное в такой системе, как обыкновенное. За основание я принял естественную гамму, вычисленную акустическими логарифмами по методе Прони; в этом энгармоническом клавицине все квинты чистые, диезы, отмеченные красным цветом, отделены от бемолей и по невозможности в самом механизме инструмента, я пожертвовал faЬ и utЬ, чтобы сохранить si# и mi#, потому что наши народные певцы — по непонятной для меня причине поют более в диезных нежели в бемольных тонах

— В. Ф. Одоевский[11]

Широкомасштабное движение музыкантов-аутентистов практикует воспроизведение музыки прошлого в тех строях, в которых исполняемая ими музыка была написана.

В неевропейской традиционной музыке сохраняется практика использования строев, отличающихся от равномерно темперированного, — во всех жанрах и формах мощной макамо-мугамной традиции[12], а также в индийской[13] и др.

См. также

Примечания

  1. ↑ Hart R. Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China
  2. ↑ См. en:Zhu Zaiyu, Prince of Zheng
  3. ↑ См. Werckmeister A. Musicae mathematicae hodegus curiosus… (1687), Musikalische Temperatur, oder… (1691)
  4. ↑ Bach J. S. J. S. Bach: The Well-Tempered Clavier. — Los Angeles, CA: Alfred Music Publishing, 2004. — P. 4. — ISBN 0882848313
  5. ↑ Например, Тартини и др.
  6. ↑ Веркмейстер в своей работе Musikalische Paradoxal-Discourse (1707), опубликованной посмертно, выступил популяризатором идей Мерсенна о равномерно темперированном строе.
  7. ↑ Nine Preludes for Two Pianos in 19-Tone Temperament by Joel Mandelbaum
  8. ↑ Concert No. 2 for two violins and orchestra by Henk Badings, 1969
  9. ↑ Letter from B. Cicovacki to P. Scaruffi (англ.):

    ... Иосип Славенски написал произведение для электронных инструментов с названием «Музыка в Натуральной тональной системе» (1937). В нём две части, первая написана для фисгармонии Бозанкета с 53 тонами в октаве...»

    («_…JOSIP STOLCER SLAVENSKI <...> composed a composition for electronic insruments with the title Music in the Natural Tonal System (1937). It includes two movements: the first movement is written for the Bosanquet enharmonium with 53 tones in an octave_»)

  10. ↑ Алиева И. Микротональная нотация посредством числовых уточнений знаков альтерации (на примере звукоряда тара)
  11. ↑ Одоевский В. Ф. [«Русскии простолюдин...»]. Цит. из сборника В. Ф. Одоевский. Музыкально-литературное наследие.— М.: Государственное музыкальное издательство, 1956.— с. 481—482
  12. ↑ В отечественной науке на это указывал, начиная с конца 1920-х годов, выдающийся музыковед и этнограф В. М. Беляев; см. например, его работы: Туркменская музыка. Том 1. М., 1928 (совм. с В. А. Успенским); Руководство для обмера народных музыкальных инструментов, М., 1931; Музыкальные инструменты Узбекистана, М., 1933; Ладовые системы в музыке народов СССР // В.М.Беляев. [Сб. статей]. М.: Сов. композитор, 1990. Среди современных публикаций — доклад С. Агаевой и Ш. Гаджиева «О проблемах исследования звуковысотной системы азербайджанских мугамов». VII Междунар. симпозиум науч.-иссл. группы «Макам» при Междунар. Совете по трад. муз. ЮНЕСКО. Баку. 2011. С. 20-32; см. также упомянутую статью И. Алиевой. Краткий обзор и библиографию зарубежной литературы по данной тематике см. в O. Wright et al. Arab Music. I. Art Music // The New Grove Dictionary of Music and Musicians. London, New York, 2001; H. Farhat. Iran. II. Classical traditions. 2. Theory of intervals and scales, 3. The modal system. // ibid. Также см. 'Issam El-Mallah. Arab Music and Musical Notation. Hans Schneider Verlag. Tutzing. 2001; S. Marcus. The Interface between Theory and Practice: Intonation in Arab Music. Asian Music, Vol. 24, No. 2 (1993), pp. 39-58; H. Farhat. Scales and Intervals: Theory and Practice, Irish Musical Studies, i (1990), pp. 216–26.
  13. ↑ Краткий обзор и библиографию зарубежной литературы по данной тематике см. в Powers H. and Widdess R. India, subcontinent of. III. Theory and practice of classical music. 1. Tonal systems // The New Grove Dictionary of Music and Musicians. London, New York, 2001.
Музыкальный строй
Пифагорейский строй • Натуральный строй • Среднетоновый строй • Равномерно темперированный строй