Инверсия (перестановка) | это... Что такое Инверсия (перестановка)? (original) (raw)

Инверсия (перестановка)

Инверсия (перестановка)

Перестано́вка — это упорядоченный набор чисел 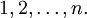1, 2,\dots, n. При этом n называется порядком перестановки. Число всех перестановок порядка n равно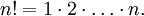 n!=1\cdot 2\cdot\dots\cdot n.

Более общо, перестановкой произвольного (хотя обычно конечного) множества X называется биекция 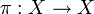\pi: X\to X .

Содержание

Свойства

Связанные определения

Специальные типы перестановок

Подстановки и произведения циклов

Перестановка π множества X может быть записана в виде подстановки, например:

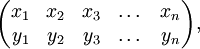
\begin{pmatrix} x_1 & x_2 & x_3 & \dots & x_n \\ y_1 & y_2 & y_3 & \dots & y_n\end{pmatrix},

где 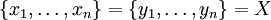\{x_1,\dots, x_n\}=\{y_1,\dots, y_n\}=X и π(x i) = y i.

Перестановку также можно записать в виде произведения непересекающихся циклов, причем единственным образом с точностью до порядка следования циклов в произведении. Например:

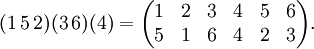
(1\, 5\, 2)(3\, 6)(4)=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 5 & 1 & 6 & 4 & 2 & 3\end{pmatrix}.

Случайная перестановка

Случайной перестановкой называется называется случайный вектор ξ = (ξ1,...,ξ_n_), все элементы которого принимают натуральные значения от 1 до n, и при этом вероятность совпадения любых двух элементов равна 0.

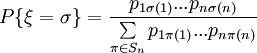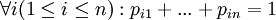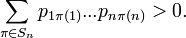Независимой случайной перестановкой называется такая случайная перестановка ξ, для которой P\{\xi=\sigma\}=\frac{p_{1\sigma(1)}...p_{n\sigma(n)}}{\sum\limits_{\pi \in S_n}p_{1\pi(1)}...p_{n\pi(n)}} для некоторых p i j, для которых \forall i (1\le i \le n): p_{i1}+...+p_{in}=1 и \sum\limits_{\pi \in S_n}p_{1\pi(1)}...p_{n\pi(n)}>0. Если при этом p i j не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть 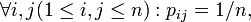\forall i,j (1\le i,j \le n): p_{ij}=1/n, то ξ называют однородной.

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Инверсия (перестановка)" в других словарях: