Инъективность | это... Что такое Инъективность? (original) (raw)
Инъективность
Инъективность
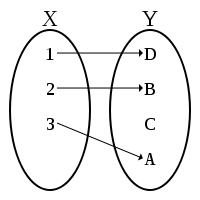
Инъективная функция.
Отображение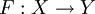 называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.
называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.
Формально это значит, что если два образа совпадают, то совпадают и прообразы (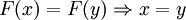 ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть 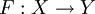 инъективно, если существует
инъективно, если существует 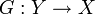 такое, что
такое, что 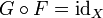 .
.
Примеры
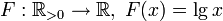 — инъективно.
— инъективно.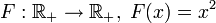 — инъективно.
— инъективно.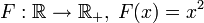 — не является инъективным (F( - 2) = F(2) = 4).
— не является инъективным (F( - 2) = F(2) = 4).
См. также
Литература
- Н. К. Верещагин, А.Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004—336 с.
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Инъективность" в других словарях:
- Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
- ГАЛУА КОГОМОЛОГИИ — когомологии Галуа группы. Если М абелева группа и группа Галуа расширения , действующая на М, то когомологии Галуа есть группы когомологии определяемые комплексом состоит из всех отображений , a d кограничный оператор (см. Когомологии групп).… … Математическая энциклопедия
- ИНЪЕКТИВНЫЙ МОДУЛЬ — инъективный объект в категории модулей над кольцом R, т. е. такой R модуль Енад ассоциативным кольцом R с единицей, что для любых R модулей М, N, для любого мономорфизма i: и для любого гомоморфизма f: найдется такой гомоморфизм g: что диаграмма… … Математическая энциклопедия
- КАТЕГОРИЯ — понятие, выделяющее ряд алгебраич. свойств совокупностей морфизмов однотипных математич. объектов (множеств, топологич. пространств, групп и т. п.) друг в друга при условии, что эти совокупности содержат тождественные отображения и замкнуты… … Математическая энциклопедия
- ПОЛИГОН — над моноидом R, R полигон, операнд, непустое множество с моноидом операторов. Точнее, непустое множество Аназ. левым П. над моноидом К, если для любых и определено произведение , причем и 1а=а для любых . Правый П. определяется аналогично.… … Математическая энциклопедия
- Биекция — Биективная функция. Биекция это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один … Википедия
- Булеан — Пусть множество. Множество всех подмножеств множества называется булеаном (также степенью множества (англ. power set), показательным множеством или множеством частей) и обозначается . Также оно обозначается , так как оно соответствует … Википедия
- Инъекция (математика) — У этого термина существуют и другие значения, см. Инъекция (значения). Инъективная функция. Отображение … Википедия
- Функциональная зависимость — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
- Биективность — Биективная функция. Функция называется биекцией (и обозначается ), если она: Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами … Википедия