Иррациональные числа | это... Что такое Иррациональные числа? (original) (raw)

Иррациональные числа

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби 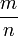$\frac{m}{n}$ , где m — целое число, n — натуральное число. 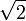О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа $\sqrt 2$ .

Множество иррациональных чисел обычно обозначается 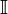$\mathbb I$ . Таким образом

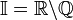
$\mathbb I =\R\backslash \Q$

— множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

Свойства

Всякое вещественное число может быть записано бесконечной десятичной дробью, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
Множество иррациональных чисел несчётно, является множеством второй категории.

Теоремы

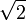$\sqrt{2}$ — иррациональное число

Допустим противное: 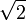$\sqrt{2}$ рационален, то есть представляется в виде несократимой дроби 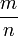$\frac{m}{n}$ , где m и n — целые числа. Возведём предполагаемое равенство в квадрат:

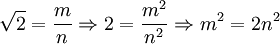$\sqrt{2} = \frac{m}{n} \Rightarrow 2 = \frac{m^2}{n^2} \Rightarrow m^2 = 2n^2$ .

Отсюда следует, что m_2 чётно, значит, чётно и m. Пускай m = 2_r, где r целое. Тогда

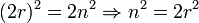
$(2r)^2=2n^2 \Rightarrow n^2=2r^2$

Следовательно, _n_2 чётно, значит, чётно и n. Мы получили, что m и n чётны, что противоречит несократимости дроби 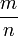$\frac{m}{n}$ . Значит, исходное предположение было неверным, и 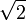$\sqrt{2}$ — иррациональное число.

log23 — иррациональное число

Допустим противное: log23 рационален, то есть представляется в виде дроби 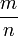$\frac{m}{n}$ , где m и n — целые числа. Поскольку log23 > 0, m и n могут быть выбраны положительными. Тогда

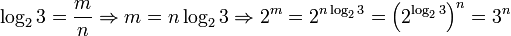
$\log_2 3 = \frac{m}{n} \Rightarrow m = n \log_2 3 \Rightarrow 2^m = 2^{n \log_2 3} = \left (2^{\log_2 3}\right )^n = 3^n$

Но 2_m_ чётно, а 3_n_ нечётно. Получаем противоречие.

e — иррациональное число

См. раздел «Доказательство иррациональности» в статье «e».

Другие иррациональные числа

Иррациональными являются:

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Иррациональные числа" в других словарях:

Числа с собственными именами — В этот список включены числа, имеющие собственные названия, не являющиеся стандартными сложносоставными названиями чисел. Именные названия степеней тысячи приводятся, только если у них есть иные названия. Содержание 1 Натуральные числа 1.1… … Википедия
Числа Кэли — Алгебра Кэли определённый тип гиперкомплексных чисел, 8 мерная алгебра над полем вещественных чисел. Обычно обозначается , поскольку её элементы (числа Кэли) называются иногда октонионами или октавами. Число Кэли это линейная комбинация… … Википедия
Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия
Вещественные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Действительные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Реальные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Двойные числа — О гиперкомплексных числах параболического типа см. дуальные числа Двойные числа или паракомплексные числа, расщепляемые комплексные числа, комплексные числа гиперболического типа гиперкомплексные числа вида « », где и вещественные… … Википедия
Дуальные числа — или (гипер)комплексные числа параболического типа гиперкомплексные числа вида , где и вещественные числа, и . Любое дуальное число однозначно определяется такой парой чисел и . Множество всех дуальных чисел образует двумерную коммутативную … Википедия
Супернатуральные числа — (иногда также именумые обобщённые натуральные числа или числа Стейница) являются обобщением натуральных чисел. Супернатуральное число является формальным произведением: где может быть любым простым числом, а каждое является или натуральным числом … Википедия
Кубические простые числа — Кубические простые числа это простые числа, которые являются решением одного из двух кубических уравнений третей степени от переменных x и y. Первое из них: [1] и первые несколько таких кубических простых чисел: 7, 19, 37, 61, 127, 271, 331 … Википедия