Криптографическая система с открытым ключом | это... Что такое Криптографическая система с открытым ключом? (original) (raw)
Криптографическая система с открытым ключом (или Асимметричное шифрование, Асимметричный шифр) — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифрования сообщения используется секретный ключ. [1] Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах SSL (лежащих в основе SSH. Также используется в S/MIME.
Содержание
- 1 Идея криптосистемы с открытым ключом
- 2 Схема шифрования с открытым ключом
- 3 Научная основа
- 4 Основные принципы построения криптосистем с открытым ключом
- 5 Криптография с несколькими открытыми ключами
- 6 Криптоанализ алгоритмов с открытым ключом
- 7 Особенности системы
- 8 Виды симметричных шифров
- 9 Виды асимметричных шифров
- 10 Примечания
- 11 См. также
- 12 Литература
Идея криптосистемы с открытым ключом
Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значение f(x), тогда как определение x из f(x) сложно в смысле теории.
Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой y, что зная f(x), можно вычислить x. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.
Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в компьютере. Каждый пользователь в сети имеет свой пароль. При входе, он указывает имя и вводит секретный пароль. Но если хранить пароль на диске компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции f(АЛИСАГЛАДИОЛУС), пусть результатом будет строка РОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:
| Имя | f(имя_пароль) |
|---|---|
| АЛИСА | РОМАШКА |
| БОБ | НАРЦИСС |
Вход в систему теперь выглядит так:
| Имя: | АЛИСА |
|---|---|
| Пароль: | ГЛАДИОЛУС |
Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к АЛИСАГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция необратимая.
В предыдущем примере используется односторонняя функция без лазейки, поскольку не требуется по зашифрованному сообщению получить исходное. В следующем примере рассматривается схема с возможностью восстановить исходное сообщение с помощью «лазейки», то есть труднодоступной информации. Для шифрования текста можно взять большой абонентский справочник, состоящий из нескольких толстых томов (по нему очень легко найти номер любого жителя города, но почти невозможно по известному номеру найти абонента). Для каждой буквы из шифруемого сообщения выбирается имя, начинающееся на ту же букву. Таким образом букве ставится в соответствие номер телефона абонента. Отправляемое сообщение, например «КОРОБКА», будет зашифровано следующим образом:
| Сообщение | Выбранное имя | Криптотекст |
|---|---|---|
| К | Королёв | 5643452 |
| О | Орехов | 3572651 |
| Р | Рузаева | 4673956 |
| O | Осипов | 3517289 |
| Б | Батурин | 7755628 |
| К | Кирсанова | 1235267 |
| А | Арсеньева | 8492746 |
Криптотекстом будет являться цепочка номеров, записанных в порядке их выбора в справочнике. Чтобы затруднить расшифровку, следует выбирать случайные имена, начинающиеся на нужную букву. Таким образом исходное сообщение может быть зашифровано множеством различных списков номеров (криптотекстов).
Примеры таких криптотекстов:
| Криптотекст 1 | Криптотекст 2 | Криптотекст 3 |
|---|---|---|
| 1235267 | 5643452 | 1235267 |
| 3572651 | 3517289 | 3517289 |
| 4673956 | 4673956 | 4673956 |
| 3517289 | 3572651 | 3572651 |
| 7755628 | 7755628 | 7755628 |
| 5643452 | 1235267 | 5643452 |
| 8492746 | 8492746 | 8492746 |
Чтобы расшифровать текст, надо иметь справочник, составленный согласно возрастанию номеров. Этот справочник является лазейкой (секрет, который помогает получить начальный текст), известной только легальным пользователям. Не имея на руках копии справочника, криптоаналитик затратит очень много времени на расшифровку.[2]
Схема шифрования с открытым ключом
Пусть K — пространство ключей, а e и d — ключи шифрования и расшифрования соответственно. E e — функция шифрования для произвольного ключа e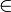 _K, такая что:
_K, такая что:
E e(m) = c
Здесь c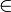 C, где C — пространство шифротекстов, а m
C, где C — пространство шифротекстов, а m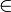 M, где M — пространство сообщений.
M, где M — пространство сообщений.
D d — функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифротекст c :
D d(c) = m
{E e: e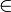 _K} — набор шифрования, а {D d: d
_K} — набор шифрования, а {D d: d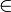 _K} — соответствующий набор для расшифрования. Каждая пара (E,D) имеет свойство: зная E e, невозможно решить уравнение E e(m) = c, то есть для данного произвольного шифротекста c
_K} — соответствующий набор для расшифрования. Каждая пара (E,D) имеет свойство: зная E e, невозможно решить уравнение E e(m) = c, то есть для данного произвольного шифротекста c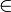 C, невозможно найти сообщение m
C, невозможно найти сообщение m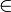 M. Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E e является односторонней функцией, а d — лазейкой.[3]
M. Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E e является односторонней функцией, а d — лазейкой.[3]
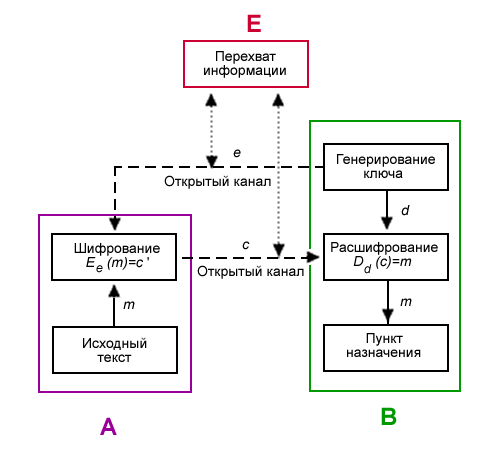
Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемых Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.
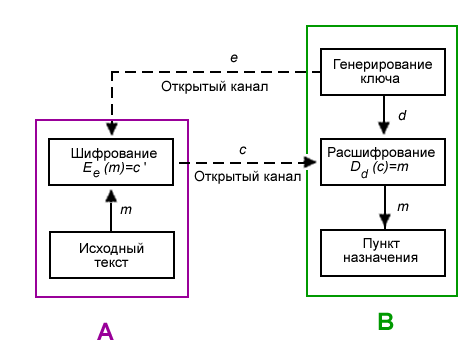
- Боб выбирает пару (e,d) и шлёт ключ шифрования e (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу, либо его подлинность должна быть гарантирована некоторым сертифицирующим органом).
- Чтобы послать сообщение m Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e: E e(m) = c, c — полученный шифротекст.
- Боб расшифровывает шифротекст c, применяя обратное преобразование D d, однозначно определённое значением d.
Научная основа
Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркле (Ralph Merkle) о распространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи-Хеллмана, был первым опубликованным практичным методом для установления разделения секретного ключа между заверенными пользователями канала. В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркле», признавая вклад Меркле в изобретение криптографии с открытым ключом. Эта же схема была разработана Малькольмом Вильямсоном в 1970-х, но держалась в секрете до 1997 года. Метод Меркле по распространению открытого ключа был изобретён в 1974 году и опубликован в 1978, его также называют загадкой Меркле.
В 1977 году учёными Рональдом Райвестом (Ronald Linn Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adleman) из Массачусетского Технологического Института (MIT) был разработан алгоритм шифрования, основанный на проблеме о разложении на множители. Система была названа по первым буквам их фамилий. Эта же система была изобретена Клиффордом Коксом (Clifford Cocks) в 1973 году, работавшим в центре правительственной связи (GCHQ). Но эта работа хранилась лишь во внутренних документах центра, поэтому о её существовании было не известно до 1977 года.
Вообще, в основу известных асимметричных криптосистем кладётся одна из сложных математических проблем, которая позволяет строить односторонние функции и функции-лазейки. Например, криптосистемы Меркля — Хеллмана и Хора — Ривеста опираются на так называемую задачу об укладке рюкзака.
Основные принципы построения криптосистем с открытым ключом
- Начинаем с трудной задачи P. Она должна решаться сложно в смысле теории: нет алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P за полиномиальное время относительно размера задачи.
- Можно выделить легкую подзадачу P' из P. Она должна решаться за полиномиальное время, лучше, если за линейное.
- «Перетасовываем и взбалтываем» P', чтобы получить задачу P'', совершенно не похожую на первоначальную. Задача P'', по крайней мере, должна выглядеть как оригинальная труднорешаемая задача P.
- P'' открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из P'' получить P', держится в секрете как секретная лазейка.
- Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как первый решает P'' задачу, второй использует секретную лазейку и решает P' задачу.
Криптография с несколькими открытыми ключами
- В следующем примере показана схема, в которой Алиса шифрует сообщение так, что только Боб может прочитать его, и наоборот, Боб шифрует сообщение так, что только Алиса может расшифровать его.
Пусть есть 3 ключа K A, K B, K C, распределенные так, как показано в таблице.
| Лицо | Ключ |
|---|---|
| Алиса | K A |
| Боб | K B |
| Кэрол | K C |
| Дэйв | K A, K B |
| Эллен | K B, K C |
| Франк | K A, K C |
Тогда Алиса может зашифровать сообщение ключом K A, а Эллен расшифровать ключами K B, K C, Кэрол — ключом K C, а Дэйв расшифровать ключами K A, K B. Если Дэйв зашифрует сообщение ключом K A, то сообщение сможет прочитать Эллен, если ключом K B, то его сможет прочитать Франк, если же обоими ключами K A и K B, то сообщение прочитает Кэрол. По аналогии действуют и другие участники. Таким образом, если используется одно подмножество ключей для шифрования, то для расшифрования требуются оставшиеся ключи множества. Такую схему можно использовать для n ключей.
| Шифруется ключом | Расшифровывается ключом |
|---|---|
| K B и K C | K A |
| K A и K C | K B |
| K A и K B | K C |
| K C | K A, K B |
| K A | K B, K C |
| K B | K A, K C |
- Теперь можно посылать сообщения группам агентов, не зная заранее состав группы.
Рассмотрим для начала множество, состоящее из трех агентов: Алисы, Боба и Кэрол. Алисе выдаются ключи K A и K B, Бобу — K B и K C, Кэрол — K A и K C. Теперь, если отправляемое сообщение зашифровано ключом K C, то его сможет прочитать только Алиса, последовательно применяя ключи K A и K B. Если нужно отправить сообщение Бобу, сообщение шифруется ключом K A, Кэрол — ключом K B. Если нужно отправить сообщение и Алисе и Кэрол, то для шифрования используются ключи K B и K C.
Преимущество этой схемы заключается в том, что для её реализации нужно только одно сообщение и n ключей (в схеме с n агентами). Если передаются индивидуальные сообщения, то есть используются отдельные ключи для каждого агента (всего n ключей) и каждого сообщения, то для передачи сообщений всем различным подмножествам требуется 2_n_ − 2 ключей.
Недостатком такой схемы является то, что необходимо также широковещательно передавать подмножество агентов (список имён может быть внушительным), которым нужно передать сообщение. Иначе каждому из них придется перебирать все комбинации ключей в поисках подходящей. Также агентам придется хранить немалый объём информации о ключах.[4]
Криптоанализ алгоритмов с открытым ключом
Казалось бы, что криптосистема с открытым ключом — идеальная система, не требующая безопасного канала для передачи ключа шифрования. Это подразумевало бы, что два легальных пользователя могли бы общаться по открытому каналу, не встречаясь, чтобы обменяться ключами. К сожалению, это не так. Рисунок иллюстрирует, как Ева, выполняющая роль активного перехватчика, может захватить систему (расшифровать сообщение, предназначенное Бобу) без взламывания системы шифрования.

В этой модели Ева перехватывает открытый ключ e, посланный Бобом Алисе. Затем создает пару ключей e' и d', «маскируется» под Боба, посылая Алисе открытый ключ e', который, как думает Алиса, открытый ключ, посланный ей Бобом. Ева перехватывает зашифрованные сообщения от Алисы к Бобу, расшифровывает их с помощью секретного ключа d', заново зашифровывает открытым ключом e Боба и отправляет сообщение Бобу. Таким образом, никто из участников не догадывается, что есть третье лицо, которое может как просто перехватить сообщение m, так и подменить его на ложное сообщение m'. Это подчеркивает необходимость аутентификации открытых ключей. Для этого обычно используют сертификаты. Распределённое управление ключами в [5]
Еще одна форма атаки — вычисление закрытого ключа, зная открытый (рисунок ниже). Криптоаналитик знает алгоритм шифрования E e, анализируя его, пытается найти D d. Этот процесс упрощается, если криптоаналитик перехватил несколько криптотекстов с, посланных лицом A лицу B.
Большинство криптосистем с открытым ключом основаны на проблеме факторизации больших чисел. К примеру,
| Год | Число десятичных разрядовв разложенном числе | Во сколько раз сложнее разложитьна множители 512-битовое число |
|---|---|---|
| 1983 | 71 | > 20 000 000 |
| 1985 | 80 | > 2 000 000 |
| 1988 | 90 | 250 000 |
| 1989 | 100 | 30 000 |
| 1993 | 120 | 500 |
| 1994 | 129 | 100 |
Также задачу разложения потенциально можно решить с помощью Алгоритма Шора при использовании достаточно мощного квантового компьютера.
Для многих методов несимметричного шифрования криптостойкость, полученная в результате криптоанализа, существенно отличается от величин, заявляемых разработчиками алгоритмов на основании теоретических оценок. Поэтому во многих странах вопрос применения алгоритмов шифрования данных находится в поле законодательного регулирования. В частности, в России к использованию в государственных и коммерческих организациях разрешены только те программные средства шифрования данных, которые прошли государственную сертификацию в административных органах, в частности, в ФСБ, ФСТЭК.[6]
Особенности системы
Применение
Алгоритмы криптосистемы с открытым ключом можно использовать[7]
- Как самостоятельные средства для защиты передаваемой и хранимой информации
- Как средства распределения ключей. Обычно с помощью алгоритмов криптосистем с открытым ключом распределяют ключи, малые по объёму. А саму передачу больших информационных потоков осуществляют с помощью других алгоритмов.
- Как средства аутентификации пользователей.
Преимущества
- Преимущество асимметричных шифров перед симметричными шифрами состоит в отсутствии необходимости предварительной передачи секретного ключа по надёжному каналу.
- В симметричной криптографии ключ держится в секрете для обеих сторон, а в асимметричной криптосистеме только один секретный.
- При симметричном шифровании необходимо обновлять ключ после каждого факта передачи, тогда как в асимметричных криптосистемах пару (E,D) можно не менять значительное время.
- В больших сетях число ключей в асимметричной криптосистеме значительно меньше, чем в симметричной.
Недостатки
- Преимущество алгоритма симметричного шифрования над несимметричным заключается в том, что в первый относительно легко внести изменения.
- Хотя сообщения надежно шифруются, но «засвечиваются» получатель и отправитель самим фактом пересылки шифрованного сообщения.[8]
- Несимметричные алгоритмы используют более длинные ключи, чем симметричные. Ниже приведена таблица, сопоставляющая длину ключа симметричного алгоритма с длиной ключа несимметричного алгоритма с аналогичной криптостойкостью:
| Длина симметричного ключа, бит | Длина несимметричного ключа, бит |
|---|---|
| 56 | 384 |
| 64 | 512 |
| 80 | 768 |
| 112 | 1792 |
| 128 | 2304 |
- Процесс шифрования-расшифрования с использованием пары ключей проходит на два-три порядка медленнее, чем шифрование-расшифрование того же текста симметричным алгоритмом.
- В чистом виде асимметричные криптосистемы требуют существенно больших вычислительных ресурсов, потому на практике используются в сочетании с другими алгоритмами.
- Для ЭЦП сообщение предварительно подвергается хешированию, а с помощью асимметричного ключа подписывается лишь относительно небольшой результат хеш-функции.
- Для шифрования они используются в форме гибридных криптосистем, где большие объёмы данных шифруются симметричным шифром на сеансовом ключе, а с помощью асимметричного шифра передаётся только сам сеансовый ключ.
Виды симметричных шифров
блочные шифры
- 3DES (Triple-DES, тройной DES)
- Ривеста (Rivest Cipher)) Twofish
- ГОСТ 28147-89
- IDEA (International Data Encryption Algorithm, интернациональный алгоритм шифрования данных)
- CAST (по инициалам разработчиков Carlisle Adams и Stafford Tavares)
- CRAB
потоковые шифры
- SEAL (Software Efficient Algorithm, программно-эффективный алгоритм)
Виды асимметричных шифров
- Elgamal (Шифросистема Эль-Гамаля)
- Diffie-Hellman (Обмен ключами Диффи — Хелмана)
- ECC (Elliptic Curve Cryptography, криптография эллиптической кривой)
- ГОСТ Р 34.10-2001
- Rabin
- Luc
- McEliece
Примечания
- ↑ Брюс Шнайер. Прикладная криптография. 2-е изд. Протоколы, алгоритмы и исходные тексты на языке Си. Глава 2.7 Цифровые подписи и шифрование.
- ↑ Саломаа А. Криптография с открытым ключом. с. 74-75
- ↑ Handbook of Applied Cryptography, Menezes A.J., Oorschot P.C., Vanstone S.A. С. 25—26
- ↑ Брюс Шнайер. Прикладная криптография. 2-е изд. Протоколы, алгоритмы и сиходные тексты на языке Си. Глава 3.5
- ↑ PGP. Распределение ключей..
- ↑ Принцип достаточной защиты.
- ↑ Баричев С. Криптография без секретов. с. 20
- ↑ См. например: Yoshiharu Maeno, Yukio Ohsawa. Discovering covert node in networked organization
См. также
Литература
- Саломаа А. Криптография с открытым ключом. — М.: Мир, 1995. — 318 с. — ISBN 5-03-001991-X
- A. J. Menezes, P. C. van Oorschot, S. A. Vanstone. Handbook of Applied Cryptography. — 1997. — ISBN 0-8493-8523-7
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4
Криптографические алгоритмы с парой открытый/закрытый ключ
Wikimedia Foundation.2010.