pymc.Beta — PyMC dev documentation (original) (raw)

class pymc.Beta(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#

Beta distribution.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}\]

where \(B\) is the Beta function.

For more information, see https://en.wikipedia.org/wiki/Beta_distribution.

(Source code, png, hires.png, pdf)

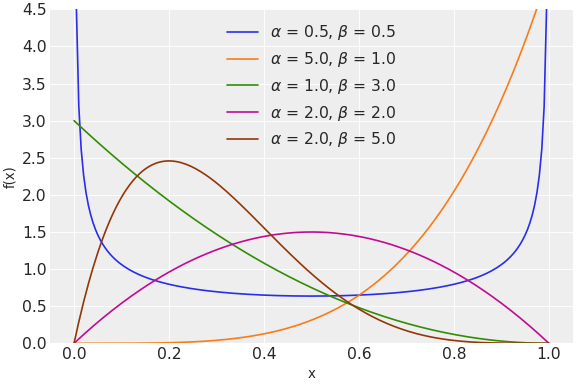
Beta distribution can be parameterized either in terms of alpha and beta, mean and standard deviation or mean and sample size. The link between the three parametrizations is given by

\[ \begin{align}\begin{aligned}\begin{split}\alpha &= \mu \kappa \\ \beta &= (1 - \mu) \kappa\end{split}\\\text{where } \kappa = \frac{\mu(1-\mu)}{\sigma^2} - 1\\\begin{split}\alpha &= \mu * \nu \\ \beta &= (1 - \mu) * \nu\end{split}\end{aligned}\end{align} \]

Parameters:

alphatensor_like of float, optional

alpha > 0. If not specified, then calculated using mu and sigma.

betatensor_like of float, optional

beta > 0. If not specified, then calculated using mu and sigma.

mutensor_like of float, optional

Alternative mean (0 < mu < 1).

sigmatensor_like of float, optional

Alternative standard deviation (0 < sigma < sqrt(mu * (1 - mu))).

nutensor_like of float, optional

Alternative “sample size” of a Beta distribution (nu > 0).

Notes

Beta distribution is a conjugate prior for the parameter \(p\) of the binomial distribution.

Methods