numpy.poly1d — NumPy v1.13 Manual (original) (raw)
class numpy. poly1d(c_or_r, r=False, variable=None)[source]¶
A one-dimensional polynomial class.
A convenience class, used to encapsulate “natural” operations on polynomials so that said operations may take on their customary form in code (see Examples).
| Parameters: | c_or_r : array_like The polynomial’s coefficients, in decreasing powers, or if the value of the second parameter is True, the polynomial’s roots (values where the polynomial evaluates to 0). For example,poly1d([1, 2, 3]) returns an object that represents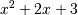 , whereas poly1d([1, 2, 3], True) returns one that represents , whereas poly1d([1, 2, 3], True) returns one that represents 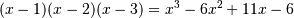 . r : bool, optional If True, c_or_r specifies the polynomial’s roots; the default is False. variable : str, optional Changes the variable used when printing p from x to variable(see Examples). . r : bool, optional If True, c_or_r specifies the polynomial’s roots; the default is False. variable : str, optional Changes the variable used when printing p from x to variable(see Examples). |
|---|
Examples
Construct the polynomial 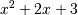 :
:
p = np.poly1d([1, 2, 3]) print(np.poly1d(p)) 2 1 x + 2 x + 3
Evaluate the polynomial at 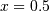 :
:
Find the roots:
p.r array([-1.+1.41421356j, -1.-1.41421356j]) p(p.r) array([ -4.44089210e-16+0.j, -4.44089210e-16+0.j])
These numbers in the previous line represent (0, 0) to machine precision
Show the coefficients:
Display the order (the leading zero-coefficients are removed):
Show the coefficient of the k-th power in the polynomial (which is equivalent to p.c[-(i+1)]):
Polynomials can be added, subtracted, multiplied, and divided (returns quotient and remainder):
p * p poly1d([ 1, 4, 10, 12, 9])
(p**3 + 4) / p (poly1d([ 1., 4., 10., 12., 9.]), poly1d([ 4.]))
asarray(p) gives the coefficient array, so polynomials can be used in all functions that accept arrays:
p**2 # square of polynomial poly1d([ 1, 4, 10, 12, 9])
np.square(p) # square of individual coefficients array([1, 4, 9])
The variable used in the string representation of p can be modified, using the variable parameter:
p = np.poly1d([1,2,3], variable='z') print(p) 2 1 z + 2 z + 3
Construct a polynomial from its roots:
np.poly1d([1, 2], True) poly1d([ 1, -3, 2])
This is the same polynomial as obtained by:
np.poly1d([1, -1]) * np.poly1d([1, -2]) poly1d([ 1, -3, 2])
Attributes
| c | A copy of the polynomial coefficients |
|---|---|
| coef | A copy of the polynomial coefficients |
| coefficients | A copy of the polynomial coefficients |
| coeffs | A copy of the polynomial coefficients |
| o | The order or degree of the polynomial |
| order | The order or degree of the polynomial |
| r | The roots of the polynomial, where self(x) == 0 |
| roots | The roots of the polynomial, where self(x) == 0 |
| variable | The name of the polynomial variable |
Methods
| __call__(val) | |
|---|---|
| deriv([m]) | Return a derivative of this polynomial. |
| integ([m, k]) | Return an antiderivative (indefinite integral) of this polynomial. |