numpy.polynomial.hermite.hermfromroots — NumPy v1.13 Manual (original) (raw)
numpy.polynomial.hermite. hermfromroots(roots)[source]¶
Generate a Hermite series with given roots.
The function returns the coefficients of the polynomial
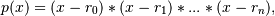
in Hermite form, where the r_n are the roots specified in roots. If a zero has multiplicity n, then it must appear in roots n times. For instance, if 2 is a root of multiplicity three and 3 is a root of multiplicity 2, then roots looks something like [2, 2, 2, 3, 3]. The roots can appear in any order.
If the returned coefficients are c, then
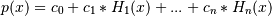
The coefficient of the last term is not generally 1 for monic polynomials in Hermite form.
| Parameters: | roots : array_like Sequence containing the roots. |
|---|---|
| Returns: | out : ndarray 1-D array of coefficients. If all roots are real then out is a real array, if some of the roots are complex, then out is complex even if all the coefficients in the result are real (see Examples below). |
See also
polyfromroots, legfromroots, lagfromroots, chebfromroots, hermefromroots.
Examples
from numpy.polynomial.hermite import hermfromroots, hermval coef = hermfromroots((-1, 0, 1)) hermval((-1, 0, 1), coef) array([ 0., 0., 0.]) coef = hermfromroots((-1j, 1j)) hermval((-1j, 1j), coef) array([ 0.+0.j, 0.+0.j])