numpy.random.triangular — NumPy v1.16 Manual (original) (raw)
numpy.random. triangular(left, mode, right, size=None)¶
Draw samples from the triangular distribution over the interval [left, right].
The triangular distribution is a continuous probability distribution with lower limit left, peak at mode, and upper limit right. Unlike the other distributions, these parameters directly define the shape of the pdf.
| Parameters: | left : float or array_like of floats Lower limit. mode : float or array_like of floats The value where the peak of the distribution occurs. The value should fulfill the condition left <= mode <= right. right : float or array_like of floats Upper limit, should be larger than left. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., (m, n, k), thenm * n * k samples are drawn. If size is None (default), a single value is returned if left, mode, and rightare all scalars. Otherwise, np.broadcast(left, mode, right).sizesamples are drawn. |
|---|---|
| Returns: | out : ndarray or scalar Drawn samples from the parameterized triangular distribution. |
Notes
The probability density function for the triangular distribution is
The triangular distribution is often used in ill-defined problems where the underlying distribution is not known, but some knowledge of the limits and mode exists. Often it is used in simulations.
References
| [1] | Wikipedia, “Triangular distribution”https://en.wikipedia.org/wiki/Triangular_distribution |
|---|
Examples
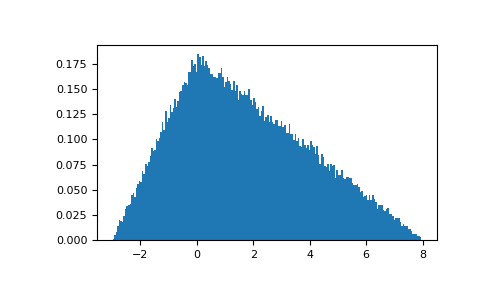
Draw values from the distribution and plot the histogram:
import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-3, 0, 8, 100000), bins=200, ... density=True) plt.show()