RectSphereBivariateSpline — SciPy v1.15.2 Manual (original) (raw)
scipy.interpolate.
class scipy.interpolate.RectSphereBivariateSpline(u, v, r, s=0.0, pole_continuity=False, pole_values=None, pole_exact=False, pole_flat=False)[source]#
Bivariate spline approximation over a rectangular mesh on a sphere.
Can be used for smoothing data.
Added in version 0.11.0.
Parameters:
uarray_like
1-D array of colatitude coordinates in strictly ascending order. Coordinates must be given in radians and lie within the open interval(0, pi).
varray_like
1-D array of longitude coordinates in strictly ascending order. Coordinates must be given in radians. First element (v[0]) must lie within the interval [-pi, pi). Last element (v[-1]) must satisfyv[-1] <= v[0] + 2*pi.
rarray_like
2-D array of data with shape (u.size, v.size).
sfloat, optional
Positive smoothing factor defined for estimation condition (s=0 is for interpolation).
pole_continuitybool or (bool, bool), optional
Order of continuity at the poles u=0 (pole_continuity[0]) andu=pi (pole_continuity[1]). The order of continuity at the pole will be 1 or 0 when this is True or False, respectively. Defaults to False.
pole_valuesfloat or (float, float), optional
Data values at the poles u=0 and u=pi. Either the whole parameter or each individual element can be None. Defaults to None.
pole_exactbool or (bool, bool), optional
Data value exactness at the poles u=0 and u=pi. If True, the value is considered to be the right function value, and it will be fitted exactly. If False, the value will be considered to be a data value just like the other data values. Defaults to False.
pole_flatbool or (bool, bool), optional
For the poles at u=0 and u=pi, specify whether or not the approximation has vanishing derivatives. Defaults to False.
Notes
Currently, only the smoothing spline approximation (iopt[0] = 0 andiopt[0] = 1 in the FITPACK routine) is supported. The exact least-squares spline approximation is not implemented yet.
When actually performing the interpolation, the requested v values must lie within the same length 2pi interval that the original v values were chosen from.
For more information, see the FITPACK site about this function.
Examples
Suppose we have global data on a coarse grid
import numpy as np lats = np.linspace(10, 170, 9) * np.pi / 180. lons = np.linspace(0, 350, 18) * np.pi / 180. data = np.dot(np.atleast_2d(90. - np.linspace(-80., 80., 18)).T, ... np.atleast_2d(180. - np.abs(np.linspace(0., 350., 9)))).T
We want to interpolate it to a global one-degree grid
new_lats = np.linspace(1, 180, 180) * np.pi / 180 new_lons = np.linspace(1, 360, 360) * np.pi / 180 new_lats, new_lons = np.meshgrid(new_lats, new_lons)
We need to set up the interpolator object
from scipy.interpolate import RectSphereBivariateSpline lut = RectSphereBivariateSpline(lats, lons, data)
Finally we interpolate the data. The RectSphereBivariateSpline object only takes 1-D arrays as input, therefore we need to do some reshaping.
data_interp = lut.ev(new_lats.ravel(), ... new_lons.ravel()).reshape((360, 180)).T
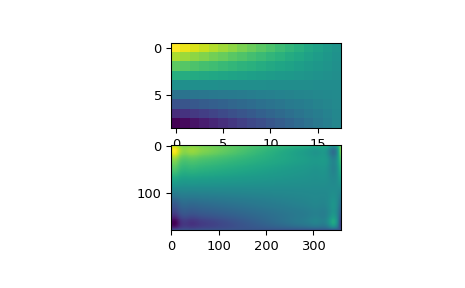
Looking at the original and the interpolated data, one can see that the interpolant reproduces the original data very well:
import matplotlib.pyplot as plt fig = plt.figure() ax1 = fig.add_subplot(211) ax1.imshow(data, interpolation='nearest') ax2 = fig.add_subplot(212) ax2.imshow(data_interp, interpolation='nearest') plt.show()
Choosing the optimal value of s can be a delicate task. Recommended values for s depend on the accuracy of the data values. If the user has an idea of the statistical errors on the data, she can also find a proper estimate for s. By assuming that, if she specifies the right s, the interpolator will use a spline f(u,v) which exactly reproduces the function underlying the data, she can evaluatesum((r(i,j)-s(u(i),v(j)))**2) to find a good estimate for this s. For example, if she knows that the statistical errors on herr(i,j)-values are not greater than 0.1, she may expect that a goods should have a value not larger than u.size * v.size * (0.1)**2.
If nothing is known about the statistical error in r(i,j), s must be determined by trial and error. The best is then to start with a very large value of s (to determine the least-squares polynomial and the corresponding upper bound fp0 for s) and then to progressively decrease the value of s (say by a factor 10 in the beginning, i.e.s = fp0 / 10, fp0 / 100, ... and more carefully as the approximation shows more detail) to obtain closer fits.
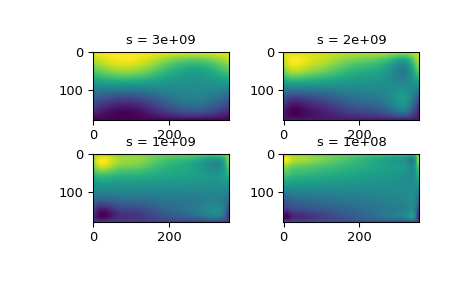
The interpolation results for different values of s give some insight into this process:
fig2 = plt.figure() s = [3e9, 2e9, 1e9, 1e8] for idx, sval in enumerate(s, 1): ... lut = RectSphereBivariateSpline(lats, lons, data, s=sval) ... data_interp = lut.ev(new_lats.ravel(), ... new_lons.ravel()).reshape((360, 180)).T ... ax = fig2.add_subplot(2, 2, idx) ... ax.imshow(data_interp, interpolation='nearest') ... ax.set_title(f"s = {sval:g}") plt.show()
Methods
| __call__(theta, phi[, dtheta, dphi, grid]) | Evaluate the spline or its derivatives at given positions. |
|---|---|
| ev(theta, phi[, dtheta, dphi]) | Evaluate the spline at points |
| get_coeffs() | Return spline coefficients. |
| get_knots() | Return a tuple (tx,ty) where tx,ty contain knots positions of the spline with respect to x-, y-variable, respectively. |
| get_residual() | Return weighted sum of squared residuals of the spline approximation: sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0) |
| partial_derivative(dx, dy) | Construct a new spline representing a partial derivative of this spline. |