freqresp — SciPy v1.15.3 Manual (original) (raw)

scipy.signal.

scipy.signal.freqresp(system, w=None, n=10000)[source]#

Calculate the frequency response of a continuous-time system.

Parameters:

systeman instance of the lti class or a tuple describing the system.

The following gives the number of elements in the tuple and the interpretation:

• 1 (instance of lti)
• 2 (num, den)
• 3 (zeros, poles, gain)
• 4 (A, B, C, D)

warray_like, optional

Array of frequencies (in rad/s). Magnitude and phase data is calculated for every value in this array. If not given, a reasonable set will be calculated.

nint, optional

Number of frequency points to compute if w is not given. The _n_frequencies are logarithmically spaced in an interval chosen to include the influence of the poles and zeros of the system.

Returns:

w1D ndarray

Frequency array [rad/s]

H1D ndarray

Array of complex magnitude values

Notes

If (num, den) is passed in for system, coefficients for both the numerator and denominator should be specified in descending exponent order (e.g. s^2 + 3s + 5 would be represented as [1, 3, 5]).

Examples

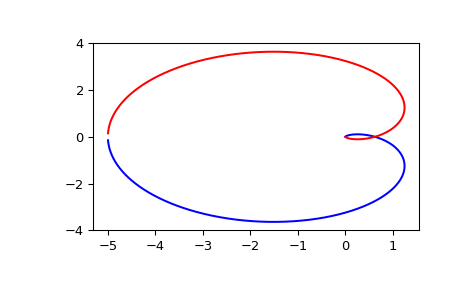
Generating the Nyquist plot of a transfer function

from scipy import signal import matplotlib.pyplot as plt

Construct the transfer function \(H(s) = \frac{5}{(s-1)^3}\):

s1 = signal.ZerosPolesGain([], [1, 1, 1], [5])

w, H = signal.freqresp(s1)

plt.figure() plt.plot(H.real, H.imag, "b") plt.plot(H.real, -H.imag, "r") plt.show()