lfilter — SciPy v1.15.3 Manual (original) (raw)

scipy.signal.

scipy.signal.lfilter(b, a, x, axis=-1, zi=None)[source]#

Filter data along one-dimension with an IIR or FIR filter.

Filter a data sequence, x, using a digital filter. This works for many fundamental data types (including Object type). The filter is a direct form II transposed implementation of the standard difference equation (see Notes).

The function sosfilt (and filter design using output='sos') should be preferred over lfilter for most filtering tasks, as second-order sections have fewer numerical problems.

Parameters:

barray_like

The numerator coefficient vector in a 1-D sequence.

aarray_like

The denominator coefficient vector in a 1-D sequence. If a[0]is not 1, then both a and b are normalized by a[0].

xarray_like

An N-dimensional input array.

axisint, optional

The axis of the input data array along which to apply the linear filter. The filter is applied to each subarray along this axis. Default is -1.

ziarray_like, optional

Initial conditions for the filter delays. It is a vector (or array of vectors for an N-dimensional input) of lengthmax(len(a), len(b)) - 1. If zi is None or is not given then initial rest is assumed. See lfiltic for more information.

Returns:

yarray

The output of the digital filter.

zfarray, optional

If zi is None, this is not returned, otherwise, zf holds the final filter delay values.

See also

lfiltic

Construct initial conditions for lfilter.

lfilter_zi

Compute initial state (steady state of step response) for lfilter.

filtfilt

A forward-backward filter, to obtain a filter with zero phase.

savgol_filter

A Savitzky-Golay filter.

sosfilt

Filter data using cascaded second-order sections.

sosfiltfilt

A forward-backward filter using second-order sections.

Notes

The filter function is implemented as a direct II transposed structure. This means that the filter implements:

a[0]*y[n] = b[0]*x[n] + b[1]*x[n-1] + ... + b[M]*x[n-M] - a[1]*y[n-1] - ... - a[N]*y[n-N]

where M is the degree of the numerator, N is the degree of the denominator, and n is the sample number. It is implemented using the following difference equations (assuming M = N):

a[0]*y[n] = b[0] * x[n] + d[0][n-1] d[0][n] = b[1] * x[n] - a[1] * y[n] + d[1][n-1] d[1][n] = b[2] * x[n] - a[2] * y[n] + d[2][n-1] ... d[N-2][n] = b[N-1]*x[n] - a[N-1]*y[n] + d[N-1][n-1] d[N-1][n] = b[N] * x[n] - a[N] * y[n]

where d are the state variables.

The rational transfer function describing this filter in the z-transform domain is:

                -1              -M
    b[0] + b[1]z  + ... + b[M] z

Y(z) = -------------------------------- X(z) -1 -N a[0] + a[1]z + ... + a[N] z

Examples

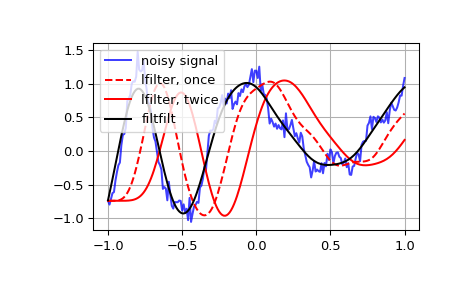
Generate a noisy signal to be filtered:

import numpy as np from scipy import signal import matplotlib.pyplot as plt rng = np.random.default_rng() t = np.linspace(-1, 1, 201) x = (np.sin(2np.pi0.75t(1-t) + 2.1) + ... 0.1np.sin(2np.pi1.25t + 1) + ... 0.18np.cos(2np.pi3.85t)) xn = x + rng.standard_normal(len(t)) * 0.08

Create an order 3 lowpass butterworth filter:

b, a = signal.butter(3, 0.05)

Apply the filter to xn. Use lfilter_zi to choose the initial condition of the filter:

zi = signal.lfilter_zi(b, a) z, _ = signal.lfilter(b, a, xn, zi=zi*xn[0])

Apply the filter again, to have a result filtered at an order the same as filtfilt:

z2, _ = signal.lfilter(b, a, z, zi=zi*z[0])

Use filtfilt to apply the filter:

y = signal.filtfilt(b, a, xn)

Plot the original signal and the various filtered versions:

plt.figure plt.plot(t, xn, 'b', alpha=0.75) plt.plot(t, z, 'r--', t, z2, 'r', t, y, 'k') plt.legend(('noisy signal', 'lfilter, once', 'lfilter, twice', ... 'filtfilt'), loc='best') plt.grid(True) plt.show()