scipy.special.airye — SciPy v1.15.2 Manual (original) (raw)

scipy.special.airye(z, out=None) = <ufunc 'airye'>#

Exponentially scaled Airy functions and their derivatives.

Scaling:

eAi = Ai * exp(2.0/3.0zsqrt(z)) eAip = Aip * exp(2.0/3.0zsqrt(z)) eBi = Bi * exp(-abs(2.0/3.0*(zsqrt(z)).real)) eBip = Bip * exp(-abs(2.0/3.0(z*sqrt(z)).real))

Parameters:

zarray_like

Real or complex argument.

outtuple of ndarray, optional

Optional output arrays for the function values

Returns:

eAi, eAip, eBi, eBip4-tuple of scalar or ndarray

Exponentially scaled Airy functions eAi and eBi, and their derivatives eAip and eBip

Notes

Wrapper for the AMOS [1] routines zairy and zbiry.

References

[1]

Donald E. Amos, “AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order”,http://netlib.org/amos/

Examples

We can compute exponentially scaled Airy functions and their derivatives:

import numpy as np from scipy.special import airye import matplotlib.pyplot as plt z = np.linspace(0, 50, 500) eAi, eAip, eBi, eBip = airye(z) f, ax = plt.subplots(2, 1, sharex=True) for ind, data in enumerate([[eAi, eAip, ["eAi", "eAip"]], ... [eBi, eBip, ["eBi", "eBip"]]]): ... ax[ind].plot(z, data[0], "-r", z, data[1], "-b") ... ax[ind].legend(data[2]) ... ax[ind].grid(True) plt.show()

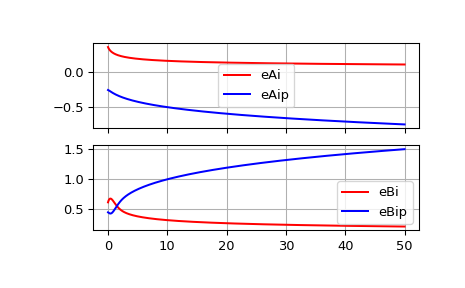
We can compute these using usual non-scaled Airy functions by:

from scipy.special import airy Ai, Aip, Bi, Bip = airy(z) np.allclose(eAi, Ai * np.exp(2.0 / 3.0 * z * np.sqrt(z))) True np.allclose(eAip, Aip * np.exp(2.0 / 3.0 * z * np.sqrt(z))) True np.allclose(eBi, Bi * np.exp(-abs(np.real(2.0 / 3.0 * z * np.sqrt(z))))) True np.allclose(eBip, Bip * np.exp(-abs(np.real(2.0 / 3.0 * z * np.sqrt(z))))) True

Comparing non-scaled and exponentially scaled ones, the usual non-scaled function quickly underflows for large values, whereas the exponentially scaled function does not.

airy(200) (0.0, 0.0, nan, nan) airye(200) (0.07501041684381093, -1.0609012305109042, 0.15003188417418148, 2.1215836725571093)