scipy.special.besselpoly — SciPy v1.15.2 Manual (original) (raw)

scipy.special.besselpoly(a, lmb, nu, out=None) = <ufunc 'besselpoly'>#

Weighted integral of the Bessel function of the first kind.

Computes

\[\int_0^1 x^\lambda J_\nu(2 a x) \, dx\]

where \(J_\nu\) is a Bessel function and \(\lambda=lmb\),\(\nu=nu\).

Parameters:

aarray_like

Scale factor inside the Bessel function.

lmbarray_like

Power of x

nuarray_like

Order of the Bessel function.

outndarray, optional

Optional output array for the function results.

Returns:

scalar or ndarray

Value of the integral.

References

Examples

Evaluate the function for one parameter set.

from scipy.special import besselpoly besselpoly(1, 1, 1) 0.24449718372863877

Evaluate the function for different scale factors.

import numpy as np factors = np.array([0., 3., 6.]) besselpoly(factors, 1, 1) array([ 0. , -0.00549029, 0.00140174])

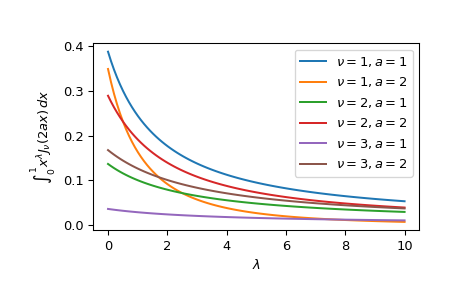
Plot the function for varying powers, orders and scales.

import matplotlib.pyplot as plt fig, ax = plt.subplots() powers = np.linspace(0, 10, 100) orders = [1, 2, 3] scales = [1, 2] all_combinations = [(order, scale) for order in orders ... for scale in scales] for order, scale in all_combinations: ... ax.plot(powers, besselpoly(scale, powers, order), ... label=rf"$\nu={order}, a={scale}$") ax.legend() ax.set_xlabel(r"$\lambda$") ax.set_ylabel(r"$\int_0^1 x^{\lambda} J_{\nu}(2ax),dx$") plt.show()