chebyu — SciPy v1.15.2 Manual (original) (raw)

scipy.special.

scipy.special.chebyu(n, monic=False)[source]#

Chebyshev polynomial of the second kind.

Defined to be the solution of

\[(1 - x^2)\frac{d^2}{dx^2}U_n - 3x\frac{d}{dx}U_n + n(n + 2)U_n = 0;\]

\(U_n\) is a polynomial of degree \(n\).

Parameters:

nint

Degree of the polynomial.

monicbool, optional

If True, scale the leading coefficient to be 1. Default is_False_.

Returns:

Uorthopoly1d

Chebyshev polynomial of the second kind.

See also

chebyt

Chebyshev polynomial of the first kind.

Notes

The polynomials \(U_n\) are orthogonal over \([-1, 1]\)with weight function \((1 - x^2)^{1/2}\).

References

[AS]

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Examples

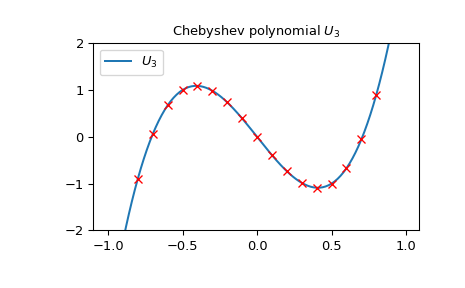
Chebyshev polynomials of the second kind of order \(n\) can be obtained as the determinant of specific \(n \times n\)matrices. As an example we can check how the points obtained from the determinant of the following \(3 \times 3\) matrix lay exactly on \(U_3\):

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import det from scipy.special import chebyu x = np.arange(-1.0, 1.0, 0.01) fig, ax = plt.subplots() ax.set_ylim(-2.0, 2.0) ax.set_title(r'Chebyshev polynomial U3U_3U3​') ax.plot(x, chebyu(3)(x), label=rf'$U_3$') for p in np.arange(-1.0, 1.0, 0.1): ... ax.plot(p, ... det(np.array([[2p, 1, 0], [1, 2p, 1], [0, 1, 2*p]])), ... 'rx') plt.legend(loc='best') plt.show()

They satisfy the recurrence relation:

\[U_{2n-1}(x) = 2 T_n(x)U_{n-1}(x)\]

where the \(T_n\) are the Chebyshev polynomial of the first kind. Let’s verify it for \(n = 2\):

from scipy.special import chebyt x = np.arange(-1.0, 1.0, 0.01) np.allclose(chebyu(3)(x), 2 * chebyt(2)(x) * chebyu(1)(x)) True

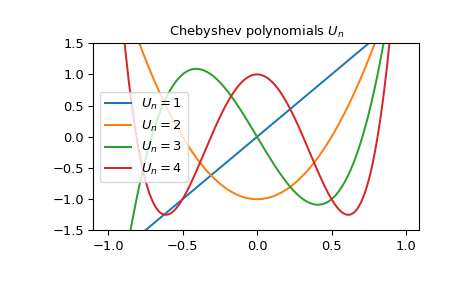
We can plot the Chebyshev polynomials \(U_n\) for some values of \(n\):

x = np.arange(-1.0, 1.0, 0.01) fig, ax = plt.subplots() ax.set_ylim(-1.5, 1.5) ax.set_title(r'Chebyshev polynomials UnU_nUn​') for n in np.arange(1,5): ... ax.plot(x, chebyu(n)(x), label=rf'$U_n={n}$') plt.legend(loc='best') plt.show()