scipy.special.gamma — SciPy v1.15.3 Manual (original) (raw)

scipy.special.gamma(z, out=None) = <ufunc 'gamma'>#

gamma function.

The gamma function is defined as

\[\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt\]

for \(\Re(z) > 0\) and is extended to the rest of the complex plane by analytic continuation. See [dlmf] for more details.

Parameters:

zarray_like

Real or complex valued argument

outndarray, optional

Optional output array for the function values

Returns:

scalar or ndarray

Values of the gamma function

Notes

The gamma function is often referred to as the generalized factorial since \(\Gamma(n + 1) = n!\) for natural numbers\(n\). More generally it satisfies the recurrence relation\(\Gamma(z + 1) = z \cdot \Gamma(z)\) for complex \(z\), which, combined with the fact that \(\Gamma(1) = 1\), implies the above identity for \(z = n\).

The gamma function has poles at non-negative integers and the sign of infinity as z approaches each pole depends upon the direction in which the pole is approached. For this reason, the consistent thing is for gamma(z) to return NaN at negative integers, and to return -inf when x = -0.0 and +inf when x = 0.0, using the signbit of zero to signify the direction in which the origin is being approached. This is for instance what is recommended for the gamma function in annex F entry 9.5.4 of the Iso C 99 standard [isoc99].

Prior to SciPy version 1.15, scipy.special.gamma(z) returned +infat each pole. This was fixed in version 1.15, but with the following consequence. Expressions where gamma appears in the denominator such as

gamma(u) * gamma(v) / (gamma(w) * gamma(x))

no longer evaluate to 0 if the numerator is well defined but there is a pole in the denominator. Instead such expressions evaluate to NaN. We recommend instead using the function rgamma for the reciprocal gamma function in such cases. The above expression could for instance be written as

gamma(u) * gamma(v) * (rgamma(w) * rgamma(x))

References

Examples

import numpy as np from scipy.special import gamma, factorial

gamma([0, 0.5, 1, 5]) array([ inf, 1.77245385, 1. , 24. ])

z = 2.5 + 1j gamma(z) (0.77476210455108352+0.70763120437959293j) gamma(z+1), z*gamma(z) # Recurrence property ((1.2292740569981171+2.5438401155000685j), (1.2292740569981158+2.5438401155000658j))

gamma(0.5)**2 # gamma(0.5) = sqrt(pi) 3.1415926535897927

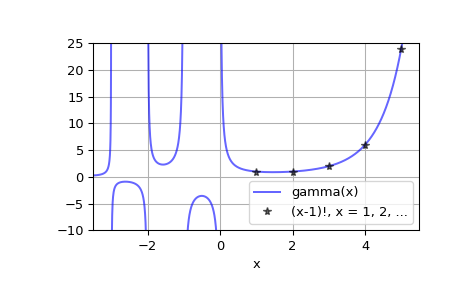
Plot gamma(x) for real x

x = np.linspace(-3.5, 5.5, 2251) y = gamma(x)

import matplotlib.pyplot as plt plt.plot(x, y, 'b', alpha=0.6, label='gamma(x)') k = np.arange(1, 7) plt.plot(k, factorial(k-1), 'k*', alpha=0.6, ... label='(x-1)!, x = 1, 2, ...') plt.xlim(-3.5, 5.5) plt.ylim(-10, 25) plt.grid() plt.xlabel('x') plt.legend(loc='lower right') plt.show()