scipy.special.i1 — SciPy v1.15.2 Manual (original) (raw)
scipy.special.i1(x, out=None) = <ufunc 'i1'>#
Modified Bessel function of order 1.
Defined as,
\[I_1(x) = \frac{1}{2}x \sum_{k=0}^\infty \frac{(x^2/4)^k}{k! (k + 1)!} = -\imath J_1(\imath x),\]
where \(J_1\) is the Bessel function of the first kind of order 1.
Parameters:
xarray_like
Argument (float)
outndarray, optional
Optional output array for the function values
Returns:
Iscalar or ndarray
Value of the modified Bessel function of order 1 at x.
See also
Modified Bessel function of the first kind
Exponentially scaled modified Bessel function of order 1
Notes
The range is partitioned into the two intervals [0, 8] and (8, infinity). Chebyshev polynomial expansions are employed in each interval.
This function is a wrapper for the Cephes [1] routine i1.
References
Examples
Calculate the function at one point:
from scipy.special import i1 i1(1.) 0.5651591039924851
Calculate the function at several points:
import numpy as np i1(np.array([-2., 0., 6.])) array([-1.59063685, 0. , 61.34193678])
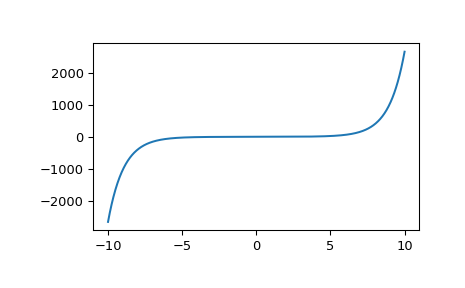
Plot the function between -10 and 10.
import matplotlib.pyplot as plt fig, ax = plt.subplots() x = np.linspace(-10., 10., 1000) y = i1(x) ax.plot(x, y) plt.show()