scipy.special.it2struve0 — SciPy v1.15.2 Manual (original) (raw)

scipy.special.it2struve0(x, out=None) = <ufunc 'it2struve0'>#

Integral related to the Struve function of order 0.

Returns the integral,

\[\int_x^\infty \frac{H_0(t)}{t}\,dt\]

where \(H_0\) is the Struve function of order 0.

Parameters:

xarray_like

Lower limit of integration.

outndarray, optional

Optional output array for the function values

Returns:

Iscalar or ndarray

The value of the integral.

Notes

Wrapper for a Fortran routine created by Shanjie Zhang and Jianming Jin [1].

References

Examples

Evaluate the function at one point.

import numpy as np from scipy.special import it2struve0 it2struve0(1.) 0.9571973506383524

Evaluate the function at several points by supplying an array for x.

points = np.array([1., 2., 3.5]) it2struve0(points) array([0.95719735, 0.46909296, 0.10366042])

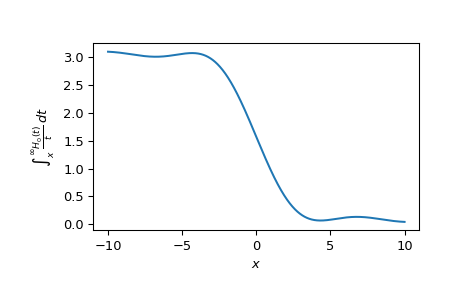
Plot the function from -10 to 10.

import matplotlib.pyplot as plt x = np.linspace(-10., 10., 1000) it2struve0_values = it2struve0(x) fig, ax = plt.subplots() ax.plot(x, it2struve0_values) ax.set_xlabel(r'$x$') ax.set_ylabel(r'$\int_x^{\infty}\frac{H_0(t)}{t},dt$') plt.show()