ivp — SciPy v1.15.2 Manual (original) (raw)

scipy.special.

scipy.special.ivp(v, z, n=1)[source]#

Compute derivatives of modified Bessel functions of the first kind.

Compute the nth derivative of the modified Bessel function _Iv_with respect to z.

Parameters:

varray_like or float

Order of Bessel function

zarray_like

Argument at which to evaluate the derivative; can be real or complex.

nint, default 1

Order of derivative. For 0, returns the Bessel function iv itself.

Returns:

scalar or ndarray

nth derivative of the modified Bessel function.

Notes

The derivative is computed using the relation DLFM 10.29.5 [2].

References

Examples

Compute the modified Bessel function of the first kind of order 0 and its first two derivatives at 1.

from scipy.special import ivp ivp(0, 1, 0), ivp(0, 1, 1), ivp(0, 1, 2) (1.2660658777520084, 0.565159103992485, 0.7009067737595233)

Compute the first derivative of the modified Bessel function of the first kind for several orders at 1 by providing an array for v.

ivp([0, 1, 2], 1, 1) array([0.5651591 , 0.70090677, 0.29366376])

Compute the first derivative of the modified Bessel function of the first kind of order 0 at several points by providing an array for z.

import numpy as np points = np.array([0., 1.5, 3.]) ivp(0, points, 1) array([0. , 0.98166643, 3.95337022])

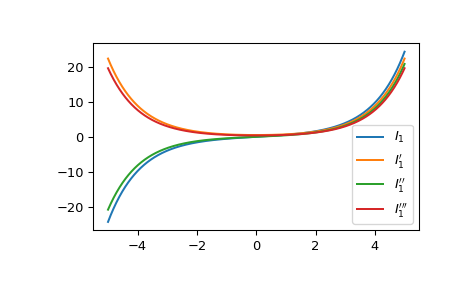
Plot the modified Bessel function of the first kind of order 1 and its first three derivatives.

import matplotlib.pyplot as plt x = np.linspace(-5, 5, 1000) fig, ax = plt.subplots() ax.plot(x, ivp(1, x, 0), label=r"$I_1$") ax.plot(x, ivp(1, x, 1), label=r"$I_1'$") ax.plot(x, ivp(1, x, 2), label=r"$I_1''$") ax.plot(x, ivp(1, x, 3), label=r"$I_1'''$") plt.legend() plt.show()