scipy.special.mathieu_sem — SciPy v1.15.2 Manual (original) (raw)

scipy.special.mathieu_sem(m, q, x, out=None) = <ufunc 'mathieu_sem'>#

Odd Mathieu function and its derivative

Returns the odd Mathieu function, se_m(x, q), of order m and parameter q evaluated at x (given in degrees). Also returns the derivative with respect to x of se_m(x, q).

Parameters:

marray_like

Order of the function

qarray_like

Parameter of the function

xarray_like

Argument of the function, given in degrees, not radians.

outtuple of ndarray, optional

Optional output arrays for the function results

Returns:

yscalar or ndarray

Value of the function

ypscalar or ndarray

Value of the derivative vs x

Notes

Odd Mathieu functions are the solutions to Mathieu’s differential equation

\[\frac{d^2y}{dx^2} + (b_m - 2q \cos(2x))y = 0\]

for which the characteristic number \(b_m\) (calculated with mathieu_b) results in an odd, periodic solution \(y(x)\) with period 180 degrees (for even \(m\)) or 360 degrees (for odd \(m\)).

References

Examples

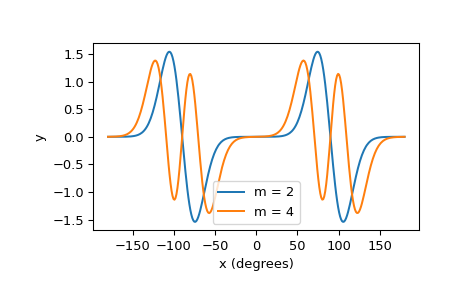
Plot odd Mathieu functions of orders 2 and 4.

import numpy as np from scipy import special import matplotlib.pyplot as plt m = np.asarray([2, 4]) q = 50 x = np.linspace(-180, 180, 300)[:, np.newaxis] y, _ = special.mathieu_sem(m, q, x) plt.plot(x, y) plt.xlabel('x (degrees)') plt.ylabel('y') plt.legend(('m = 2', 'm = 4'))

Because the orders 2 and4 are even, the period of each function is 180 degrees.