scipy.special.pseudo_huber — SciPy v1.15.2 Manual (original) (raw)

scipy.special.pseudo_huber(delta, r, out=None) = <ufunc 'pseudo_huber'>#

Pseudo-Huber loss function.

\[\mathrm{pseudo\_huber}(\delta, r) = \delta^2 \left( \sqrt{ 1 + \left( \frac{r}{\delta} \right)^2 } - 1 \right)\]

Parameters:

deltaarray_like

Input array, indicating the soft quadratic vs. linear loss changepoint.

rarray_like

Input array, possibly representing residuals.

outndarray, optional

Optional output array for the function results

Returns:

resscalar or ndarray

The computed Pseudo-Huber loss function values.

See also

huber

Similar function which this function approximates

Notes

Like huber, pseudo_huber often serves as a robust loss function in statistics or machine learning to reduce the influence of outliers. Unlike huber, pseudo_huber is smooth.

Typically, r represents residuals, the difference between a model prediction and data. Then, for \(|r|\leq\delta\),pseudo_huber resembles the squared error and for \(|r|>\delta\) the absolute error. This way, the Pseudo-Huber loss often achieves a fast convergence in model fitting for small residuals like the squared error loss function and still reduces the influence of outliers (\(|r|>\delta\)) like the absolute error loss. As \(\delta\) is the cutoff between squared and absolute error regimes, it has to be tuned carefully for each problem. pseudo_huber is also convex, making it suitable for gradient based optimization. [1] [2]

Added in version 0.15.0.

References

[1]

Hartley, Zisserman, “Multiple View Geometry in Computer Vision”. 2003. Cambridge University Press. p. 619

[2]

Charbonnier et al. “Deterministic edge-preserving regularization in computed imaging”. 1997. IEEE Trans. Image Processing. 6 (2): 298 - 311.

Examples

Import all necessary modules.

import numpy as np from scipy.special import pseudo_huber, huber import matplotlib.pyplot as plt

Calculate the function for delta=1 at r=2.

pseudo_huber(1., 2.) 1.2360679774997898

Calculate the function at r=2 for different delta by providing a list or NumPy array for delta.

pseudo_huber([1., 2., 4.], 3.) array([2.16227766, 3.21110255, 4. ])

Calculate the function for delta=1 at several points by providing a list or NumPy array for r.

pseudo_huber(2., np.array([1., 1.5, 3., 4.])) array([0.47213595, 1. , 3.21110255, 4.94427191])

The function can be calculated for different delta and r by providing arrays for both with compatible shapes for broadcasting.

r = np.array([1., 2.5, 8., 10.]) deltas = np.array([[1.], [5.], [9.]]) print(r.shape, deltas.shape) (4,) (3, 1)

pseudo_huber(deltas, r) array([[ 0.41421356, 1.6925824 , 7.06225775, 9.04987562], [ 0.49509757, 2.95084972, 22.16990566, 30.90169944], [ 0.49846624, 3.06693762, 27.37435121, 40.08261642]])

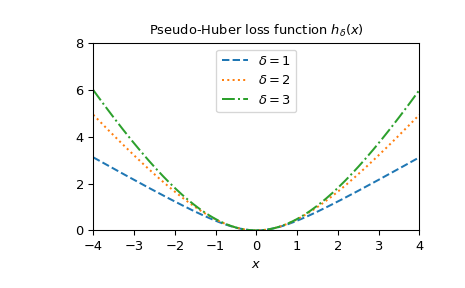
Plot the function for different delta.

x = np.linspace(-4, 4, 500) deltas = [1, 2, 3] linestyles = ["dashed", "dotted", "dashdot"] fig, ax = plt.subplots() combined_plot_parameters = list(zip(deltas, linestyles)) for delta, style in combined_plot_parameters: ... ax.plot(x, pseudo_huber(delta, x), label=rf"$\delta={delta}$", ... ls=style) ax.legend(loc="upper center") ax.set_xlabel("$x$") ax.set_title(r"Pseudo-Huber loss function hδ(x)h_{\delta}(x)hδ​(x)") ax.set_xlim(-4, 4) ax.set_ylim(0, 8) plt.show()

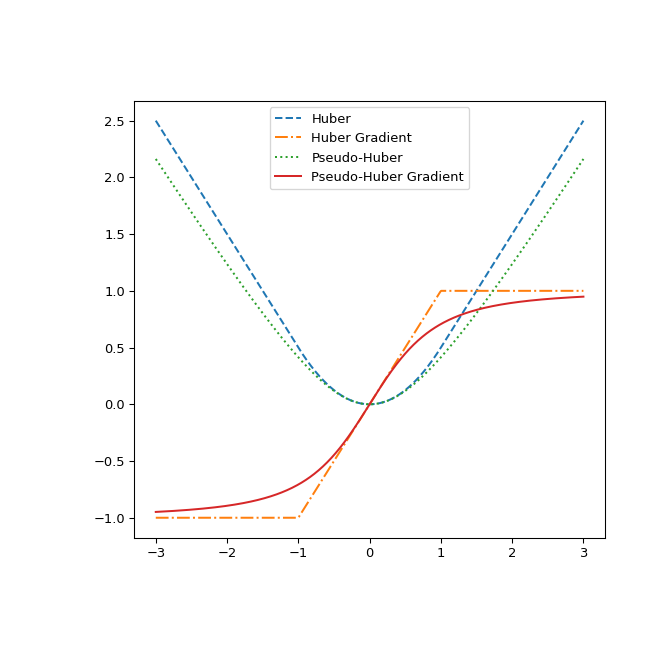
Finally, illustrate the difference between huber and pseudo_huber by plotting them and their gradients with respect to r. The plot shows that pseudo_huber is continuously differentiable while huber is not at the points \(\pm\delta\).

def huber_grad(delta, x): ... grad = np.copy(x) ... linear_area = np.argwhere(np.abs(x) > delta) ... grad[linear_area]=deltanp.sign(x[linear_area]) ... return grad def pseudo_huber_grad(delta, x): ... return x (1+(x/delta)2)(-0.5) x=np.linspace(-3, 3, 500) delta = 1. fig, ax = plt.subplots(figsize=(7, 7)) ax.plot(x, huber(delta, x), label="Huber", ls="dashed") ax.plot(x, huber_grad(delta, x), label="Huber Gradient", ls="dashdot") ax.plot(x, pseudo_huber(delta, x), label="Pseudo-Huber", ls="dotted") ax.plot(x, pseudo_huber_grad(delta, x), label="Pseudo-Huber Gradient", ... ls="solid") ax.legend(loc="upper center") plt.show()