spherical_in — SciPy v1.15.3 Manual (original) (raw)

scipy.special.

scipy.special.spherical_in(n, z, derivative=False)[source]#

Modified spherical Bessel function of the first kind or its derivative.

Defined as [1],

\[i_n(z) = \sqrt{\frac{\pi}{2z}} I_{n + 1/2}(z),\]

where \(I_n\) is the modified Bessel function of the first kind.

Parameters:

nint, array_like

Order of the Bessel function (n >= 0).

zcomplex or float, array_like

Argument of the Bessel function.

derivativebool, optional

If True, the value of the derivative (rather than the function itself) is returned.

Returns:

inndarray

Notes

The function is computed using its definitional relation to the modified cylindrical Bessel function of the first kind.

The derivative is computed using the relations [2],

\[ \begin{align}\begin{aligned}i_n' = i_{n-1} - \frac{n + 1}{z} i_n.\\i_1' = i_0\end{aligned}\end{align} \]

Added in version 0.18.0.

References

[AS]

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Examples

The modified spherical Bessel functions of the first kind \(i_n\)accept both real and complex second argument. They can return a complex type:

from scipy.special import spherical_in spherical_in(0, 3+5j) (-1.1689867793369182-1.2697305267234222j) type(spherical_in(0, 3+5j)) <class 'numpy.complex128'>

We can verify the relation for the derivative from the Notes for \(n=3\) in the interval \([1, 2]\):

import numpy as np x = np.arange(1.0, 2.0, 0.01) np.allclose(spherical_in(3, x, True), ... spherical_in(2, x) - 4/x * spherical_in(3, x)) True

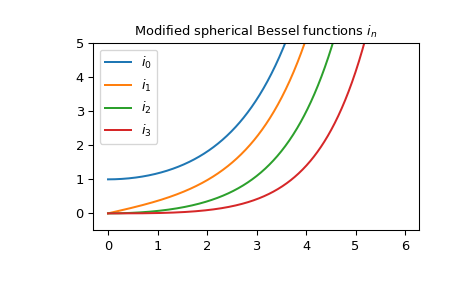
The first few \(i_n\) with real argument:

import matplotlib.pyplot as plt x = np.arange(0.0, 6.0, 0.01) fig, ax = plt.subplots() ax.set_ylim(-0.5, 5.0) ax.set_title(r'Modified spherical Bessel functions ini_nin​') for n in np.arange(0, 4): ... ax.plot(x, spherical_in(n, x), label=rf'$i_{n}$') plt.legend(loc='best') plt.show()