scipy.special.stdtr — SciPy v1.15.3 Manual (original) (raw)

scipy.special.stdtr(df, t, out=None) = <ufunc 'stdtr'>#

Student t distribution cumulative distribution function

Returns the integral:

\[\frac{\Gamma((df+1)/2)}{\sqrt{\pi df} \Gamma(df/2)} \int_{-\infty}^t (1+x^2/df)^{-(df+1)/2}\, dx\]

Parameters:

dfarray_like

Degrees of freedom

tarray_like

Upper bound of the integral

outndarray, optional

Optional output array for the function results

Returns:

scalar or ndarray

Value of the Student t CDF at t

Notes

The student t distribution is also available as scipy.stats.t. Calling stdtr directly can improve performance compared to thecdf method of scipy.stats.t (see last example below).

Examples

Calculate the function for df=3 at t=1.

import numpy as np from scipy.special import stdtr import matplotlib.pyplot as plt stdtr(3, 1) 0.8044988905221148

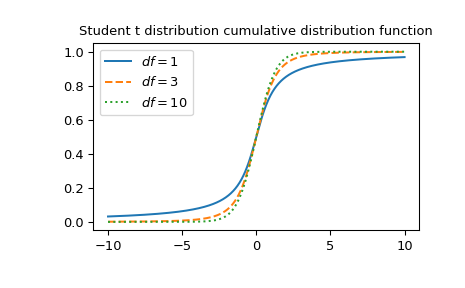
Plot the function for three different degrees of freedom.

x = np.linspace(-10, 10, 1000) fig, ax = plt.subplots() parameters = [(1, "solid"), (3, "dashed"), (10, "dotted")] for (df, linestyle) in parameters: ... ax.plot(x, stdtr(df, x), ls=linestyle, label=f"$df={df}$") ax.legend() ax.set_title("Student t distribution cumulative distribution function") plt.show()

The function can be computed for several degrees of freedom at the same time by providing a NumPy array or list for df:

stdtr([1, 2, 3], 1) array([0.75 , 0.78867513, 0.80449889])

It is possible to calculate the function at several points for several different degrees of freedom simultaneously by providing arrays for _df_and t with shapes compatible for broadcasting. Compute stdtr at 4 points for 3 degrees of freedom resulting in an array of shape 3x4.

dfs = np.array([[1], [2], [3]]) t = np.array([2, 4, 6, 8]) dfs.shape, t.shape ((3, 1), (4,))

stdtr(dfs, t) array([[0.85241638, 0.92202087, 0.94743154, 0.96041658], [0.90824829, 0.97140452, 0.98666426, 0.99236596], [0.93033702, 0.98599577, 0.99536364, 0.99796171]])

The t distribution is also available as scipy.stats.t. Calling stdtrdirectly can be much faster than calling the cdf method ofscipy.stats.t. To get the same results, one must use the following parametrization: scipy.stats.t(df).cdf(x) = stdtr(df, x).

from scipy.stats import t df, x = 3, 1 stdtr_result = stdtr(df, x) # this can be faster than below stats_result = t(df).cdf(x) stats_result == stdtr_result # test that results are equal True