ynp_zeros — SciPy v1.15.2 Manual (original) (raw)

scipy.special.

scipy.special.ynp_zeros(n, nt)[source]#

Compute zeros of integer-order Bessel function derivatives Yn’(x).

Compute nt zeros of the functions \(Y_n'(x)\) on the interval \((0, \infty)\). The zeros are returned in ascending order.

Parameters:

nint

Order of Bessel function

ntint

Number of zeros to return

Returns:

ndarray

First nt zeros of the Bessel derivative function.

References

Examples

Compute the first four roots of the first derivative of the Bessel function of second kind for order 0 \(Y_0'\).

from scipy.special import ynp_zeros ynp_zeros(0, 4) array([ 2.19714133, 5.42968104, 8.59600587, 11.74915483])

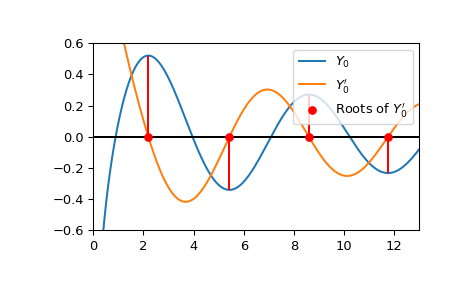
Plot \(Y_0\), \(Y_0'\) and confirm visually that the roots of\(Y_0'\) are located at local extrema of \(Y_0\).

import numpy as np import matplotlib.pyplot as plt from scipy.special import yn, ynp_zeros, yvp zeros = ynp_zeros(0, 4) xmax = 13 x = np.linspace(0, xmax, 500) fig, ax = plt.subplots() ax.plot(x, yn(0, x), label=r'$Y_0$') ax.plot(x, yvp(0, x, 1), label=r"$Y_0'$") ax.scatter(zeros, np.zeros((4, )), s=30, c='r', ... label=r"Roots of Y0′Y_0'Y0′​", zorder=5) for root in zeros: ... y0_extremum = yn(0, root) ... lower = min(0, y0_extremum) ... upper = max(0, y0_extremum) ... ax.vlines(root, lower, upper, color='r') ax.hlines(0, 0, xmax, color='k') ax.set_ylim(-0.6, 0.6) ax.set_xlim(0, xmax) plt.legend() plt.show()