ppcc_max — SciPy v1.15.3 Manual (original) (raw)

scipy.stats.

scipy.stats.ppcc_max(x, brack=(0.0, 1.0), dist='tukeylambda')[source]#

Calculate the shape parameter that maximizes the PPCC.

The probability plot correlation coefficient (PPCC) plot can be used to determine the optimal shape parameter for a one-parameter family of distributions. ppcc_max returns the shape parameter that would maximize the probability plot correlation coefficient for the given data to a one-parameter family of distributions.

Parameters:

xarray_like

Input array.

bracktuple, optional

Triple (a,b,c) where (a<b<c). If bracket consists of two numbers (a, c) then they are assumed to be a starting interval for a downhill bracket search (see scipy.optimize.brent).

diststr or stats.distributions instance, optional

Distribution or distribution function name. Objects that look enough like a stats.distributions instance (i.e. they have a ppf method) are also accepted. The default is 'tukeylambda'.

Returns:

shape_valuefloat

The shape parameter at which the probability plot correlation coefficient reaches its max value.

Notes

The brack keyword serves as a starting point which is useful in corner cases. One can use a plot to obtain a rough visual estimate of the location for the maximum to start the search near it.

References

[1]

J.J. Filliben, “The Probability Plot Correlation Coefficient Test for Normality”, Technometrics, Vol. 17, pp. 111-117, 1975.

Examples

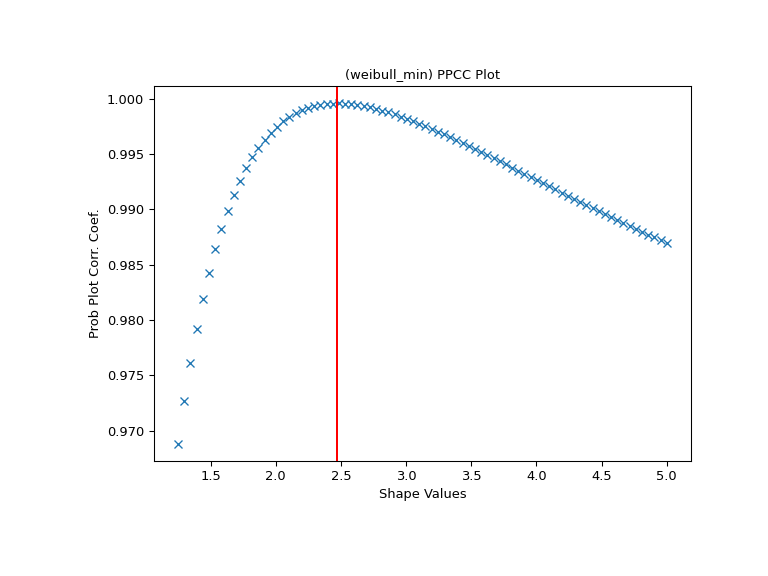
First we generate some random data from a Weibull distribution with shape parameter 2.5:

import numpy as np from scipy import stats import matplotlib.pyplot as plt rng = np.random.default_rng() c = 2.5 x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

Generate the PPCC plot for this data with the Weibull distribution.

fig, ax = plt.subplots(figsize=(8, 6)) res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax)

We calculate the value where the shape should reach its maximum and a red line is drawn there. The line should coincide with the highest point in the PPCC graph.

cmax = stats.ppcc_max(x, brack=(c/2, 2*c), dist='weibull_min') ax.axvline(cmax, color='r') plt.show()