Example: Line Fitting (original) (raw)

Next: Example: Plane Fitting Up: The Fast Hough Transform Previous: The FHT Algorithm Contents

Example: Line Fitting

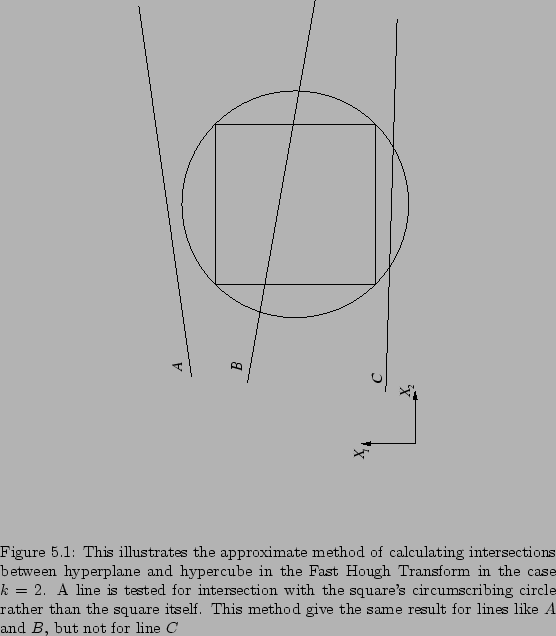
Figure 5.5shows how the FHT works for $k=2$ , when parameter space is a plane, hyperplanes are straight lines and hypercubes are squares whose associated hyperspheres are circles passing through the vertices of the squares (figure 5.5).

$\begin{figure} % latex2html id marker 5668 \centerline{\psfig{file=hyper.ps,wid... ...he same result for lines like <math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>A</mi></mrow><annotation encoding="application/x-tex">A</annotation></semantics></math>A and <math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B, but not for line <math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>C</mi></mrow><annotation encoding="application/x-tex">C</annotation></semantics></math>C} \end{figure}$

This is applicable to the problem of finding a straight line through points on a plane. If the plane has coordinates 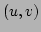$(u,v)$ the line can be written

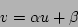
$\begin{displaymath} v=\alpha u + \beta \end{displaymath}$

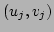where $\alpha$ and $\beta$ are constant. Each point $(u_j , v_j )$ votes for a line in parameter space:

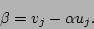
$\begin{displaymath} \beta=v_j - \alpha u_j . \end{displaymath}$

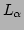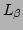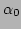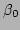Let the initial ranges of $\alpha$ and $\beta$ , defining the root hypercube, be $L_{\alpha}$ and $L_{\beta}$ centred around $\alpha_0$ and $\beta_0$ respectively. Then the above equation can put in the form of equation 5.15 using the transformation

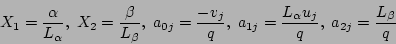
$\begin{displaymath} X_1 = \frac{\alpha}{L_\alpha} ,\; X_2 = \frac{\beta}{L_\be... ...{1j} = \frac{L_\alpha u_j}{q} ,\; a_{2j} = \frac{L_\beta}{q} \end{displaymath}$

where 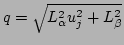$q = \sqrt{L_\alpha^2 u_j^2 + L_\beta^2}$ .

2006-03-17