Calculating the Intersection of a Plane and a Sphere (original) (raw)

Next: Calculating the Plane Parameters Up: Example: Plane Fitting Previous: Example: Plane Fitting Contents

Calculating the Intersection of a Plane and a Sphere

The perpendicular, and therefore nearest, distance from the plane to the centre of the cube is calculated. If it is smaller than the radius of the circumscribing sphere, the plane intersects the sphere, otherwise it misses. The distance is normalised by dividing it by the side length of the cube. The normalised distance of a plane from the centre of a child cube can be calculated simply from the normalised distance of the plane from it's parent's centre, as shown below. The plane is defined by the following equation:

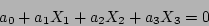
$\begin{displaymath} a_0 + a_1 X_1 + a_2 X_2 + a_3 X_3 = 0 \end{displaymath}$

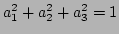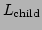where $a_1^2 + a_2^2 + a_3^2 = 1$ . Let the child cube have indices $[b_1, b_2, b_3]$ , centre $(C_1,C_2,C_3)$ and side length $L_{\rm child}$ . The radius of the circumscribing sphere is 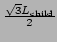$\frac{\sqrt{3} L_{\rm child}}{2}$ . The perpendicular distance of the plane to the centre of the child cube is

When normalised this becomes

$\begin{displaymath} R_{\rm child} = \frac{a_0 + a_1 C_1 + a_2 C_2 + a_3 C_3}{L_{\rm child}}. \end{displaymath}$	(5.16)

The normalised distance of the centre of the parent from the plane, where the parent has centre 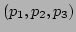$(p_1,p_2,p_3)$ and side length 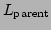$L_{\rm parent}$ , is

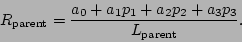
$\begin{displaymath} R_{\rm parent} = \frac{a_0 + a_1 p_1 + a_2 p_2 + a_3 p_3}{L_{\rm parent}}. \end{displaymath}$

The child is half the size of the parent, so $L_{\rm parent} = 2 L_{\rm child}$ . Also the centres of the cubes are related by the following equation:

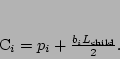$\begin{displaymath} C_i = p_i + \frac{b_i L_{\rm child}}{2}. \end{displaymath}$	(5.17)

and substituting the RHS into equation 5.16 yields

This formula is used to calculate the normalised distance for a child in terms of that of it's parent, and is fast because the 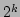$2^k$ values of the term 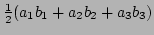$\frac{1}{2} (a_1 b_1 + a_2 b_2 + a_3 b_3)$ can be stored as a look-up table for each set of coefficients 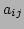$a_{ij}$ (i.e. each disparity point).

The normalised distance of the plane from the root cube, which has side length one and centre 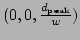$(0,0, \frac{d_{\rm peak}}{w})$ , is

$\begin{displaymath} R_{\rm root} = a_0 + a_3 \frac{d_{\rm peak}}{w}. \end{displaymath}$	(5.19)

The normalised distances are calculated initially from equation 5.19 and from then on using the formula 5.18. The normalised distances are compared with 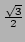$\frac{\sqrt{3}}{2}$ , the radius of the circumscribing sphere of a cube with side length one. This is equivalent to comparing the un-normalised distance with the circumscribing sphere of the original cube.

Next: Calculating the Plane Parameters Up: Example: Plane Fitting Previous: Example: Plane Fitting Contents

2006-03-17