Fixed size matrix/matrix multiplication (original) (raw)

Next: Fixed size matrix inverse Up: Fixed size matrices Previous: Fixed size matrix/vector multiplication Contents

Fixed size matrix/matrix multiplication

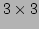Most useful matrix product combinations are supported by Gandalf. Here we describe all the combinations involving $3\times 4$ matrices. The first functions to describe are those which involve multiplication by a $3\times 3$ on the left or 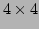$4\times 4$ matrix on the right, the square matrix optionally being (implicitly) transposed, the product producing another $3\times 4$ matrix. The operator combinations are

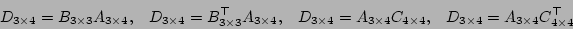
$\begin{displaymath}D_{3\times 4} = B_{3\times 3} A_{3\times 4},\;\;\; D_{3\time... ... 4},\;\;\; D_{3\times 4} = A_{3\times 4} C_{4\times 4}^{\top} \end{displaymath}$

which are implemented in Gandalf using the macros

  Gan_Matrix34 m34A, m34D;
  Gan_Matrix33 m33B;
  Gan_Matrix44 m44C;

  /* ... set up m34A, m33B and m44C ... */
  gan_mat34_lmultm33_q  ( &m34A, &m33B, &m34D ); /* D = B*A   */
  gan_mat34_lmultm33T_q ( &m34A, &m33B, &m34D ); /* D = B*A^T */
  gan_mat34_rmultm44_q  ( &m34A, &m44C, &m34D ); /* D = A*C   */
  gan_mat34_rmultm44T_q ( &m34A, &m44C, &m34D ); /* D = A*C^T */

Equivalent function calls are available:

  m34D = gan_mat34_lmultm33_s  ( &m34A, &m33B ); /* D = B*A   */
  m34D = gan_mat34_lmultm33T_s ( &m34A, &m33B ); /* D = B*A^T */
  m34D = gan_mat34_rmultm44_s  ( &m34A, &m44C ); /* D = A*C   */
  m34D = gan_mat34_rmultm44T_s ( &m34A, &m44C ); /* D = A*C^T */

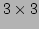Note that although by and large the functions described here for $3\times 4$ matrices are repeated for square matrices, there is redundancy because in the case of $3\times 3$ matrices the routines

  m33D = gan_mat33_lmultm33_s  ( &m33A, &m33B ); /* D = B*A   */
  m33D = gan_mat33_rmultm33_s  ( &m33B, &m33A ); /* D = B*A   */

would be equivalent, so in fact only the routinesgan_mat33_rmultm33_[qs]() are defined.

The square matrix may be symmetric or triangular, for which cases there are specific Gandalf functions. Firstly for multiplying by symmetric matrices we have the routines

  Gan_Matrix34 m34A, m34B;
  Gan_SquMatrix33 sm33S;
  Gan_SquMatrix44 sm44S;

  /* ... set up m34A, symmetric sm33S and sm44S ... */
  gan_mat34_lmults33_q ( &m34A, &sm33S, &m34B ); /* B = S*A, macro */
  gan_mat34_rmults44_q ( &m34A, &sm44S, &m34B ); /* B = A*S, macro */

with equivalent function calls

  m34B = gan_mat34_lmults33_q ( &m34A, &sm33S ); /* B = S*A, function call */
  m34B = gan_mat34_rmults44_q ( &m34A, &sm44S ); /* B = A*S, function call */

When multiplying by a triangular matrix, there are also options of implicit transpose and inverse, as described in the introduction to this chapter. Gandalf also supports in-place operations in this case. So there is a whole family of functions covering multiplication of a matrix by a triangular matrix. Mathematically the operations are

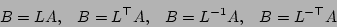
$\begin{displaymath}B=LA, \;\;\; B=L^{\top}A, \;\;\; B=L^{-1}A, \;\;\; B=L^{-\top}A \end{displaymath}$

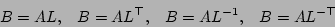
$\begin{displaymath}B=AL, \;\;\; B=AL^{\top}, \;\;\; B=AL^{-1}, \;\;\; B=AL^{-\top} \end{displaymath}$

Gandalf macro routines to implement these operations are

  Gan_Matrix34 m34A, m34B;
  Gan_SquMatrix33 sm33L;
  Gan_SquMatrix44 sm44L;

  /* ... set up m34A, lower triangular sm33L and sm44L ... */
  gan_mat34_lmultl33_q   ( &m34A, &sm33L, &m34B ); /* B = L*A,    macro */
  gan_mat34_lmultl33T_q  ( &m34A, &sm33L, &m34B ); /* B = L^T*A,  macro */
  gan_mat34_lmultl33I_q  ( &m34A, &sm33L, &m34B ); /* B = L^-1*A, macro */
  gan_mat34_lmultl33IT_q ( &m34A, &sm33L, &m34B ); /* B = L^-T*A, macro */
  gan_mat34_rmultl44_q   ( &m34A, &sm44L, &m34B ); /* B = A*L,    macro */
  gan_mat34_rmultl44T_q  ( &m34A, &sm44L, &m34B ); /* B = A*L^T,  macro */
  gan_mat34_rmultl44I_q  ( &m34A, &sm44L, &m34B ); /* B = A*L^-1, macro */
  gan_mat34_rmultl44IT_q ( &m34A, &sm44L, &m34B ); /* B = A*L^-T, macro */

There are also function calls to implement the same operations:

  m34B = gan_mat34_lmultl33_s   ( &m34A, &sm33L ); /* B = L*A,    function call */
  m34B = gan_mat34_lmultl33T_s  ( &m34A, &sm33L ); /* B = L^T*A,  function call */
  m34B = gan_mat34_lmultl33I_s  ( &m34A, &sm33L ); /* B = L^-1*A, function call */
  m34B = gan_mat34_lmultl33IT_s ( &m34A, &sm33L ); /* B = L^-T*A, function call */
  m34B = gan_mat34_rmultl44_s   ( &m34A, &sm44L ); /* B = A*L,    function call */
  m34B = gan_mat34_rmultl44T_s  ( &m34A, &sm44L ); /* B = A*L^T,  function call */
  m34B = gan_mat34_rmultl44I_s  ( &m34A, &sm44L ); /* B = A*L^-1, function call */
  m34B = gan_mat34_rmultl44IT_s ( &m34A, &sm44L ); /* B = A*L^-T, function call */

Finally there is a set of macros for writing the result in-place into the $3\times 4$ matrix $A$ .

  gan_mat34_lmultl33_i   ( &m34A, &sm33L ); /* A = L*A,    macro */
  gan_mat34_lmultl33T_i  ( &m34A, &sm33L ); /* A = L^T*A,  macro */
  gan_mat34_lmultl33I_i  ( &m34A, &sm33L ); /* A = L^-1*A, macro */
  gan_mat34_lmultl33IT_i ( &m34A, &sm33L ); /* A = L^-T*A, macro */
  gan_mat34_rmultl44_i   ( &m34A, &sm44L ); /* A = A*L,    macro */
  gan_mat34_rmultl44T_i  ( &m34A, &sm44L ); /* A = A*L^T,  macro */
  gan_mat34_rmultl44I_i  ( &m34A, &sm44L ); /* A = A*L^-1, macro */
  gan_mat34_rmultl44IT_i ( &m34A, &sm44L ); /* A = A*L^-T, macro */

The next set of functions deals with multiplying a matrix by itself in transpose, resulting in a symmetric matrix. These operations have the form

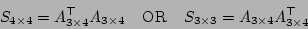
$\begin{displaymath}S_{4\times 4} = A_{3\times 4}^{\top}A_{3\times 4}\;\;\;\;\mbox{OR}\;\;\;\; S_{3\times 3} = A_{3\times 4} A_{3\times 4}^{\top} \end{displaymath}$

The Gandalf macro routines to implement these operations are

  Gan_Matrix34 m34A;
  Gan_SquMatrix33 sm33S;
  Gan_SquMatrix44 sm44S;

  /* ... set up m34A using e.g. gan_mat34_fill_q() ... */
  gan_mat34_slmultT_q ( &m34A, &sm44S ); /* S = A^T*A */
  gan_mat34_srmultT_q ( &m34A, &sm33S ); /* S = A*A^T */

with equivalent function calls

  sm44S = gan_mat34_slmultT_s ( &m34A ); /* S = A^T*A */
  sm33S = gan_mat34_srmultT_s ( &m34A ); /* S = A*A^T */

There are similar routines for general 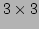$3\times 3$ matrices. For triangular matrices the functions are

  Gan_SquMatrix33 sm33L, sm33S;

  /* ... set up sm33L using e.g. gan_ltmat33_fill_q()... */
  gan_ltmat33_slmultT_q ( &sm33L, &sm33S ); /* S = L^T*L, macro */
  sm33S = gan_ltmat33_slmultT_s ( &sm33L ); /* S = L^T*L, function call */
  gan_ltmat33_srmultT_q ( &sm33L, &sm33S ); /* S = L*L^T, macro */
  sm33S = gan_ltmat33_srmultT_s ( &sm33L ); /* S = L*L^T, function call */

In the case of triangular matrices the operation ``multiply by transposed self'' can also be done in-place, so we also have the macro routines

  Gan_SquMatrix33 sm33A;

  /* ... set up sm33A as triangular using e.g. gan_ltmat33_fill_q()... */
  gan_ltmat33_slmultT_i ( &sm33A ); /* A = A^T*A, macro */
  gan_ltmat33_srmultT_i ( &sm33A ); /* A = A*A^T, macro */

There are also routines to multiply a matrix by the transpose of another matrix of the same size, where the result is assumed to be a symmetric matrix. So mathematically the operations have the form

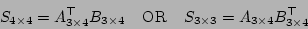
$\begin{displaymath}S_{4\times 4} = A_{3\times 4}^{\top}B_{3\times 4}\;\;\;\;\mbox{OR}\;\;\;\; S_{3\times 3} = A_{3\times 4} B_{3\times 4}^{\top} \end{displaymath}$

The Gandalf macro routines to implement these operations are

  Gan_Matrix34 m34A, m34B;
  Gan_SquMatrix33 sm33S;
  Gan_SquMatrix44 sm44S;

  /* ... set up m34A, m34B using e.g. gan_mat34_fill_q() ... */
  gan_mat34_rmultm34T_sym_q ( &m34A, &m34B, &sm33S ); /* S = A*B^T */
  gan_mat34_lmultm34T_sym_q ( &m34B, &m34A, &sm44S ); /* S = A^T*B */

with equivalent function calls

  sm33S = gan_mat34_rmultm34T_sym_s ( &m34A, &m34B ); /* S = A*B^T */
  sm44S = gan_mat34_lmultm34T_sym_s ( &m34B, &m34A ); /* S = A^T*B */

A common operation is to multiply a symmetric matrix on left and right by a matrix and its transpose, producing another symmetric matrix. Gandalf supports all combinations of these operations. Those involving $3\times 4$ matrices are

  Gan_SquMatrix33 sm33Sa;
  Gan_SquMatrix44 sm44Sb;
  Gan_Matrix34 m34A;

  gan_symmat33_lrmultm34T_q ( &sm33Sa, &m34A, &sm44Sb ); /* Sb = A^T*Sa*A, macro */
  sm44Sb = gan_symmat33_lrmultm34T_s ( &sm33Sa, &m34A ); /* Sb = A^T*Sa*A, function call */
  gan_symmat44_lrmultm34_q ( &sm44Sb, &m34A, &sm33Sa ); /* Sa = A*Sb*A^T, macro */
  sm33Sa = gan_symmat44_lrmultm34_s ( &sm44Sb, &m34A ); /* Sa = A*Sb*A^T, function call */

Error detection: If implicit inverse is used (e.g. the...multl33I_[qsi]() or ...multl33IT_[qsi]() routines), the matrix must be non-singular, which for triangular matrices means that none of the diagonal elements should be zero. If the matrix was produced by successful Cholesky factorisation of a symmetric matrix (see Section 3.1.2.12) the matrix is guaranteed to be non-singular. This is the normal method of creating a triangular matrix, and Gandalf uses assert() to check for the singularity of the matrix.

Next: Fixed size matrix inverse Up: Fixed size matrices Previous: Fixed size matrix/vector multiplication Contents

2006-03-17