General size matrix addition (original) (raw)

Next: General size matrix subtraction Up: General size matrices Previous: Transposing a general size Contents

General size matrix addition

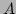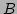To add two matrices $A$ and $B$ together, obtaining the sum 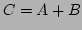$C = A + B$ , use the routine

  Gan_Matrix mA, mB, mC; /* declare matrices A, B and C */

  /* ... create and fill mA & mB, create mC ... */
  gan_mat_add_q ( &mA, &mB, &mC ); /* compute C = A + B */

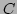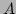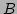Again matrix $C$ is reallocated if necessary. Matrices $A$ and $B$ must of course be the same size, or the error handler is invoked and NULL is returned. The sum matrix 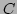$C$ may be create from scratch using

  Gan_Matrix *pmC; /* declare matrix C as pointer */

  /* ... create and fill mA & mB ... */
  pmC = gan_mat_add_s ( &mA, &mB ); /* compute C = A + B */

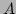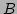Another way of computing matrix addition is to replace one of the input matrix $A$ or $B$ with the result, using one of the in-place routines

  gan_mat_add_i1 ( &mA, &mB ); /* replace A = A + B */
  gan_mat_add_i2 ( &mA, &mB ); /* replace B = A + B */

An alternative to gan_mat_add_i1() is the more explicit routine

  gan_mat_increment ( &mA, &mB ); /* replace A = A + B */

There is also a set of routines for adding a general size matrix to the transpose of another:

  Gan_Matrix mA, mB, mC, *pmC; /* declare matrices A, B and C */

  /* ... create and fill A & B, create C ... */

  /* B must have the same number of columns as A has rows, and vice versa */
  gan_mat_addT_q ( &mA, &mB, &mC ); /* compute C = A + B^T, OR */
  pmC = gan_mat_addT_s ( &mA, &mB ); /* compute C = A + B^T, OR */
  gan_mat_incrementT ( &mA, &mB ); /* replace A = A + B^T */

Another set of routines allows you to add two matrices and generate a symmetric matrix, on the assumption that the result is indeed symmetric. Either matrix may be implicitly transposed for the purpose of the operation:

  Gan_Matrix mA, mB; /* declare matrices A, B */
  Gan_SquMatrix smS, *psmS; /* declare result matrix S */

  /* ... create and fill A & B, create S ... */

  /* for these functions, B must have the same number of columns and rows as A */
  gan_mat_add_sym_q ( &mA, &mB, &smS ); /* S = A + B, OR */
  psmS = gan_mat_add_sym_s ( &mA, &mB ); /* S = A + B */
  gan_matT_addT_sym_q ( &mA, &mB, &smS ); /* S = A^T + B^T, OR */
  psmS = gan_matT_addT_sym_s ( &mA, &mB ); /* S = A^T + B^T */

  /* here B must have the same number of columns as A has rows, and vice versa */
  gan_mat_addT_sym_q ( &mA, &mB, &smS ); /* S = A + B^T, OR */
  psmS = gan_mat_addT_sym_s ( &mA, &mB ); /* S = A + B^T */
  gan_matT_add_sym_q ( &mA, &mB, &smS ); /* S = A^T + B, OR */
  psmS = gan_matT_add_sym_s ( &mA, &mB ); /* S = A^T + B */

Finally we have some routines for adding a matrix to its own transpose, producing a symmetric matrix:

  Gan_Matrix mA; /* declare matrix A */
  Gan_SquMatrix smS, *psmS; /* declare result matrix S */

  /* ... create and fill A, create S ... */

  gan_mat_saddT_sym_q ( &mA, &smS ); /* S = A + A^T, OR */
  psmS = gan_mat_saddT_sym_s ( &mA ); /* S = A + A^T */

There are equivalent functions for square matrices. Firstly the simple routines for adding two matrices:

  Gan_SquMatrix smA, smB, smC, *psmC; /* declare matrices A, B & C */

  /* ... create and fill smA & smB, create smC ... */
  gan_squmat_add_q ( &smA, &smB, &smC ); /* compute C = A + B, OR */
  gan_squmat_add_i1 ( &smA, &smB ); /* replace A = A + B, OR */
  gan_squmat_add_i2 ( &smA, &smB ); /* replace B = A + B, OR */
  gan_squmat_increment ( &smA, &smB ); /* replace A = A + B, OR */
  psmC = gan_squmat_add_s ( &smA, &smB ); /* compute C = A + B as new matrix */

Other routines implicitly transpose one of the input matrices:

  Gan_SquMatrix smA, smB, smC, *psmC; /* declare matrices A, B & C */

  /* ... create and fill smA & smB, create smC ... */
  gan_squmat_addT_q ( &smA, &smB, &smC ); /* compute C = A + B^T, OR */
  gan_squmat_incrementT ( &smA, &smB ); /* replace A = A + B^T, OR */
  psmC = gan_squmat_addT_s ( &smA, &smB ); /* compute C = A + B^T as new matrix */

Error detection: NULL is returned and the Gandalf error handler invoked if the matrix addition fails. The most likely failure modes are failing to create/set the result matrix, or size/type incompatibility between the input matrices.

Next: General size matrix subtraction Up: General size matrices Previous: Transposing a general size Contents

2006-03-17