equalizeLayers - Equalize layer parameters of deep neural network - MATLAB (original) (raw)
Main Content
Equalize layer parameters of deep neural network
Since R2022b
Syntax
Description
Examples
This example shows how to improve the performance of a quantized deep learning model by equalizing layer parameters in the network. Use the equalizeLayers function to adjust the compatible network parameters of compute layers in order to make the layers more suitable for quantization.
The network in this example has a MobileNet-v2 backbone. Transfer learning was used to train the network to classify images in the CIFAR-10 dataset.
Load Pretrained Network and Data
Download the CIFAR-10 data set [1]. The data set contains 60,000 images. Each image is 32-by-32 in size and has three color channels (RGB). The size of the data set is 175 MB. Depending on your internet connection, the download process can take some time.
datadir = tempdir; downloadCIFARData(datadir);
Load the trained network for CIFAR-10 using a MobileNet-v2 backbone. The batch normalization layers have been folded into the convolution and grouped convolution layers.
net = load("CIFARMobilenet.mat").net;
Load the CIFAR-10 training and test images as 4-D arrays. The training set contains 50,000 images and the test set contains 10,000 images. Create an augmentedImageDatastore object to use for network training and validation.
[XTrain,TTrain,XTest,TTest] = loadCIFARData(datadir); inputSize = net.Layers(1).InputSize; augimdsTrain = augmentedImageDatastore(inputSize,XTrain,TTrain); augimdsTest = augmentedImageDatastore(inputSize,XTest,TTest); classes = categories(TTest);
Calculate the accuracy of the trained network on the test data.
scores = minibatchpredict(net,augimdsTest); YTest = scores2label(scores,classes); accuracyOfnet = mean(YTest == TTest)*100; display("Accuracy of original network on validation data: " + accuracyOfnet + "%");
"Accuracy of original network on validation data: 85.92%"You can use the deepNetworkDesigner function to open the Deep Network Designer app and display the network diagram and the total number of learnable parameters in the network.
When you quantize then network to int8 format, it produces an accuracy of 16.8%. This is nearly a 70% degradation compared to the accuracy of the floating-point version of the network.
Analyze Network
One possible cause of major performance degradation during quantization is the significant range variation in the weight tensor of the convolution and grouped convolution layers. To investigate this variation, you can view the layer weights at the filter level for the first depth-wise separable convolution layer.
For a more detailed view, plot the weight tensor as a boxplot across filters.
layerWeights = net.Layers(4).Weights; layerWeights = reshape(layerWeights,[9 32]); boxchart(layerWeights) xlabel("Filters (Groups)") ylabel("Weight Values") title("Weights Ranges of Original Network")
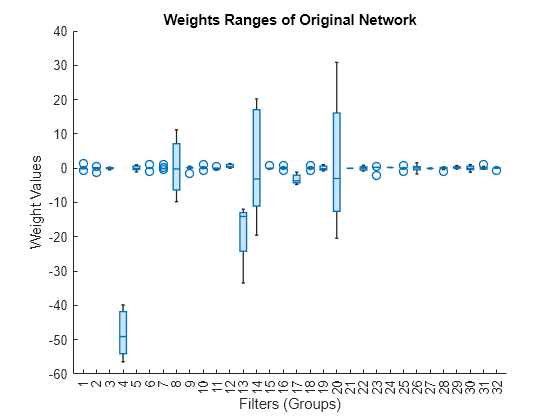
Due to the significant range variation across the filters, many filter groups are not representable after quantization to int8 format. Nonrepresentable filter groups cause severe network degradation when the error produced by nonrepresentable values propagates through the network.
To view the histogram bins across different layers, import a calibrated dlquantizer object into the Deep Network Quantizer app. The app displays histograms of the dynamic ranges of the parameters as well as the minimum and maximum values across each network layer parameter tensor. Quantization of Deep Neural Networks explains this process in detail.
Use equalizeLayers to Adjust Network Parameters
You can use the equalizeLayers function to improve the network quantization behavior. The equalizeLayers function can be used on networks that have linear activation functions that exhibit a positive scale equivariance property [1]. The equalizeLayers function tries to find compatible layers and modifies the weights to make the network more suitable for quantization. The function modifies the layer weights in such a way that the overall numerical output of the network is unchanged.
Equalize the layers in the network.
equalizedNet = equalizeLayers(net);
Quantize Equalized Network
After you equalize the layers, quantize the network. Compare the accuracy of the quantized network with and without equalized layers.
Create a dlquantizer object for the equalized network.
dlQuantObj = dlquantizer(equalizedNet);
Define calibration data to use for quantization.
numberOfCalibrationImages = 500; augimdsCalibration = subset(augimdsTrain,1:numberOfCalibrationImages);
Calibrate the dlquantizer object.
calibStats = calibrate(dlQuantObj,augimdsCalibration)
calibStats=159×5 table Optimized Layer Name Network Layer Name Learnables / Activations MinValue MaxValue _________________________________ ___________________________ ________________________ ________ ________
"imageinput_Mean" {'imageinput' } "Mean" 99.412 109.91
"imageinput_StandardDeviation" {'imageinput' } "StandardDeviation" 67.506 69.615
"Conv1_Weights" {'Conv1' } "Weights" -1.9843 1.5405
"Conv1_Bias" {'Conv1' } "Bias" -5.8864 4.7606
"expanded_conv_depthwise_Weights" {'expanded_conv_depthwise'} "Weights" -2.1183 1.5631
"expanded_conv_depthwise_Bias" {'expanded_conv_depthwise'} "Bias" -2.3202 4.1318
"expanded_conv_project_Weights" {'expanded_conv_project' } "Weights" -2.1404 1.9959
"expanded_conv_project_Bias" {'expanded_conv_project' } "Bias" -9.1792 10.327
"block_1_expand_Weights" {'block_1_expand' } "Weights" -0.85797 1.1262
"block_1_expand_Bias" {'block_1_expand' } "Bias" -2.2402 4.8886
"block_1_depthwise_Weights" {'block_1_depthwise' } "Weights" -1.5857 2.3307
"block_1_depthwise_Bias" {'block_1_depthwise' } "Bias" -8.9999 9.0277
"block_1_project_Weights" {'block_1_project' } "Weights" -3.9702 2.3751
"block_1_project_Bias" {'block_1_project' } "Bias" -15.641 17.965
"block_2_expand_Weights" {'block_2_expand' } "Weights" -0.41095 0.36931
"block_2_expand_Bias" {'block_2_expand' } "Bias" -2.1926 4.034
⋮Use the quantize function to create a simulatable quantized network from the dlquantizer object.
qNetEqualized = quantize(dlQuantObj);
Evaluate the accuracy of the quantized network. The table compares the accuracy of the original floating-point network, the quantized network without equalized layers, and the quantized network with equalized layers.
qscores = minibatchpredict(qNetEqualized,augimdsTest); YTest = scores2label(qscores,classes); accuracyOfQuantizedNet = mean(YTest == TTest)*100; createComparisonTable(accuracyOfnet,accuracyOfQuantizedNet)
ans=1×3 table Original Network Quantized Original Network Quantized Equalized Network ________________ __________________________ ___________________________
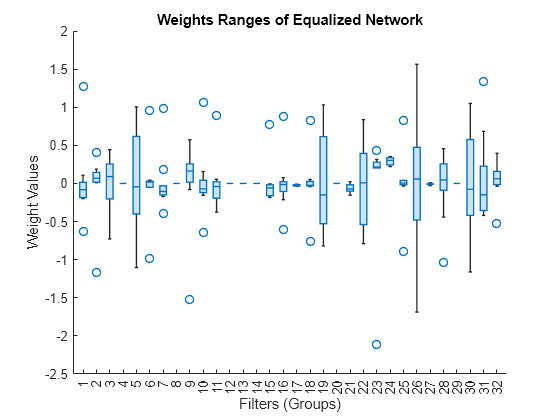
Test Data Accuracy (%) 85.92 16.81 76.63 Plot the new weight tensor as a boxplot across the filters. The weight ranges for the equalized network are better distributed and the quantized equalized network performance is significantly better than the quantized network without layer equalization.
newLayerWeights = equalizedNet.Layers(4).Weights; newLayerWeights = reshape(newLayerWeights,[9 32]); boxchart(newLayerWeights) xlabel("Filters (Groups)") ylabel("Weight Values") title("Weights Ranges of Equalized Network")
**Helper Functions
The createComparisonTable helper function prints a table comparing the accuracy of the original floating-point network, the quantized network without equalized layers, and the quantized network with equalized layers.
function comparisonTable = createComparisonTable(originalAccuracy,accuracyQuantizedEqualizedNet) % Create the summary table comparisonTable = table(originalAccuracy,16.81,accuracyQuantizedEqualizedNet, ... VariableNames=["Original Network", "Quantized Original Network", "Quantized Equalized Network"], ... RowNames="Test Data Accuracy (%)"); end
Input Arguments
Output Arguments
Equalized network, returned as a DAGNetwork,SeriesNetwork, dlnetwork,yolov2ObjectDetector, or ssdObjectDetector object. The type of network that the function returns is the same as thenet input.
References
[1] Nagel, Markus, Mart Van Baalen, Tijmen Blankevoort, and Max Welling. "Data-Free Quantization Through Weight Equalization and Bias Correction." In 2019 IEEE/CVF International Conference on Computer Vision (ICCV), 1325-34. Seoul, Korea (South): IEEE, 2019. https://doi.ogg/10.1109/ICCV.2019.00141.
Version History
Introduced in R2022b