Similarity Transformation and Matrix Diagonalization (original) (raw)
A square matrix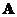 
is similar to a square matrix
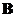if there is a non-singular matrix such that
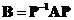. Let us call matrix
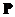as a modal matrix.
Similarity transformation has several properties:
Since diagonal matrix has many nice properties similar to a scalar, we would like to find matrix similarity to a diagonal matrix. The only requirement to perform similarity transformation is to find a non singular modal matrix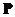
such that
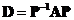. We can form modal matrix
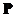from the eigenvector of matrix
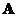. However, we are not sure if the modal matrix
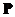is nonsingular (has inverse).
We know that modal matrix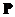
is nonsingular when the eigenvectors of the square matrix
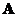are being linearly independent . But, again we are not sure whether the eigenvectors of the square matrix
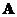will be linearly independent. We only know that if all the eigenvalues of the square matrix
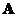are distinct (do not have any eigenvalue of multiple values) then the eigenvectors are linearly independent. Thus, any square matrix with distinct eigenvalues can be converted into diagonal matrix by similarity transformation
.
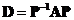To obtain modal matrix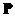
, we perform horizontal concatenation of the
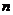linearly independent eigenvectors of matrix
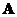such that
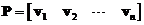. Since eigenvalues of matrix
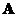are all distinct, modal matrix
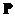has full rank because the eigenvectors are linearly independent, therefore modal matrix
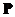has inverse (nonsingular). The diagonal elements of diagonal matrix
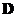consist of the eigenvalues of
.
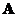Example:
Example:
Matrix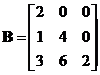
has eigenvalues
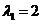(with algebraic multiplicity of 2) and
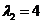(simple). The first eigenvalue
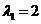has corresponding eigenvector
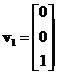and
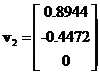. The first eigenvalue
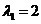has geometric multiplicity of 2 because the two eigenvectors
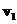and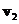
are linearly independent. The second eigenvalue
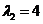has corresponding eigenvector
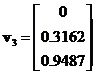. Since matrix
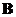has 3 linearly independent eigenvectors, matrix
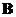is non-defective. We can form modal matrix
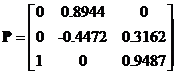such that
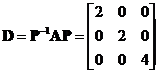. Notice in this example that the eigenvalues are not all distinct but the eigenvectors are linearly independent, therefore the matrix is diagonalizable.
Example:
Matrix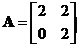
has multiple eigenvalue of
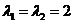. The eigenvectors associated with eigenvalues are vectors of the form of
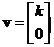for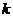
any non-zero real number. Since the eigenvectors are linearly dependent, the modal matrix
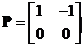has no inverse and therefore matrix
is non-diagonalizable.
See also : Matrix Eigen Value & Eigen Vector , Matrix Power , Equal matrix
Rate this tutorial or give your comments about this tutorial