Linear Algebra tutorial Solving System Linear Equations (original) (raw)
Solving System Linear Equation
Linear equation is an equation in the form of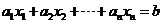 
The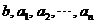 
are the known constant.
The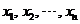 
are the 
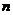unknown variables. The problem in linear equation is to find the values of the unknown variables that satisfy the equation.
For example, when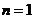
, 
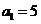and 
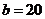we have linear equation 
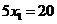and the solution is
.
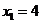We may also have several equations and several unknowns that we would like to find out. A linear system is a set of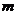 
linear equations each in 
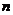unknown. We can write a linear system as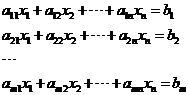
When we have many equations and many unknowns, it is easier to represent the linear system into matrix. We put the constant coefficients of the equations into a matrix, and then we can multiply with the unknown to obtain the constants. To transform the system of linear equations into matrix format, you need to reorder the equations according to the order of the unknowns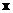 
and put the coefficients of the unknowns into matrix coefficients
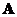. The constants on the right hand side of the equation are written into vector constants
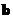. The linear system above can be written as
Thus, a linear system can be simplified into a matrix product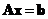
A solution of the linear system is an ordered collection of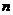 
numbers that satisfies the 
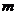linear equations, which can be written in short as a vector solution
.
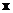Example:
Solve a linear system with three equations and three unknowns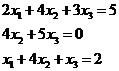
The linear system can be written as 
where matrix
and 
The solution of the linear system is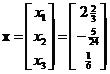
The interactive program below will help you to solve a system of linear equations
. To use the program, first you need to transform your system of linear equations into matrix format as explained in the example above. Your input is matrix coefficients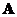 
and vector constants
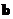. Then you click “Solve Linear System Ax=b” button and the program will produce the vector solution
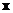. Optionally, you can select your output is either in decimal or in rational format. The rational output is an approximation of the decimal format. When you click “Random Example” button, it will create random input matrix to provide you with more examples of linear system. Note that if the coefficient matrix is singular or nearly singular, you will get only the approximate solution in least square sense using generalized inverse such that the error is minimized 
.
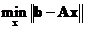Notes
Some important notes on linear systems are:
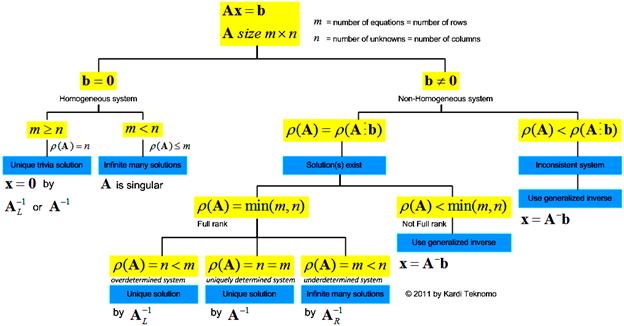
See also: Generalized Inverse, matrix rank, determinant, Solving Linear equations using MS Excel
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\