Polynomial interpolation — scikit-learn 0.20.4 documentation (original) (raw)
Note
Click here to download the full example code
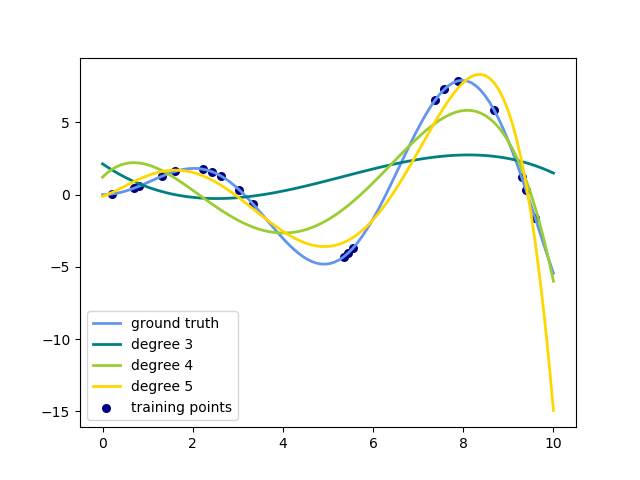
This example demonstrates how to approximate a function with a polynomial of degree n_degree by using ridge regression. Concretely, from n_samples 1d points, it suffices to build the Vandermonde matrix, which is n_samples x n_degree+1 and has the following form:
[[1, x_1, x_1 ** 2, x_1 ** 3, …],
[1, x_2, x_2 ** 2, x_2 ** 3, …], …]
Intuitively, this matrix can be interpreted as a matrix of pseudo features (the points raised to some power). The matrix is akin to (but different from) the matrix induced by a polynomial kernel.
This example shows that you can do non-linear regression with a linear model, using a pipeline to add non-linear features. Kernel methods extend this idea and can induce very high (even infinite) dimensional feature spaces.
Out:
print(doc)
Author: Mathieu Blondel
Jake Vanderplas
License: BSD 3 clause
import numpy as np import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline
def f(x): """ function to approximate by polynomial interpolation""" return x * np.sin(x)
generate points used to plot
x_plot = np.linspace(0, 10, 100)
generate points and keep a subset of them
x = np.linspace(0, 10, 100) rng = np.random.RandomState(0) rng.shuffle(x) x = np.sort(x[:20]) y = f(x)
create matrix versions of these arrays
X = x[:, np.newaxis] X_plot = x_plot[:, np.newaxis]
colors = ['teal', 'yellowgreen', 'gold'] lw = 2 plt.plot(x_plot, f(x_plot), color='cornflowerblue', linewidth=lw, label="ground truth") plt.scatter(x, y, color='navy', s=30, marker='o', label="training points")
for count, degree in enumerate([3, 4, 5]): model = make_pipeline(PolynomialFeatures(degree), Ridge()) model.fit(X, y) y_plot = model.predict(X_plot) plt.plot(x_plot, y_plot, color=colors[count], linewidth=lw, label="degree %d" % degree)
plt.legend(loc='lower left')
plt.show()
Total running time of the script: ( 0 minutes 0.163 seconds)