Accelerate MATLAB Algorithm by Generating MEX Function - MATLAB & Simulink (original) (raw)

You can use MATLAB® Coder™ to generate a MEX function from your MATLAB code. A MEX function is a MATLAB executable. It is generated code that can be called from inside MATLAB. While working inside the MATLAB environment, use MEX functions to accelerate the computationally intensive portions of your MATLAB code. Generate a MEX function from your MATLAB code by using the MATLAB Coder app or by using codegen at the MATLAB command line.

In this tutorial, you use the MATLAB Coder codegen command to generate a MEX function for a MATLAB function. You first generate a MEX function that can accept only inputs that have fixed, preassigned size. You then generate another MEX function that can accept inputs of many different sizes.

MATLAB Coder generates code from MATLAB functions, not scripts. If your MATLAB code is in the form of a script, create a wrapper function around the script before generating code.

Tutorial Files: Euclidean Distance

Open this example to obtain the files for this tutorial.

Description of Tutorial Files

This tutorial uses the euclidean_data.mat,euclidean.m, euclidean_test.m,euclidean_test_2d.m, build_mex_fixed.m, and build_mex_variable.m files.

• The MATLAB data file euclidean_data.mat contains two pieces of data: a single point in three-dimensional Euclidean space and a set of several other points in three-dimensional Euclidean space. More specifically:
  • x is a3-by-1 column vector that represents a point in three-dimensional Euclidean space.
  • cb is a3-by-216 array. Each column in cb represents a point in three-dimensional Euclidean space.
• The MATLAB file euclidean.m contains the functioneuclidean that implements the core algorithm in this example. The function takesx and cb as inputs. It calculates the Euclidean distance between x and each point in cb and returns these quantities:
  • The column vector y_min, which is equal to the column in cb that represents the point closest to x.
  • The column vector y_max, which is equal to the column in cb that represents the point farthest from x.
  • The 2-dimensional vector idx that contains the column indices of the vectorsy_min and y_max incb.
  • The 2-dimensional vector distance that contains the calculated smallest and largest distances tox.
    function [y_min,y_max,idx,distance] = euclidean(x,cb)
    % Initialize minimum distance as distance to first element of cb
    % Initialize maximum distance as distance to first element of cb
    idx(1)=1;
    idx(2)=1;
    distance(1)=norm(x-cb(:,1));
    distance(2)=norm(x-cb(:,1));
    % Find the vector in cb with minimum distance to x
    % Find the vector in cb with maximum distance to x
    for index=2:size(cb,2)
    d=norm(x-cb(:,index));
    if d < distance(1)
    distance(1)=d;
    idx(1)=index;
    end
    if d > distance(2)
    distance(2)=d;
    idx(2)=index;
    end
    end
    % Output the minimum and maximum distance vectors
    y_min=cb(:,idx(1));
    y_max=cb(:,idx(2));
    end
• The MATLAB script euclidean_test.m loads the data file euclidean_data.mat into the workspace. It calls the function euclidean to calculatey_min, y_max,idx, and distance. The script then displays the calculated quantities at the command line.
  Loading euclidean_data.mat is the preprocessing step that is executed before calling the core algorithm. Displaying the results is the post-processing step.
  % Load test data
  load euclidean_data.mat
  % Determine closest and farthest points and corresponding distances
  [y_min,y_max,idx,distance] = euclidean(x,cb);
  % Display output for the closest point
  disp('Coordinates of the closest point are: ');
  disp(num2str(y_min'));
  disp(['Index of the closest point is ', num2str(idx(1))]);
  disp(['Distance to the closest point is ', num2str(distance(1))]);
  disp(newline);
  % Display output for the farthest point
  disp('Coordinates of the farthest point are: ');
  disp(num2str(y_max'));
  disp(['Index of the farthest point is ', num2str(idx(2))]);
  disp(['Distance to the farthest point is ', num2str(distance(2))]);
• The MATLAB script euclidean_test_2d.m is a modification of euclidean_test.m for points in two-dimensional Euclidean space. The contents ofeuclidean_test_2d.m are shown later in the tutorial, when you use it to test the MEX function for variable-size inputs.
• The build scripts build_mex_fixed.m andbuild_mex_variable.m contain commands for generating MEX functions from your MATLAB code that accept fixed-size and variable-size inputs, respectively. The contents of these scripts are shown later in the tutorial, when you generate the C code.

Tip

Use test scripts to separate the pre- and post-processing steps from the function that implements the core algorithm. This practice enables you to easily reuse your algorithm. You generate code for the MATLAB function implementing the core algorithm. You do not generate code for the test script.

Generate MEX Function for the MATLAB Function

Run the Original MATLAB Code

Run the test script euclidean_test.m in MATLAB. The output displays y, idx, and distance.

Coordinates of the closest point are: 0.8 0.8 0.4 Index of the closest point is 171 Distance to the closest point is 0.080374

Coordinates of the farthest point are: 0 0 1 Index of the farthest point is 6 Distance to the farthest point is 1.2923

Make the MATLAB Code Suitable for Code Generation

To make your MATLAB code suitable for code generation, you use the Code Analyzer and the Code Generation Readiness Tool. The Code Analyzer in the MATLAB Editor continuously checks your code as you enter it. It reports issues and recommends modifications to maximize performance and maintainability. The Code Generation Readiness Tool screens the MATLAB code for features and functions that are not supported for code generation.

Certain MATLAB built-in functions and toolbox functions, classes, and System objects that are supported for C/C++ code generation have specific code generation limitations. These limitations and related usage notes are listed in the Extended Capabilities sections of their corresponding reference pages. For more information, see Functions and Objects Supported for C/C++ Code Generation.

1. Open euclidean.m in the MATLAB Editor. The Code Analyzer message indicator in the top right corner of the MATLAB Editor is green. The analyzer did not detect errors, warnings, or opportunities for improvement in the code.
2. After the function declaration, add the %#codegen directive:
   function [y,idx,distance] = euclidean(x,cb) %#codegen
   The%#codegen directive prompts the Code Analyzer to identify warnings and errors specific to code generation.
   The Code Analyzer message indicator becomes red, indicating that it has detected code generation issues.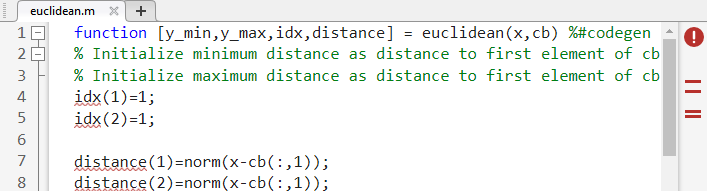
   
3. To view the warning messages, move your cursor to the underlined code fragments. The warnings indicate that code generation requires the variables idx and distance to be fully defined before subscripting them. This warning appears because the code generator determines the sizes of variables at their first appearance in the code. To fix this issue, use the ones function to simultaneously allocate and initialize these arrays.
   % Initialize minimum distance as distance to first element of cb
   % Initialize maximum distance as distance to first element of cb
   idx = ones(1,2);
   distance = ones(1,2)*norm(x-cb(:,1));
   The Code Analyzer message indicator becomes green again, indicating that it does not detect any more code generation issues.
   
   For more information about using the Code Analyzer, see Check Code for Errors and Warnings Using the Code Analyzer.
4. Save the file.
5. To run the Code Generation Readiness Tool, call thecoder.screener function from the MATLAB command line:
   coder.screener('euclidean')
   The tool does not detect any code generation issues for euclidean. For more information, see Code Generation Readiness Tool.
   Note
   The Code Analyzer and the Code Generation Readiness Tool might not detect all code generation issues. After eliminating the errors or warnings that these tools detect, generate code by using MATLAB Coder to determine if your MATLAB code has other compliance issues.

You are now ready to compile your code by using the codegen command. Here,compilation refers to the generation of C/C++ code from your MATLAB code.

Note

Compilation of MATLAB code refers to the generation of C/C++ code from the MATLAB code. In other contexts, the term compilation could refer to the action of a C/C++ compiler.

Defining Input Types

Because C uses static typing, the code generator must determine the class, size, and complexity of all variables in the MATLAB files at code generation time, also known as compile time. Therefore, when you generate code for the files, you must specify the properties of all input arguments to the entry-point functions. An entry-point function is a top-level MATLAB function from which you generate code.

When you generate code by using the codegen command, use the -args option to specify sample input parameters to the entry-point functions. The code generator uses this information to determine the properties of the input arguments.

In the next step, you use the codegen command to generate a MEX file from your entry-point function euclidean.

Generate and Validate the MEX Function

The build script build_mex_fixed.m contains the commands that you use to generate and validate a MEX function foreuclidean.m. To validate the MEX function, you run the test script euclidean_test with calls to the MATLAB function euclidean replaced with calls to the generated MEX function.

% Load the test data load euclidean_data.mat % Generate code for euclidean.m with codegen. Use the test data as example input. % Validate MEX by using euclidean_test.m. codegen -report euclidean.m -args {x, cb} -test euclidean_test

Note that:

• By default, codegen generates a MEX function named euclidean_mex in the current folder.
• The -report option instructscodegen to generate a code generation report that you can use to debug code generation issues and verify that your MATLAB code is suitable for code generation.
• The -args option specifies sample input parameters to the entry-point function euclidean. The code generator uses this information to determine the class, size, and complexity of the input arguments.
• You use the -test option to run the test fileeuclidean_test.m. This option replaces the calls to euclidean in the test file with calls toeuclidean_mex.

For more information on the code generation options, see codegen.

1. Run the build script build_mex_fixed.m.
   The code generator produces a MEX functioneuclidean_mex in the current working folder.
   The output is:
   Code generation successful: View report.
   Running test file: 'euclidean_test' with MEX function 'euclidean_mex'.
   Coordinates of the closest point are:
   0.8 0.8 0.4

Index of the closest point is 171
Distance to the closest point is 0.080374
Coordinates of the farthest point are:
0 0 1
Index of the farthest point is 6
Distance to the farthest point is 1.2923
This output matches the output that was generated by the original MATLAB function and verifies the MEX function. 2. To view the code generation report in the Report Viewer, clickView report.
If the code generator detects errors or warnings during code generation, the report describes the issues and provides links to the problematic MATLAB code. See Code Generation Reports.

Tip

Use a build script to generate code at the command line. A build script automates a series of MATLAB commands that you perform repeatedly at the command line, saving you time and eliminating input errors.

Generate MEX Function for Variable-Size Inputs

The MEX function that you generated for euclidean.m can accept only inputs that have the same size as the sample inputs that you specified during code generation. However, the input arrays to the corresponding MATLAB function can be of any size. In this part of the tutorial, you generate a MEX function fromeuclidean.m that accepts variable-size inputs.

Suppose that you want the dimensions of x andcb in the generated MEX function to have these properties:

• The first dimension of both x andcb can vary in size up to3.
• The second dimension of x is fixed and has the value 1.
• The second dimension of cb can vary in size up to216.

To specify these input properties, you use the coder.typeof function. coder.typeof(A,B,1) specifies a variable-size input with the same class and complexity asA and upper bounds given by the corresponding element of the size vector B. Use the build scriptbuild_mex_variable.m that usescoder.typeof to specify the properties of variable-size inputs in the generated MEX function.

% Load the test data load euclidean_data.mat

% Use coder.typeof to specify variable-size inputs eg_x=coder.typeof(x,[3 1],1); eg_cb=coder.typeof(cb,[3 216],1);

% Generate code for euclidean.m using coder.typeof to specify % upper bounds for the example inputs codegen -report euclidean.m -args {eg_x,eg_cb}

You can verify that the new MEX function euclidean_mex accepts inputs of dimensions different from those of x andcb. The test script euclidean_test_2d.m creates the input arrays x2d and cb2d that are two-dimensional versions of x and cb, respectively. It then calls the MATLAB function euclidean by using these input parameters.

% Load the test data load euclidean_data.mat

% Create 2-D versions of x and cb x2d=x(1:2,:); cb2d=cb(1:2,1:6:216);

% Determine closest and farthest points and corresponding distances [y_min,y_max,idx,distance] = euclidean(x2d,cb2d);

% Display output for the closest point disp('Coordinates of the closest point are: '); disp(num2str(y_min')); disp(['Index of the closest point is ', num2str(idx(1))]); disp(['Distance to the closest point is ', num2str(distance(1))]);

disp(newline);

% Display output for the farthest point disp('Coordinates of the farthest point are: '); disp(num2str(y_max')); disp(['Index of the farthest point is ', num2str(idx(2))]); disp(['Distance to the farthest point is ', num2str(distance(2))]);

Running euclidean_test_2d.m produces the output:

Coordinates of the closest point are: 0.8 0.8 Index of the closest point is 29 Distance to the closest point is 0.078672

Coordinates of the farthest point are: 0 0 Index of the farthest point is 1 Distance to the farthest point is 1.1357

To run the test script euclidean_test_2d.m with the calls toeuclidean replaced with calls toeuclidean_mex, use coder.runTest.

coder.runTest('euclidean_test_2d','euclidean')

The output matches the output generated by the original MATLAB function. This verifies the fact that the new MEX function can accept inputs of dimensions different from those of x andcb.

See Also

codegen | coder.screener | coder.runTest

Topics

• Functions and Objects Supported for C/C++ Code Generation
• C++ Code Generation
• Create and Edit Input Types by Using the Coder Type Editor
• Optimize Generated C/C++ and MEX Code
• Code Generation Reports
• Profile MEX Functions by Using MATLAB Profiler