Least squares (original) (raw)

Approximation method in statistics

The result of fitting a set of data points with a quadratic function

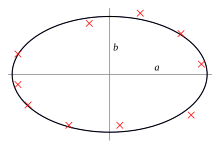
Conic fitting a set of points using least-squares approximation

The method of least squares is a parameter estimation method in regression analysis based on minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. (More simply, least squares is a mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve.)

The most important application is in data fitting. When the problem has substantial uncertainties in the independent variable (the x variable), then simple regression and least-squares methods have problems; in such cases, the methodology required for fitting errors-in-variables models may be considered instead of that for least squares.

Least squares problems fall into two categories: linear or ordinary least squares and nonlinear least squares, depending on whether or not the model functions are linear in all unknowns. The linear least-squares problem occurs in statistical regression analysis; it has a closed-form solution. The nonlinear problem is usually solved by iterative refinement; at each iteration the system is approximated by a linear one, and thus the core calculation is similar in both cases.

Polynomial least squares describes the variance in a prediction of the dependent variable as a function of the independent variable and the deviations from the fitted curve.

When the observations come from an exponential family with identity as its natural sufficient statistics and mild-conditions are satisfied (e.g. for normal, exponential, Poisson and binomial distributions), standardized least-squares estimates and maximum-likelihood estimates are identical.[1] The method of least squares can also be derived as a method of moments estimator.

The following discussion is mostly presented in terms of linear functions but the use of least squares is valid and practical for more general families of functions. Also, by iteratively applying local quadratic approximation to the likelihood (through the Fisher information), the least-squares method may be used to fit a generalized linear model.

The least-squares method was officially discovered and published by Adrien-Marie Legendre (1805),[2] though it is usually also co-credited to Carl Friedrich Gauss (1809),[3][4] who contributed significant theoretical advances to the method,[4] and may have also used it in his earlier work in 1794 and 1795.[5][4]

The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on land sightings for navigation.

The method was the culmination of several advances that took place during the course of the eighteenth century:[6]

Carl Friedrich Gauss

The first clear and concise exposition of the method of least squares was published by Legendre in 1805.[7] The technique is described as an algebraic procedure for fitting linear equations to data and Legendre demonstrates the new method by analyzing the same data as Laplace for the shape of the Earth. Within ten years after Legendre's publication, the method of least squares had been adopted as a standard tool in astronomy and geodesy in France, Italy, and Prussia, which constitutes an extraordinarily rapid acceptance of a scientific technique.[6]

In 1809 Carl Friedrich Gauss published his method of calculating the orbits of celestial bodies. In that work he claimed to have been in possession of the method of least squares since 1795.[8] This naturally led to a priority dispute with Legendre. However, to Gauss's credit, he went beyond Legendre and succeeded in connecting the method of least squares with the principles of probability and to the normal distribution. He had managed to complete Laplace's program of specifying a mathematical form of the probability density for the observations, depending on a finite number of unknown parameters, and define a method of estimation that minimizes the error of estimation. Gauss showed that the arithmetic mean is indeed the best estimate of the location parameter by changing both the probability density and the method of estimation. He then turned the problem around by asking what form the density should have and what method of estimation should be used to get the arithmetic mean as estimate of the location parameter. In this attempt, he invented the normal distribution.

An early demonstration of the strength of Gauss's method came when it was used to predict the future location of the newly discovered asteroid Ceres. On 1 January 1801, the Italian astronomer Giuseppe Piazzi discovered Ceres and was able to track its path for 40 days before it was lost in the glare of the Sun. Based on these data, astronomers desired to determine the location of Ceres after it emerged from behind the Sun without solving Kepler's complicated nonlinear equations of planetary motion. The only predictions that successfully allowed Hungarian astronomer Franz Xaver von Zach to relocate Ceres were those performed by the 24-year-old Gauss using least-squares analysis.

In 1810, after reading Gauss's work, Laplace, after proving the central limit theorem, used it to give a large sample justification for the method of least squares and the normal distribution. In 1822, Gauss was able to state that the least-squares approach to regression analysis is optimal in the sense that in a linear model where the errors have a mean of zero, are uncorrelated, normally distributed, and have equal variances, the best linear unbiased estimator of the coefficients is the least-squares estimator. An extended version of this result is known as the Gauss–Markov theorem.

The idea of least-squares analysis was also independently formulated by the American Robert Adrain in 1808. In the next two centuries workers in the theory of errors and in statistics found many different ways of implementing least squares.[9]

The objective consists of adjusting the parameters of a model function to best fit a data set. A simple data set consists of n points (data pairs) ( x i , y i ) {\displaystyle (x_{i},y_{i})\!} {\displaystyle (x_{i},y_{i})\!}, i = 1, …, n, where x i {\displaystyle x_{i}\!} {\displaystyle x_{i}\!} is an independent variable and y i {\displaystyle y_{i}\!} {\displaystyle y_{i}\!} is a dependent variable whose value is found by observation. The model function has the form f ( x , β ) {\displaystyle f(x,{\boldsymbol {\beta }})} {\displaystyle f(x,{\boldsymbol {\beta }})}, where m adjustable parameters are held in the vector β {\displaystyle {\boldsymbol {\beta }}} {\displaystyle {\boldsymbol {\beta }}}. The goal is to find the parameter values for the model that "best" fits the data. The fit of a model to a data point is measured by its residual, defined as the difference between the observed value of the dependent variable and the value predicted by the model: r i = y i − f ( x i , β ) . {\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }}).} {\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }}).}

The residuals are plotted against corresponding x {\displaystyle x} {\displaystyle x} values. The random fluctuations about r i = 0 {\displaystyle r_{i}=0} {\displaystyle r_{i}=0} indicate a linear model is appropriate.

The least-squares method finds the optimal parameter values by minimizing the sum of squared residuals, S {\displaystyle S} {\displaystyle S}:[10] S = ∑ i = 1 n r i 2 . {\displaystyle S=\sum _{i=1}^{n}r_{i}^{2}.} {\displaystyle S=\sum _{i=1}^{n}r_{i}^{2}.}

In the simplest case f ( x i , β ) = β {\displaystyle f(x_{i},{\boldsymbol {\beta }})=\beta } {\displaystyle f(x_{i},{\boldsymbol {\beta }})=\beta } and the result of the least-squares method is the arithmetic mean of the input data.

An example of a model in two dimensions is that of the straight line. Denoting the y-intercept as β 0 {\displaystyle \beta _{0}} {\displaystyle \beta _{0}} and the slope as β 1 {\displaystyle \beta _{1}} {\displaystyle \beta _{1}}, the model function is given by f ( x , β ) = β 0 + β 1 x {\displaystyle f(x,{\boldsymbol {\beta }})=\beta _{0}+\beta _{1}x} {\displaystyle f(x,{\boldsymbol {\beta }})=\beta _{0}+\beta _{1}x}. See linear least squares for a fully worked out example of this model.

A data point may consist of more than one independent variable. For example, when fitting a plane to a set of height measurements, the plane is a function of two independent variables, x and z, say. In the most general case there may be one or more independent variables and one or more dependent variables at each data point.

To the right is a residual plot illustrating random fluctuations about r i = 0 {\displaystyle r_{i}=0} {\displaystyle r_{i}=0}, indicating that a linear model ( Y i = β 0 + β 1 x i + U i ) {\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+U_{i})} {\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+U_{i})} is appropriate. U i {\displaystyle U_{i}} {\displaystyle U_{i}} is an independent, random variable.[10]

The residuals are plotted against the corresponding x {\displaystyle x} {\displaystyle x} values. The parabolic shape of the fluctuations about r i = 0 {\displaystyle r_{i}=0} {\displaystyle r_{i}=0} indicates a parabolic model is appropriate.

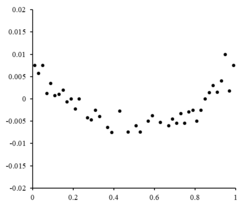
If the residual points had some sort of a shape and were not randomly fluctuating, a linear model would not be appropriate. For example, if the residual plot had a parabolic shape as seen to the right, a parabolic model ( Y i = β 0 + β 1 x i + β 2 x i 2 + U i ) {\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+\beta _{2}x_{i}^{2}+U_{i})} {\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+\beta _{2}x_{i}^{2}+U_{i})} would be appropriate for the data. The residuals for a parabolic model can be calculated via r i = y i − β ^ 0 − β ^ 1 x i − β ^ 2 x i 2 {\displaystyle r_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i}-{\hat {\beta }}_{2}x_{i}^{2}} {\displaystyle r_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i}-{\hat {\beta }}_{2}x_{i}^{2}}.[10]

This regression formulation considers only observational errors in the dependent variable (but the alternative total least squares regression can account for errors in both variables). There are two rather different contexts with different implications:

Solving the least squares problem

[edit]

The minimum of the sum of squares is found by setting the gradient to zero. Since the model contains m parameters, there are m gradient equations: ∂ S ∂ β j = 2 ∑ i r i ∂ r i ∂ β j = 0 , j = 1 , … , m , {\displaystyle {\frac {\partial S}{\partial \beta _{j}}}=2\sum _{i}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,} {\displaystyle {\frac {\partial S}{\partial \beta _{j}}}=2\sum _{i}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}and since r i = y i − f ( x i , β ) {\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }})} {\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }})}, the gradient equations become − 2 ∑ i r i ∂ f ( x i , β ) ∂ β j = 0 , j = 1 , … , m . {\displaystyle -2\sum _{i}r_{i}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m.} {\displaystyle -2\sum _{i}r_{i}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m.}

The gradient equations apply to all least squares problems. Each particular problem requires particular expressions for the model and its partial derivatives.[12]

Linear least squares

[edit]

A regression model is a linear one when the model comprises a linear combination of the parameters, i.e., f ( x , β ) = ∑ j = 1 m β j ϕ j ( x ) , {\displaystyle f(x,{\boldsymbol {\beta }})=\sum _{j=1}^{m}\beta _{j}\phi _{j}(x),} {\displaystyle f(x,{\boldsymbol {\beta }})=\sum _{j=1}^{m}\beta _{j}\phi _{j}(x),}where the function ϕ j {\displaystyle \phi _{j}} {\displaystyle \phi _{j}} is a function of x {\displaystyle x} {\displaystyle x}.[12]

Letting X i j = ϕ j ( x i ) {\displaystyle X_{ij}=\phi _{j}(x_{i})} {\displaystyle X_{ij}=\phi _{j}(x_{i})} and putting the independent and dependent variables in matrices X {\displaystyle X} {\displaystyle X} and Y {\displaystyle Y} {\displaystyle Y}, respectively, we can compute the least squares in the following way. Note that D {\displaystyle D} {\displaystyle D} is the set of all data.[12][13] L ( D , β ) = ‖ Y − X β ‖ 2 = ( Y − X β ) T ( Y − X β ) = Y T Y − Y T X β − β T X T Y + β T X T X β {\displaystyle L(D,{\boldsymbol {\beta }})=\left\|Y-X{\boldsymbol {\beta }}\right\|^{2}=(Y-X{\boldsymbol {\beta }})^{\mathsf {T}}(Y-X{\boldsymbol {\beta }})=Y^{\mathsf {T}}Y-Y^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}} {\displaystyle L(D,{\boldsymbol {\beta }})=\left\|Y-X{\boldsymbol {\beta }}\right\|^{2}=(Y-X{\boldsymbol {\beta }})^{\mathsf {T}}(Y-X{\boldsymbol {\beta }})=Y^{\mathsf {T}}Y-Y^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}} = Y T Y − X T Y β − X T Y β + X T X β 2 {\displaystyle =Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}} {\displaystyle =Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}}

The gradient of the loss is: ∂ L ( D , β ) ∂ β = ∂ ( Y T Y − X T Y β − X T Y β + X T X β 2 ) ∂ β = − 2 X T Y + 2 X T X β {\displaystyle {\frac {\partial L(D,{\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\frac {\partial \left(Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}\right)}{\partial {\boldsymbol {\beta }}}}=-2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}} {\displaystyle {\frac {\partial L(D,{\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\frac {\partial \left(Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}\right)}{\partial {\boldsymbol {\beta }}}}=-2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}}

Setting the gradient of the loss to zero and solving for β {\displaystyle {\boldsymbol {\beta }}} {\displaystyle {\boldsymbol {\beta }}}, we get:[13][12] − 2 X T Y + 2 X T X β = 0 ⇒ X T Y = X T X β {\displaystyle -2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}=0\Rightarrow X^{\mathsf {T}}Y=X^{\mathsf {T}}X{\boldsymbol {\beta }}} {\displaystyle -2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}=0\Rightarrow X^{\mathsf {T}}Y=X^{\mathsf {T}}X{\boldsymbol {\beta }}} β ^ = ( X T X ) − 1 X T Y {\displaystyle {\boldsymbol {\hat {\beta }}}=\left(X^{\mathsf {T}}X\right)^{-1}X^{\mathsf {T}}Y} {\displaystyle {\boldsymbol {\hat {\beta }}}=\left(X^{\mathsf {T}}X\right)^{-1}X^{\mathsf {T}}Y}

Non-linear least squares

[edit]

There is, in some cases, a closed-form solution to a non-linear least squares problem – but in general there is not. In the case of no closed-form solution, numerical algorithms are used to find the value of the parameters β {\displaystyle \beta } {\displaystyle \beta } that minimizes the objective. Most algorithms involve choosing initial values for the parameters. Then, the parameters are refined iteratively, that is, the values are obtained by successive approximation: β j k + 1 = β j k + Δ β j , {\displaystyle {\beta _{j}}^{k+1}={\beta _{j}}^{k}+\Delta \beta _{j},} {\displaystyle {\beta _{j}}^{k+1}={\beta _{j}}^{k}+\Delta \beta _{j},}where a superscript k is an iteration number, and the vector of increments Δ β j {\displaystyle \Delta \beta _{j}} {\displaystyle \Delta \beta _{j}} is called the shift vector. In some commonly used algorithms, at each iteration the model may be linearized by approximation to a first-order Taylor series expansion about β k {\displaystyle {\boldsymbol {\beta }}^{k}} {\displaystyle {\boldsymbol {\beta }}^{k}}: f ( x i , β ) = f k ( x i , β ) + ∑ j ∂ f ( x i , β ) ∂ β j ( β j − β j k ) = f k ( x i , β ) + ∑ j J i j Δ β j . {\displaystyle {\begin{aligned}f(x_{i},{\boldsymbol {\beta }})&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}\left(\beta _{j}-{\beta _{j}}^{k}\right)\\[1ex]&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}J_{ij}\,\Delta \beta _{j}.\end{aligned}}} {\displaystyle {\begin{aligned}f(x_{i},{\boldsymbol {\beta }})&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}\left(\beta _{j}-{\beta _{j}}^{k}\right)\[1ex]&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}J_{ij}\,\Delta \beta _{j}.\end{aligned}}}

The Jacobian J is a function of constants, the independent variable and the parameters, so it changes from one iteration to the next. The residuals are given by r i = y i − f k ( x i , β ) − ∑ k = 1 m J i k Δ β k = Δ y i − ∑ j = 1 m J i j Δ β j . {\displaystyle r_{i}=y_{i}-f^{k}(x_{i},{\boldsymbol {\beta }})-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}=\Delta y_{i}-\sum _{j=1}^{m}J_{ij}\,\Delta \beta _{j}.} {\displaystyle r_{i}=y_{i}-f^{k}(x_{i},{\boldsymbol {\beta }})-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}=\Delta y_{i}-\sum _{j=1}^{m}J_{ij}\,\Delta \beta _{j}.}

To minimize the sum of squares of r i {\displaystyle r_{i}} {\displaystyle r_{i}}, the gradient equation is set to zero and solved for Δ β j {\displaystyle \Delta \beta _{j}} {\displaystyle \Delta \beta _{j}}: − 2 ∑ i = 1 n J i j ( Δ y i − ∑ k = 1 m J i k Δ β k ) = 0 , {\displaystyle -2\sum _{i=1}^{n}J_{ij}\left(\Delta y_{i}-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}\right)=0,} {\displaystyle -2\sum _{i=1}^{n}J_{ij}\left(\Delta y_{i}-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}\right)=0,}which, on rearrangement, become m simultaneous linear equations, the normal equations: ∑ i = 1 n ∑ k = 1 m J i j J i k Δ β k = ∑ i = 1 n J i j Δ y i ( j = 1 , … , m ) . {\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{m}J_{ij}J_{ik}\,\Delta \beta _{k}=\sum _{i=1}^{n}J_{ij}\,\Delta y_{i}\qquad (j=1,\ldots ,m).} {\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{m}J_{ij}J_{ik}\,\Delta \beta _{k}=\sum _{i=1}^{n}J_{ij}\,\Delta y_{i}\qquad (j=1,\ldots ,m).}

The normal equations are written in matrix notation as ( J T J ) Δ β = J T Δ y . {\displaystyle \left(\mathbf {J} ^{\mathsf {T}}\mathbf {J} \right)\Delta {\boldsymbol {\beta }}=\mathbf {J} ^{\mathsf {T}}\Delta \mathbf {y} .} {\displaystyle \left(\mathbf {J} ^{\mathsf {T}}\mathbf {J} \right)\Delta {\boldsymbol {\beta }}=\mathbf {J} ^{\mathsf {T}}\Delta \mathbf {y} .}

These are the defining equations of the Gauss–Newton algorithm.

Differences between linear and nonlinear least squares

[edit]

These differences must be considered whenever the solution to a nonlinear least squares problem is being sought.[12]

Consider a simple example drawn from physics. A spring should obey Hooke's law which states that the extension of a spring y is proportional to the force, F, applied to it. y = f ( F , k ) = k F {\displaystyle y=f(F,k)=kF} {\displaystyle y=f(F,k)=kF}constitutes the model, where F is the independent variable. In order to estimate the force constant, k, we conduct a series of n measurements with different forces to produce a set of data, ( F i , y i ) , i = 1 , … , n {\displaystyle (F_{i},y_{i}),\ i=1,\dots ,n\!} {\displaystyle (F_{i},y_{i}),\ i=1,\dots ,n\!}, where yi is a measured spring extension.[14] Each experimental observation will contain some error, ε {\displaystyle \varepsilon } {\displaystyle \varepsilon }, and so we may specify an empirical model for our observations, y i = k F i + ε i . {\displaystyle y_{i}=kF_{i}+\varepsilon _{i}.} {\displaystyle y_{i}=kF_{i}+\varepsilon _{i}.}

There are many methods we might use to estimate the unknown parameter k. Since the n equations in the m variables in our data comprise an overdetermined system with one unknown and n equations, we estimate k using least squares. The sum of squares to be minimized is[12] S = ∑ i = 1 n ( y i − k F i ) 2 . {\displaystyle S=\sum _{i=1}^{n}\left(y_{i}-kF_{i}\right)^{2}.} {\displaystyle S=\sum _{i=1}^{n}\left(y_{i}-kF_{i}\right)^{2}.}

The least squares estimate of the force constant, k, is given by k ^ = ∑ i F i y i ∑ i F i 2 . {\displaystyle {\hat {k}}={\frac {\sum _{i}F_{i}y_{i}}{\sum _{i}F_{i}^{2}}}.} {\displaystyle {\hat {k}}={\frac {\sum _{i}F_{i}y_{i}}{\sum _{i}F_{i}^{2}}}.}

We assume that applying force causes the spring to expand. After having derived the force constant by least squares fitting, we predict the extension from Hooke's law.

Uncertainty quantification

[edit]

In a least squares calculation with unit weights, or in linear regression, the variance on the j_th parameter, denoted var ⁡ ( β ^ j ) {\displaystyle \operatorname {var} ({\hat {\beta }}_{j})} {\displaystyle \operatorname {var} ({\hat {\beta }}_{j})}, is usually estimated with var ⁡ ( β ^ j ) = σ 2 ( [ X T X ] − 1 ) j j ≈ σ ^ 2 C j j , {\displaystyle \operatorname {var} ({\hat {\beta }}_{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{-1}\right)_{jj}\approx {\hat {\sigma }}^{2}C_{jj},} ![{\displaystyle \operatorname {var} ({\hat {\beta }}{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{-1}\right){jj}\approx {\hat {\sigma }}^{2}C{jj},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85cf89d392a9c191ff1fe3429654bd748a02b2b) σ ^ 2 ≈ S n − m {\displaystyle {\hat {\sigma }}^{2}\approx {\frac {S}{n-m}}} {\displaystyle {\hat {\sigma }}^{2}\approx {\frac {S}{n-m}}} C = ( X T X ) − 1 , {\displaystyle C=\left(X^{\mathsf {T}}X\right)^{-1},} {\displaystyle C=\left(X^{\mathsf {T}}X\right)^{-1},}where the true error variance _σ_2 is replaced by an estimate, the reduced chi-squared statistic, based on the minimized value of the residual sum of squares (objective function), S. The denominator, n − m, is the statistical degrees of freedom; see effective degrees of freedom for generalizations.[12] C is the covariance matrix.

Statistical testing

[edit]

If the probability distribution of the parameters is known or an asymptotic approximation is made, confidence limits can be found. Similarly, statistical tests on the residuals can be conducted if the probability distribution of the residuals is known or assumed. We can derive the probability distribution of any linear combination of the dependent variables if the probability distribution of experimental errors is known or assumed. Inferring is easy when assuming that the errors follow a normal distribution, consequently implying that the parameter estimates and residuals will also be normally distributed conditional on the values of the independent variables.[12]

It is necessary to make assumptions about the nature of the experimental errors to test the results statistically. A common assumption is that the errors belong to a normal distribution. The central limit theorem supports the idea that this is a good approximation in many cases.

However, suppose the errors are not normally distributed. In that case, a central limit theorem often nonetheless implies that the parameter estimates will be approximately normally distributed so long as the sample is reasonably large. For this reason, given the important property that the error mean is independent of the independent variables, the distribution of the error term is not an important issue in regression analysis. Specifically, it is not typically important whether the error term follows a normal distribution.

Weighted least squares

[edit]

"Fanning Out" Effect of Heteroscedasticity

A special case of generalized least squares called weighted least squares occurs when all the off-diagonal entries of Ω (the correlation matrix of the residuals) are null; the variances of the observations (along the covariance matrix diagonal) may still be unequal (heteroscedasticity). In simpler terms, heteroscedasticity is when the variance of Y i {\displaystyle Y_{i}} {\displaystyle Y_{i}} depends on the value of x i {\displaystyle x_{i}} {\displaystyle x_{i}} which causes the residual plot to create a "fanning out" effect towards larger Y i {\displaystyle Y_{i}} {\displaystyle Y_{i}} values as seen in the residual plot to the right. On the other hand, homoscedasticity is assuming that the variance of Y i {\displaystyle Y_{i}} {\displaystyle Y_{i}} and variance of U i {\displaystyle U_{i}} {\displaystyle U_{i}} are equal.[10]

Relationship to principal components

[edit]

The first principal component about the mean of a set of points can be represented by that line which most closely approaches the data points (as measured by squared distance of closest approach, i.e. perpendicular to the line). In contrast, linear least squares tries to minimize the distance in the y {\displaystyle y} {\displaystyle y} direction only. Thus, although the two use a similar error metric, linear least squares is a method that treats one dimension of the data preferentially, while PCA treats all dimensions equally.

Relationship to measure theory

[edit]

Notable statistician Sara van de Geer used empirical process theory and the Vapnik–Chervonenkis dimension to prove a least-squares estimator can be interpreted as a measure on the space of square-integrable functions.[16]

Tikhonov regularization

[edit]

In some contexts, a regularized version of the least squares solution may be preferable. Tikhonov regularization (or ridge regression) adds a constraint that ‖ β ‖ 2 2 {\displaystyle \left\|\beta \right\|_{2}^{2}} {\displaystyle \left\|\beta \right\|_{2}^{2}}, the squared ℓ 2 {\displaystyle \ell _{2}} {\displaystyle \ell _{2}}-norm of the parameter vector, is not greater than a given value to the least squares formulation, leading to a constrained minimization problem. This is equivalent to the unconstrained minimization problem where the objective function is the residual sum of squares plus a penalty term α ‖ β ‖ 2 2 {\displaystyle \alpha \left\|\beta \right\|_{2}^{2}} {\displaystyle \alpha \left\|\beta \right\|_{2}^{2}} and α {\displaystyle \alpha } {\displaystyle \alpha } is a tuning parameter (this is the Lagrangian form of the constrained minimization problem).[17]

In a Bayesian context, this is equivalent to placing a zero-mean normally distributed prior on the parameter vector.

An alternative regularized version of least squares is Lasso (least absolute shrinkage and selection operator), which uses the constraint that ‖ β ‖ 1 {\displaystyle \|\beta \|_{1}} {\displaystyle \|\beta \|_{1}}, the L1-norm of the parameter vector, is no greater than a given value.[18][19][20] (One can show like above using Lagrange multipliers that this is equivalent to an unconstrained minimization of the least-squares penalty with α ‖ β ‖ 1 {\displaystyle \alpha \|\beta \|_{1}} {\displaystyle \alpha \|\beta \|_{1}} added.) In a Bayesian context, this is equivalent to placing a zero-mean Laplace prior distribution on the parameter vector.[21] The optimization problem may be solved using quadratic programming or more general convex optimization methods, as well as by specific algorithms such as the least angle regression algorithm.

One of the prime differences between Lasso and ridge regression is that in ridge regression, as the penalty is increased, all parameters are reduced while still remaining non-zero, while in Lasso, increasing the penalty will cause more and more of the parameters to be driven to zero. This is an advantage of Lasso over ridge regression, as driving parameters to zero deselects the features from the regression. Thus, Lasso automatically selects more relevant features and discards the others, whereas Ridge regression never fully discards any features. Some feature selection techniques are developed based on the LASSO including Bolasso which bootstraps samples,[22] and FeaLect which analyzes the regression coefficients corresponding to different values of α {\displaystyle \alpha } {\displaystyle \alpha } to score all the features.[23]

The _L_1-regularized formulation is useful in some contexts due to its tendency to prefer solutions where more parameters are zero, which gives solutions that depend on fewer variables.[18] For this reason, the Lasso and its variants are fundamental to the field of compressed sensing. An extension of this approach is elastic net regularization.

  1. ^ Charnes, A.; Frome, E. L.; Yu, P. L. (1976). "The Equivalence of Generalized Least Squares and Maximum Likelihood Estimates in the Exponential Family". Journal of the American Statistical Association. 71 (353): 169–171. doi:10.1080/01621459.1976.10481508.
  2. ^ Mansfield Merriman, "A List of Writings Relating to the Method of Least Squares"
  3. ^ Bretscher, Otto (1995). Linear Algebra With Applications (3rd ed.). Upper Saddle River, NJ: Prentice Hall.
  4. ^ a b c Stigler, Stephen M. (1981). "Gauss and the Invention of Least Squares". Ann. Stat. 9 (3): 465–474. doi:10.1214/aos/1176345451.
  5. ^ Plackett, R.L. (1972). "The discovery of the method of least squares" (PDF). Biometrika. 59 (2): 239–251.
  6. ^ a b Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Cambridge, MA: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
  7. ^ Legendre, Adrien-Marie (1805), Nouvelles méthodes pour la détermination des orbites des comètes [_New Methods for the Determination of the Orbits of Comets_] (in French), Paris: F. Didot, hdl:2027/nyp.33433069112559
  8. ^ "The Discovery of Statistical Regression". Priceonomics. 2015-11-06. Retrieved 2023-04-04.
  9. ^ Aldrich, J. (1998). "Doing Least Squares: Perspectives from Gauss and Yule". International Statistical Review. 66 (1): 61–81. doi:10.1111/j.1751-5823.1998.tb00406.x. S2CID 121471194.
  10. ^ a b c d A modern introduction to probability and statistics: understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{[cite book](/wiki/Template:Cite%5Fbook "Template:Cite book")}}: CS1 maint: others (link)
  11. ^ For a good introduction to error-in-variables, please see Fuller, W. A. (1987). Measurement Error Models. John Wiley & Sons. ISBN 978-0-471-86187-4.
  12. ^ a b c d e f g h Williams, Jeffrey H. (Jeffrey Huw), 1956- (November 2016). Quantifying measurement: the tyranny of numbers. Morgan & Claypool Publishers, Institute of Physics (Great Britain). San Rafael [California] (40 Oak Drive, San Rafael, CA, 94903, USA). ISBN 978-1-68174-433-9. OCLC 962422324.{{[cite book](/wiki/Template:Cite%5Fbook "Template:Cite book")}}: CS1 maint: location (link) CS1 maint: location missing publisher (link) CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
  13. ^ a b Rencher, Alvin C.; Christensen, William F. (2012-08-15). Methods of Multivariate Analysis. John Wiley & Sons. p. 155. ISBN 978-1-118-39167-9.
  14. ^ Gere, James M.; Goodno, Barry J. (2013). Mechanics of Materials (8th ed.). Stamford, Conn.: Cengage Learning. ISBN 978-1-111-57773-5. OCLC 741541348.
  15. ^ Hallin, Marc (2012). "Gauss-Markov Theorem". Encyclopedia of Environmetrics. Wiley. doi:10.1002/9780470057339.vnn102. ISBN 978-0-471-89997-6. Retrieved 18 October 2023.
  16. ^ van de Geer, Sara (June 1987). "A New Approach to Least-Squares Estimation, with Applications". Annals of Statistics. 15 (2): 587–602. doi:10.1214/aos/1176350362. S2CID 123088844.
  17. ^ van Wieringen, Wessel N. (2021). "Lecture notes on ridge regression". arXiv:1509.09169 [stat.ME].
  18. ^ a b Tibshirani, R. (1996). "Regression shrinkage and selection via the lasso". Journal of the Royal Statistical Society, Series B. 58 (1): 267–288. JSTOR 2346178.
  19. ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome H. (2009). The Elements of Statistical Learning (second ed.). Springer-Verlag. ISBN 978-0-387-84858-7. Archived from the original on 2009-11-10.
  20. ^ Bühlmann, Peter; van de Geer, Sara (2011). Statistics for High-Dimensional Data: Methods, Theory and Applications. Springer. ISBN 9783642201929.
  21. ^ Park, Trevor; Casella, George (2008). "The Bayesian Lasso". Journal of the American Statistical Association. 103 (482): 681–686. doi:10.1198/016214508000000337. S2CID 11797924.
  22. ^ Bach, Francis R (2008). "Bolasso". Proceedings of the 25th international conference on Machine learning - ICML '08. pp. 33–40. arXiv:0804.1302. Bibcode:2008arXiv0804.1302B. doi:10.1145/1390156.1390161. ISBN 9781605582054. S2CID 609778.
  23. ^ Zare, Habil (2013). "Scoring relevancy of features based on combinatorial analysis of Lasso with application to lymphoma diagnosis". BMC Genomics. 14 (Suppl 1): S14. doi:10.1186/1471-2164-14-S1-S14. PMC 3549810. PMID 23369194.