Order-4 pentagonal tiling (original) (raw)
From Wikipedia, the free encyclopedia
Regular tiling of the hyperbolic plane
| Order-4 pentagonal tiling | ||
|---|---|---|
 Poincaré disk model of the hyperbolic plane Poincaré disk model of the hyperbolic plane |
||
| Type | Hyperbolic regular tiling | |
| Vertex configuration | 54 | |
| Schläfli symbol | {5,4}r{5,5} or { 5 5 } {\displaystyle {\begin{Bmatrix}5\\5\end{Bmatrix}}}  |
|
| Wythoff symbol | 4 | 5 22 | 5 5 |
| Coxeter diagram |           or or    |
|
| Symmetry group | [5,4], (*542)[5,5], (*552) | |
| Dual | Order-5 square tiling | |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the order-4 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,4}. It can also be called a pentapentagonal tiling in a bicolored quasiregular form.
This tiling represents a hyperbolic kaleidoscope of 5 mirrors meeting as edges of a regular pentagon. This symmetry by orbifold notation is called *22222 with 5 order-2 mirror intersections. In Coxeter notation can be represented as [5*,4], removing two of three mirrors (passing through the pentagon center) in the [5,4] symmetry.
The kaleidoscopic domains can be seen as bicolored pentagons, representing mirror images of the fundamental domain. This coloring represents the uniform tiling t1{5,5} and as a quasiregular tiling is called a pentapentagonal tiling.
| Uniform pentagonal/square tilings vte | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [5,4], (*542) | [5,4]+, (542) | [5+,4], (5*2) | [5,4,1+], (*552) | ||||||
     |
     |
     |
     |
     |
     |
     |
     |
     |
     |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} |
| Uniform duals | |||||||||
     |
     |
     |
     |
     |
     |
     |
     |
     |
     |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V45 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V55 |
| Uniform pentapentagonal tilings vte | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,5], (*552) | [5,5]+, (552) | ||||||
     = =      |
     = =      |
     = =      |
     = =      |
     = =      |
     = =      |
     = =      |
     = =      |
 |
 |
 |
 |
 |
 |
 |
 |
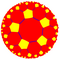
| Order-5 pentagonal tiling {5,5} | Truncated order-5 pentagonal tiling t{5,5} | Order-4 pentagonal tiling r{5,5} | Truncated order-5 pentagonal tiling 2t{5,5} = t{5,5} | Order-5 pentagonal tiling 2r{5,5} = {5,5} | Tetrapentagonal tiling rr{5,5} | Truncated order-4 pentagonal tiling tr{5,5} | Snub pentapentagonal tiling sr{5,5} |
| Uniform duals | |||||||
     |
     |
     |
     |
     |
     |
     |
     |
 |
 |
 |
 |
 |
 |
 |
|
| Order-5 pentagonal tiling V5.5.5.5.5 | V5.10.10 | Order-5 square tiling V5.5.5.5 | V5.10.10 | Order-5 pentagonal tiling V5.5.5.5.5 | V4.5.4.5 | V4.10.10 | V3.3.5.3.5 |
This tiling is topologically related as a part of sequence of regular polyhedra and tilings with pentagonal faces, starting with the dodecahedron, with Schläfli symbol {5,n}, and Coxeter diagram 



 , progressing to infinity.
, progressing to infinity.
| {5,n} tilings | ||||
|---|---|---|---|---|
 {5,3} {5,3}     |
 {5,4} {5,4}     |
 {5,5} {5,5}     |
 {5,6} {5,6}     |
 {5,7} {5,7}     |
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram 



 , with n progressing to infinity.
, with n progressing to infinity.
| *_n_42 symmetry mutation of regular tilings: {n,4} vte | |||||||
|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | |||||
 |
 |
 |
 |
 |
 |
 |
 |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
This tiling is topologically related as a part of sequence of regular polyhedra and tilings with vertex figure (4n).
| *_n_42 symmetry mutation of regular tilings: {4,n} vte | ||||||
|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperbolic | Paracompact | |||
 {4,3} {4,3}     |
 {4,4} {4,4}     |
 {4,5} {4,5}     |
 {4,6} {4,6}     |
 {4,7} {4,7}     |
 {4,8}... {4,8}...     |
 {4,∞} {4,∞}     |
| *5_n_2 symmetry mutations of quasiregular tilings: (5.n)2 vte | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry*5_n_2[n,5] | Spherical | Hyperbolic | Paracompact | Noncompact | ||||
| *352[3,5] | *452[4,5] | *552[5,5] | *652[6,5] | *752[7,5] | *852[8,5]... | *∞52[∞,5] | [_n_i,5] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
|
| Config. | (5.3)2 | (5.4)2 | (5.5)2 | (5.6)2 | (5.7)2 | (5.8)2 | (5.∞)2 | (5._n_i)2 |
| Rhombicfigures |  |
 |
 |
 |
||||
| Config. | V(5.3)2 | V(5.4)2 | V(5.5)2 | V(5.6)2 | V(5.7)2 | V(5.8)2 | V(5.∞)2 | V(5.∞)2 |
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- Coxeter, H. S. M. (1999), Chapter 10: Regular honeycombs in hyperbolic space (PDF), The Beauty of Geometry: Twelve Essays, Dover Publications, ISBN 0-486-40919-8, LCCN 99035678, archived from the original (PDF) on 2016-06-10, retrieved 2017-02-19, invited lecture, ICM, Amsterdam, 1954.
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
