Hyperbolic Tiling (original) (raw)
Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology
Alphabetical Index New in MathWorld
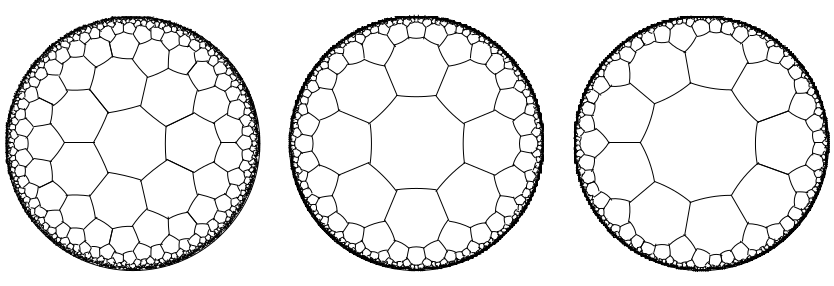
The illustrations above show a number of hyperbolic tilings, including the heptagonal once related to the Klein quartic.
Escher was fond of depicting hyperbolic tilings, including "Circle Limit I" (Bool et al. 1982, p. 319), "Circle Limit III" (Bool et al. 1982, pp. 97 and 320), and "Circle Limit IV" (Bool _et al._1982, pp. 98 and 322).
See also
Apeirogon, Euclidean Plane, Hyperbolic Plane, Klein Quartic, Poincaré Hyperbolic Disk,Riemann Sphere, Rigid Motion
Explore with Wolfram|Alpha
References
Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F. M. C. Escher: His Life and Complete Graphic Work. New York: Abrams, 1982.Escher, M. C. "Circle Limit III." Woodcut, printed from 5 blocks. 1959a. http://www.mcescher.com/Gallery/recogn-bmp/LW434.jpg.Escher, M. C. "Circle Limit IV." Woodcut, printed from 2 blocks. 1959b. http://www.mcescher.com/Gallery/recogn-bmp/LW436.jpg.Hatch, D. "Hyperbolic Planar Tessellations." http://www.plunk.org/~hatch/HyperbolicTesselations/.
Referenced on Wolfram|Alpha
Cite this as:
Weisstein, Eric W. "Hyperbolic Tiling." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/HyperbolicTiling.html