Maths - Projections of lines on planes (original) (raw)

We want to find the component of line A that is projected onto plane B and the component of line A that is projected onto the normal of the plane.

We have covered projections of lines on lines here.

The orientation of the plane is defined by its normal vector B as described here.

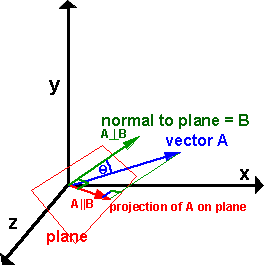
To do this we will use the following notation:

• A || B = the component of line A that is projected onto plane B, in other words a vector to the point on the plane where, if you take a normal at that point, it will intercept the end of vector A.
• A 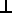B = the component of line A is projected onto the normal of plane B.

We will also use:

• |A| = the scalar magnitude of vector A.
• θ = the angle between vector A and the normal to plane B
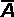• = a unit vector in the direction of A

So: 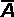= A / |A|

Relationship between these quantities

If we add the the parallel and perpendicular components then we get the original vector, which gives us the following equation:

A = A || B + A 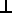B

So if we have the perpendicular component we can work out the parallel component and visa-versa.

Calculation of the projection on the plane

From the above diagram, the scalar magnitude of the projection on the plane is |A| sin(θ) and its direction is along the plane (which is perpendicular to the normal B).

To find the direction that we want, first take a vector which is mutually perpendicular to A and B, this is given by the cross product A x B (which is out of the page on the above diagram). Now take a vector which is mutually perpendicular to this and vector B, this gives us the direction that we want.

So the direction is:

B × (A × B)

or: (B × A) × B

We need to normalise this, so a unit vector in the required direction is:

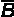x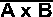

From the diagram above the magnitude of the projection on the plane is:

|A| sin(θ)

So the projection on the plane is:

A || B = |A| sin(θ) ×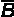

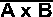
But from this page we know that: 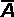× 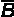= 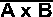sin(θ) so:

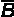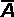A || B = |A| x x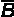

but 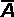= A / |A| and 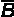= B / |B|

so:

A || B = B × (A×B / |B|) / |B

Calculation of the perpendicular component

|From the above diagram, the scalar magnitude of the perpendicular component is |A| cos(θ) and its direction is in the direction of vector B. So if we multiply |A| cos(θ) by a unit vector along B, which is, B/|B|

So the vector we want is:

A 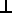B = |A| cos(θ) * B/|B|

We can use the vector dot product to calculate this, from this page we know that:

A•B = |A| |B| cos(θ)

Therefore combining these equations gives:

A 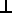B = A•B * B/|B|2

Alternative using Clifford or Geometric Algebra

For information about Clifford/Geometric Algebra see here. In Geometric algebra are represented by bivectors.

In this case:

• A is a vector
• B is a bivector (representing the plane)

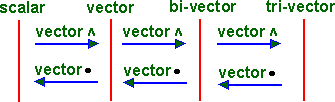
Outer product

This is the geometric algebra equivalent of the cross product, but it is not limited to multiplying vectors by vectors, it increases to grade of operand as follows:

• scalar 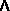vector = vector
• vector 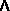vector = bivector
• bivector 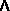vector = tri-vector

Inner product

This is the geometric algebra equivalent of the dot product, but it is not limited to multiplying vectors by vectors, it decreases to grade of operand as follows:

• vector • vector = scalar
• bivector • vector = vector
• tri-vector • vector = bivector

So the inner and outer products are symmetrical as follows:

For the projection of line on line we had:

In this case we can use exactly the same equations but B is now represented by a bivector.

Alternative using Matrix representation

(My original working is on this page before Xavier pointed out the inconsistencies)

Starting with the vector algebra equations derived above we have:

parallel component = A || B = B × (A × B) / |B|²

perpendicular component =A B = A•B * B / |B|²

To convert these from vector to matrix equations we can use the following matrix equivalents of the cross and dot products:

To replace the cross product we can use the skew symmetric matrix as described on this page:

| B×A = [~B][A] = | 0 -Bz By Bz 0 -Bx -By Bx 0 | | | -------------------- | ----------------------------- | |

To replace the dot product the result needs to be a scalar (or a 1×1 matrix which we can get by multiplying by the transpose of B or alternatively just multiply by the scalar factor: (Ax * Bx + Ay * By + Az * Bz)

perpendicular component

So lets work out the full terms for the perpendicular component:

| A 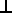B = A•B * B / |B|² = | Bx * (Ax * Bx + Ay * By + Az * Bz) /(Bx² + By² + Bz²) By * (Ax * Bx + Ay * By + Az * Bz) /(Bx² + By² + Bz²) Bz * (Ax * Bx + Ay * By + Az * Bz) /(Bx² + By² + Bz²) | | ----------------------------------------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |

Assuming B is normalised (Bx² + By² + Bz²=1) and separating out A and B gives:

A 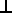B =	Bx² Bx*By Bx*Bz By*Bx By² By*Bz Bz*Bx Bz*By Bz²

parallel component

We can work out the parallel component in terms of matricies:

A || B = B × (A × B) / |B|²

The cross product anticommutes, that is reversing the order of the operands changes the sign, so we get:

A || B = - B × (B × A) / |B|²

Convert ing this into a matrix equation using the skew symmetric matrix as described above gives:

A || B = - [~B][~B][A] / |B|²

Whiting out the terms:

| A || B = - | 0 -Bz By Bz 0 -Bx -By Bx 0 | 0 -Bz By Bz 0 -Bx -By Bx 0 | /(Bx² + By² + Bz²) | | ----------- | ----------------------------- | ----------------------------- | ------------------ |

Assuming B is normalised (Bx² + By² + Bz²=1) and multiplying out the two skew matrix terms gives:

| A || B = - | -Bz² - By² Bx*By Bx*Bz By*Bx -Bz² - Bx² By*Bz Bz*Bx Bz*By -Bx² - By² | | ----------- | ----------------------------------------------------------------------------- |

Puting the leading '-' term into the matrix gives:

| A || B = | Bz² + By² -Bx*By -Bx*Bz -By*Bx Bz² + Bx² -By*Bz -Bz*Bx -Bz*By Bx² + By² | | --------- | ----------------------------------------------------------------------------------- |

using (Bx² + By² + Bz²=1) again on the leading diagonal:

| A || B = | 1 - Bx² -Bx*By -Bx*Bz -By*Bx 1 - By² -By*Bz -Bz*Bx -Bz*By 1 - Bz² | | --------- | ----------------------------------------------------------------------------- |

check on result

We can check the above results because the perpendicular and parallel components should add to give the original vector A, in other words:

A = A || B + A 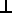B

Substituting the matrix values:

| A || B + A 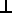B | 1 - Bx² + Bx² -Bx*By + Bx*By -Bx*Bz+Bx*Bz -By*Bx+By*Bx 1 - By² + By² -By*Bz+By*Bz -Bz*Bx + Bz*Bx -Bz*By+Bz*By 1 - Bz²+ Bz² | | ------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------------------------------------------------------------------------------- |

Canceling out equal and opposite values gives:

| A || B + A B | | ------------------------------------------------------------------------------------------------------------------- |

Therefore the B part reduces to the identity matrix [I] and we are left with the vector A which is what we want.

Further Reading

We can use this to do reflections as shown here:

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.