Mixture models for single-cell assays with applications to vaccine studies (original) (raw)

Abstract

Blood and tissue are composed of many functionally distinct cell subsets. In immunological studies, these can be measured accurately only using single-cell assays. The characterization of these small cell subsets is crucial to decipher system-level biological changes. For this reason, an increasing number of studies rely on assays that provide single-cell measurements of multiple genes and proteins from bulk cell samples. A common problem in the analysis of such data is to identify biomarkers (or combinations of biomarkers) that are differentially expressed between two biological conditions (e.g. before/after stimulation), where expression is defined as the proportion of cells expressing that biomarker (or biomarker combination) in the cell subset(s) of interest. Here, we present a Bayesian hierarchical framework based on a beta-binomial mixture model for testing for differential biomarker expression using single-cell assays. Our model allows the inference to be subject specific, as is typically required when assessing vaccine responses, while borrowing strength across subjects through common prior distributions. We propose two approaches for parameter estimation: an empirical-Bayes approach using an Expectation–Maximization algorithm and a fully Bayesian one based on a Markov chain Monte Carlo algorithm. We compare our method against classical approaches for single-cell assays including Fisher’s exact test, a likelihood ratio test, and basic log-fold changes. Using several experimental assays measuring proteins or genes at single-cell level and simulations, we show that our method has higher sensitivity and specificity than alternative methods. Additional simulations show that our framework is also robust to model misspecification. Finally, we demonstrate how our approach can be extended to testing multivariate differential expression across multiple biomarker combinations using a Dirichlet-multinomial model and illustrate this approach using single-cell gene expression data and simulations.

Keywords: Bayesian modeling, Expectation–Maximization, Flow cytometry, Hierarchical modeling, Immunology, Marginal likelihood, Markov Chain Monte Carlo, MIMOSA, Single-cell gene expression

1. Introduction

Cell populations, particularly in the immune system, are never truly homogeneous. Individual cells may be in different biochemical states that define functional but measurable differences between them. This single-cell heterogeneity is informative, but lost in assays that measure cell mixtures (e.g. bulk gene expression). For this reason, single-cell assays (e.g. flow, mass cytometry, single-cell gene expression) are an important tool in immunology, providing a functional snapshot of the immune system at a given time. These assays typically measure multiple biomarkers (e.g. DNA content, RNA or protein expression levels, or protein phosphorylation) simultaneously on individual cells in a heterogeneous mixture such as whole blood or peripheral blood mononuclear cells, and are used for immune monitoring of disease, vaccine research, and diagnosis of hematological malignancies (Altman and others, 1996; Betts and others, 2006; Inokuma and others, 2007). McDavid and others (2012) review the special considerations for analyzing single-cell assay data. In general, special treatment of single-cell level data is warranted in order to preserve information about cell population heterogeneity.

Typically, cell-level measurements are thresholded as positive or negative so that subsets with different multivariate +/− biomarkers can be obtained as Boolean combinations. For some assays (e.g. flow cytometry), the positivity thresholds are set based on prior biological knowledge while for others, thresholds are given by the assay technology. This is the case for the Fluidigm’s qPCR-based single-cell gene expression technology, where genes are recorded as expressed or not, at single-cell level (McDavid and others, 2012). 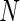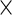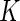After thresholding, we obtain a Boolean matrix of cells biomarkers and we can form 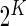putative cell subsets. When 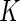is large, there is a combinatorial explosion of the number of subsets, and many of these might be small or even empty. A common statistical problem is to identify subjects for whom the proportion of cells expressing a specific combination is significantly different between two experimental conditions (e.g. before and after stimulation).

A motivating example from vaccine research is the need to assess the immunogenicity of a vaccine. Upon vaccination, antigen in the vaccine is taken up and presented to CD4 or CD8 T-cells via antigen presenting cells. T-cells that recognize the antigen become activated, produce cytokines that potentiate the immune response, and proliferate and persist in the immune system providing memory that can more rapidly recognize the same antigen in the future (McKinstry and others, 2010). This vaccine memory can be interrogated through the intracellular cytokine staining (ICS) assay, by measuring antigen-specific cytokine production in response to stimulation (Horton and others, 2007; De Rosa and others, 2004; Betts and others, 2006). The antigen-specific subpopulations constitute a small fraction of the total number of CD4 and CD8 T-cells (as low as 0.01–0.1%), and a large number of cells must be collected (on the order of 50 000–100 000 T-cells) to ensure that changes in these cell populations can be reliably detected. Then, each individual cell is classified as either positive or negative for each cytokine based on fixed thresholds, and the number of cells matching each phenotype is counted.

Cell counts are compared between antigen-stimulated and unstimulated samples from a subject to identify significant differences. Responders are subjects whose T-cells respond to stimulation, and the response is vaccine-specific if it exists at the post-vaccine time point but not at the pre-vaccine time point. These comparisons are typically performed within a time point in order to avoid confounding vaccine effects with time of visit and because baseline samples are not always available.

Although there is no standard approach to analyzing ICS assays, current methods range from ad hoc rules based on log-fold changes (Trigona and others, 2003), to non-parametric methods (Sinclair and others, 2004), to exact tests of 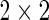contingency tables (e.g. Fisher’s exact test and 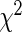test) (Horton and others, 2007; Proschan and Nason, 2009; Peiperl and others, 2010; Nason, 2006). All of these methods test subjects separately, and no information is shared across observations even though one could expect some similarities across responders (or non-responders).

The framework developed in this paper, named MIMOSA (Mixture Models for Single-Cell Assays), addresses these issues. In our model, cell counts are modeled by a binomial (or multinomial in the multivariate case) distribution and information is shared across subjects through a prior distribution on the unknown proportion(s) of the binomial (or multinomial) likelihood. In order to discriminate between responders and non-responders, the prior is written as a mixture of two beta (or Dirichlet) distributions where the hyper-parameters for each mixture component are shared across subjects. This sharing of information helps regularize proportion estimates when the cell counts are small, which is typical with the single-cell assays considered here, and increases sensitivity and specificity when detecting responders. Note that we use the term “subject” throughout the paper, but the approaches described are general and can be applied to other experimental units. Because our framework is multivariate in nature, multiple cell subsets can be modeled simultaneously, which could help detect small biological changes that are spread out across multiple cell subsets (Nason, 2006). Our paper is organized as follows. Section 2 introduces the data and notation used in the paper. In Section 3, we present our model for testing differential biomarker expression in the univariate case. Section 4 compares our approach to alternative methods and tests the robustness of our model. In Section 5, we present a multivariate extension that can be used to test multivariate biomarker differential expression and present results using single-cell gene expression data. Finally, in Section 6 we discuss our findings and future work.

2. Notation and data

We consider two types of immunological single-cell assays.

Flow cytometry: Our primary dataset is ICS data generated as part of a trial testing the GeoVax DNA and MVA (Modified Vaccinia Ankara) HIV vaccine in a prime-boost regimen (Goepfert and others, 2011). The study goal was to assess the immunogenicity of different prime-boost regimens. Here, we analyze a subset of the data consisting of 98 vaccine and placebo recipients at days 0 (pre-vaccine) and 182 (2 weeks post-vaccine), focusing on CD4+ T-cell response to stimulation with HIV Envelope peptide. Three cytokines (IFN-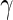, TNF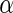, and IL2) were measured for each subject and time point, each with and without antigen stimulation. No response is expected at day 0, while day 182 is close to the immunogenicity peak and many vaccinees are expected to respond for at least some cytokines. A median of 51 and 58K T-cells were collected for the stimulated and unstimulated samples, respectively (IQR 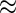37 and 43K, respectively). The empirical differences in the proportions of stimulated and unstimulated cells were on the order of 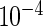, with the number of positive cells typically ranging from 1 to 70, depending on cytokine subset.

Fluidigm single-cell gene expression: Tetramer-sorted CD8+ T-cells from 16 subjects. T-cells isolated by flow cytometry from 16 subjects were stimulated in blocks of 4 subjects with 4 different antigens (HIV Gag, HIV Nef, CMV pp65 tm10, and CMV pp65 nlv5) and gene expression post-stimulation was measured at single-cell level, using the BioMark system (Fluidigm) 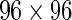well arrays. The expression from stimulated samples was compared with that from paired, unstimulated controls. In this data set, we have approximately 90 single cells per subject per stimulation condition with 96 gene expression measurements per cell.

3. Differential expression with one biomarker

Datasets like those presented here are usually analyzed in a univariate fashion to avoid being underpowered due to the large number of combinations and the potential for very small cell counts in many combinations. By univariate, we mean that we have only one positive cell subset. This cell subset can be defined by considering the expression of one biomarker alone (marginalizing over all other measured biomarkers) such as A+ (vs. A), or considering a specific positive biomarker combination (and marginalizing over everything else) such as A+ OR B+ (vs. A/B). Without loss of generality, we treat the univariate case as a one-biomarker case (i.e. 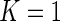). In this case, for a given subject, the data can be summarized in a contingency table of +/− cell counts across the unstimulated and stimulated samples (Table 1).

Table 1.

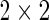contingency table of counts for biomarker positive and negative cells between stimulated 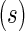and unstimulated 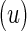conditions for a given subject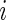

For a given subject and stimulation, we consider a biomarker to be differentially expressed if the proportion of positive cells in the stimulated samples is different from the proportion of positive cells in the unstimulated sample. Subjects that show differential expression will be called responders for that biomarker. In this section, we are concerned with identifying differential expression one biomarker at a time, using a beta-binomial mixture model.

3.1. Beta-binomial model

We use the following notation to describe our model. We assume that we observe cell counts from 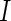subjects in two conditions: stimulated and unstimulated. Each cell can either be positive or negative for a biomarker. Given a set of 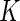biomarkers, the measured cells can be classified into 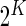Boolean combinations. We denote by 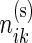and 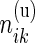, , 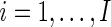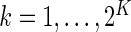be the observed counts for the 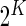combinations in the stimulated and unstimulated samples, respectively. We denote by 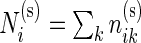and 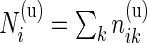the total number of cells measured for subject 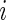in each sample. For ease of notation, we denote by 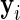the vector of observed counts for subject 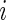, that is, 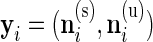where 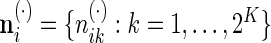, and finally .

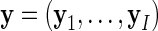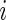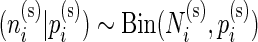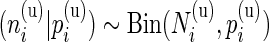For a given subject , the positive cell counts for the stimulated and unstimulated samples are jointly modeled as and , where 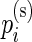, 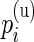are the unknown proportions for the stimulated and unstimulated paired samples, respectively. In order to detect responding subjects, we consider two competing models, 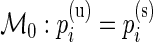and 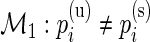. Under the null model, 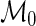, there is no difference between the stimulated and unstimulated samples, and the proportions are equal (yet the cell counts can differ). Under the alternative model, 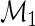, there is a difference in proportions between the two samples and the subject 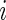is a responder. In some studies, such as the ICS data used here, the proportion of positive cells is expected to only increase after stimulation, in which case the alternative model should be defined as 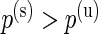. This alternative parameterization is described in Appendix A of supplementary material available at Biostatistics online, and we refer to it as the one-sided model.

3.2. Priors

Our model shares information across all subjects using exchangeable Beta priors on the unknown proportions. For non-responders, (p(u)i|z i_=0)∼_Beta(α(u),β(u)), and for responders (p(u)i|z _i_=1)∼Beta(α(u),β(u)) and (p(s)i|z _i_=1)∼Beta(α(s),β(s)), where z i is an indicator variable equal to one if subject 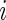is a responder, that is, 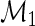is true, and zero otherwise, and α(u),β(u),α(s),β(s) are unknown hyper-parameters shared across all subjects. Note that the parameters α(u) and β(u) are shared across both models, whereas 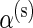and 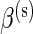are only present in the alternative model. Finally, we assume that 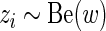are independent draws from a Bernoulli distribution with probability 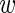, where 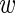represents the (unknown) proportion of responders. 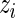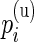It follows that marginally, that is, after integrating , the and 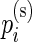are then jointly distributed as a mixture of a 1D beta distribution and a product of two beta distributions (with a possible constraint), with mixing parameter 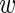. Treating the 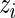’s as missing data, the unknown parameter vector **θ**≡(α(u),β(u),α(s),β(s),w) can be estimated in an empirical-Bayes fashion using an Expectation–Maximization (EM) algorithm (Dempster and others, 1977) as described in Section 3.3. We also describe a fully Bayesian model where the hyperparameters 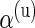, , 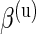, 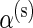and β(s) are each given vague exponential priors with mean 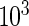, and 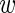is assumed to be drawn from a uniform distribution between 0 and 1. In this case, all parameters will be estimated via a Markov chain Monte Carlo (MCMC) algorithm as described in Section 3.3.

3.3. Parameter estimation

In our proposed EM and MCMC algorithms, we greatly simplify our calculations by directly utilizing the marginal likelihoods, 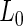and 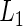, obtained after marginalizing 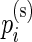and 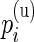from the null and alternative likelihoods. Given the conjugacy of the priors, the marginal likelihoods 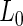and 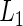are available in closed-forms (Appendix B of supplementary material available at Biostatistics online).

Assuming that the missing data, 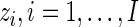, are known, we define the complete data log-likelihood:

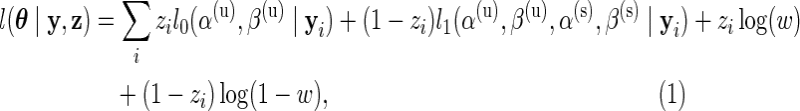	(3.1)

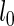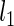where and are the log marginal-likelihoods and **θ**≡(α(u),β(u),α(s),β(s),w) is the vector of parameters to be estimated. In the one-sided case, the alternative prior specification must satisfy the constraint 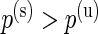, and the marginal likelihood derivation involves the calculation of a normalizing constant that is not available in closed-form but can easily be estimated. All calculations for the one-sided case are described in Appendix A of supplementary material available at Biostatistics online.

EM algorithm: Given an estimate of the model parameter vector 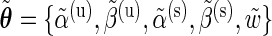and the data 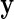, the E step consists in calculating the posterior probabilities of differential expression, defined by :

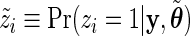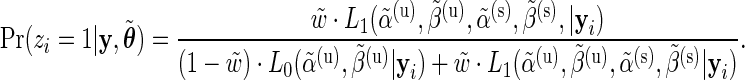
The M-step then consists in optimizing the complete-data log-likelihood over 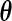after replacing 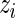by 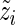in (3.1). Straightforward calculations lead to 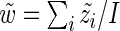, but unfortunately no closed form solutions exist for the remaining parameters. We use numerical optimization as implemented in R’s optim function to estimate the remaining parameters (Ihaka and Gentleman, 1996). We initialize the ’s using Fisher’s exact test to assign each observation to either the null or alternative components and then use the estimated 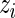’s to estimate the 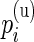’s and 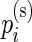’s and use these to set the hyper-parameters to their method-of-moments estimates.

MCMC algorithm: We generated realizations from the posterior distribution via MCMC algorithms (Gelfand and Smith, 1990). All updates were done via Metropolis–Hastings sampling except for the 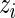’s and 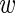that were performed via Gibbs sampling. Details about the algorithms and implementation are given in Appendix B of supplementary material available at Biostatistics online.

4. Results

We evaluated and compared the performance of MIMOSA against Fisher’s exact test, a likelihood ratio test, and log fold-change by receiver operator characteristic (ROC) curve analysis and by comparing the observed false discovery rate (FDR) against the nominal FDR (expected FDR) for the ICS data. A false discovery is defined as a day 0 sample or a sample from a placebo recipient (expected non-responders) that is identified as a responder by an algorithm. For MIMOSA, the FDR was computed using the approach of Newton and others (2004), whereas for all other methods FDR control was done using the approach of Benjamini and Hochberg (1995). The posterior mean of the 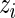was used for ranking the results in the FDR calculations.

4.1. Intracellular cytokine staining

In applying the MIMOSA model to the ICS data set, we fit a separate model for each cytokine subset (and each stimulation if we had analyzed more than one). We do not compare pre-vaccination and post-vaccination time points against each other directly. Rather, we have paired samples for each time points with the corresponding negative controls. Observations within each time point are contrasted against the corresponding negative controls, and we fit the model to observations from all time points simultaneously. Consequently, all time points that are fitted simultaneously will contribute to the priors for p(u). A subsequent evaluation of pre- and post-vaccination time points would involve comparing the positivity calls for paired samples at the two-time points. However, data are not typically analyzed this way, as this could lead to confounding of date with vaccine effect (i.e. batch effects). Furthermore, vaccine trials do not always collect baseline samples.

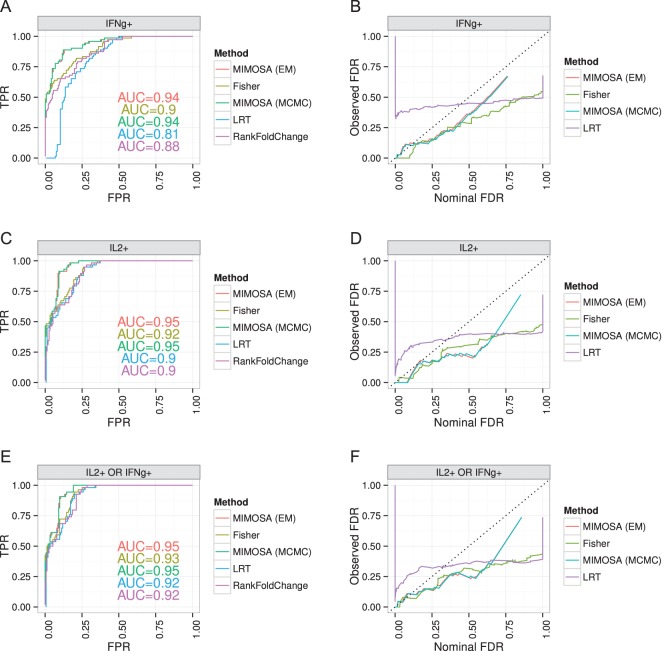
Within this framework, we considered observations from vaccinees at day 0 or from placebos at day 0 or 182 as true negatives in that we do not expect to observe a response in those samples. Observations from vaccinees at day 182 were considered true positives in that a response is expected assuming a 100% response rate. This assumption was required, since we do not have independent, external measurement of the true response. Under these assumptions, the MIMOSA model has higher sensitivity and specificity than the method compared here for discriminating vaccine responders and non-responders as shown by the ROC curves on Figures 1(A), (C), and (E). At an FDR between 10% and 20%, MIMOSA would lead to about 20% more true positives being detected. In addition, MIMOSA gave estimates of the observed FDR that are better or comparable with those in competing methods (Figures 1(B), (D), and (F)). Here, we present the results based on IL2 and IFN-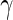 alone as well as the subset expressing IL2 OR IFN- 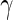that were used in the original study (Goepfert and others, 2011). These results are consistent for other cytokines and cytokine combinations, including higher order combinations ( Figure 1 of supplementary material available at Biostatistics online). We also evaluated, through simulation, what would happen to the ROC curves when our assumption of 100% response rate was false (i.e. when not all day 182 vaccinees are responders, Figure 2 of supplementary material available at Biostatistics online), and found that we are potentially underestimating the sensitivity of all methods considered here due to non-responders at day 182. Nonetheless, the ranking of the methods remained consistent and the conclusions from the ROC analysis still hold.

Figure 1.

Performance of the MIMOSA model (EM and MCMC implementations, one-sided) and competing methods on ICS flow cytometry data. Sensitivity and specificity (measured by ROC analysis) of each method, as well as a comparison of the observed and nominal false discovery rates for response calls from CD4+ T-cells stimulated with different antigens. (A and B) ENV-1-PTEG stimulated T-cells expressing IFN-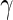, (C and D) expressing IL2. (E and F) expressing IFN- 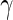OR IL2. ROC and FDR plots of other cytokine combinations can be found in Figure 1 of supplementary material available at Biostatistics online. This figure appears in color in the electronic version of this article.

We verified the assumption of a common distribution for the 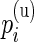across subjects by examining the empirical estimates of 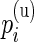and the density of the Beta distribution with parameters 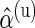, 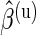fitted to ENV-1-PTEG stimulated CD4+/IFN- 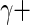T-cell ICS data (Figure 3 of supplementary material available at Biostatistics online). The effect of information sharing on the sensitivity and specificity of the model was also investigated by varying the number of subjects in simulations (Figure 4 of supplementary material available at Biostatistics online). Our model performed well when as few as 20 subjects were included, although the nominal FDR overestimated observed FDR.

4.2. Single-cell gene expression

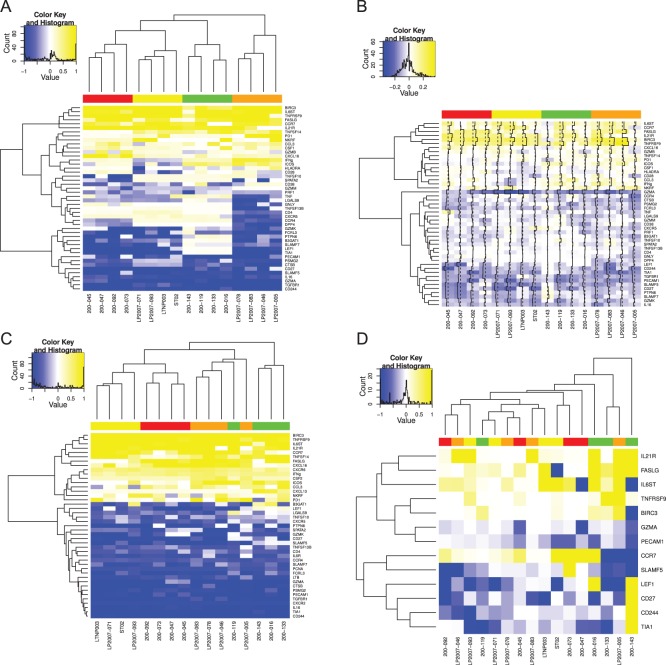
We applied the MIMOSA model to the Fluidigm single-cell gene expression data set. We used the two-sided MIMOSA model because genes could be regulated upward or downward upon stimulation. In order to detect stimulation-specific changes of expression, we fit our model separately to each gene within each stimulation. The results show that MIMOSA identifies stimulation-specific differences in the proportions of cells expressing each gene while preserving inter-subject variability (Figure 2(A)). These patterns evident in the posterior probabilities (Figure 2(A)) closely match the empirical estimates of the differences in proportions (Figure 2(B)). For comparison, we also fit the model combining information across all stimulations (Figure 2(C)). Although this leads to a sensible clustering by stimulation, the observed pattern does not agree as well with the empirical differences. A similar analysis applying a two-sided Fisher’s exact test to each sample and gene and clustering the signed FDR adjust 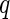-values (Figure 2(D)) does not reveal stimulation-specific patterns, with the exception of CMV pp65 nlv5 stimulation. We note that the differences in the clustering are not surprising, given that the MIMOSA model is sharing information across subjects within a stimulation. At an FDR of 10%, Fisher’s exact test identified 13 significant genes, while MIMOSA identified 46 significant genes. The 13 genes identified by Fisher’s method were a subset of those identified by MIMOSA. These results suggest that fitting a stimulation-specific model is the right approach, since information is shared across subjects that are expected to exhibit similar behavior.

Figure 2.

Signed posterior probability and difference in empirical in proportions of single-cells expressing each gene on a 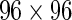Fluidigm array. The posterior probability of response times the sign of the change in expression is shown in (A) (red indicates a decrease, green an increase, relative to the control) for a model fit to each stimulation and gene separately. Columns and rows are clustered based on these signed posterior probabilities. (B) The empirical differences in proportion of cells expressing a gene in the stimulated vs. control samples. Rows and columns are ordered as in (A) for comparison. The traces show the deviations of each cell from zero. Colors along the columns denote different stimulations (green, CMV pp65 nlv5; red, HIV Gag; orange, HIV Nef; yellow, CMV pp65 tm10). (C) Signed posterior probabilities for a model fit per gene but across all stimulations simultaneously. (D) Clustering of the signed 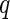-values from Fisher’s exact test. The differences in clustering are not surprising, given that the MIMOSA model shares information within stimulation. All genes were significant at, or below, the 10% FDR level. This figure appears in color in the electronic version of this article.

4.3. Simulation studies

We examined the performance of the constrained (p(s)>p(u)) and unconstrained (p(s)≠p(u)) beta-binomial mixture models via simulations. For the simulation, we used hyper-parameters estimated from a one-sided MIMOSA model fit to ICS data (univariate IL2+) from the primary immunogenicity time point. We simulated data from this constrained model with 200 subjects, a response rate of 50%, 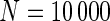, 25 000, and 50 000 cells, and 10 independent realizations of data for each 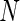. We fit the one-sided MIMOSA model to this data and evaluated the sensitivity and specificity to identify responders and non-responders through ROC analysis. MIMOSA was compared against the same methods as in Section 4.1. We repeated this procedure for the two-sided models fit to two-sided data and compared the ability of each method to properly control the FDR. For both the constrained and unconstrained simulations, MIMOSA exhibited sensitivity and specificity superior to those in competing methods, even with fewer subjects and smaller cell counts (Figures 3(A) and (C), and Figures 4(A) and 5(A) of supplementary material available at Biostatistics online). MIMOSA also provided better control of the FDR than competing approaches (Figures 3(B) and (D), and Figures 4(B) and 5(B) of supplementary material available at Biostatistics online).

Figure 3.

Comparison of positivity detection methods on data simulated from the one-sided and two-sided models. Ten simulations were generated at an 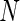of 50 000 total counts using hyper-parameter estimates from real ICS data (IFN- 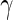expressing CD4+ T-cells stimulated with ENV-1-PTEG from HVTN065) with a 5-fold effect size between responder and non-responder components. (A) Average ROC curve over the 10 simulated data sets 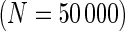, one-sided (B) Average observed and nominal FDR over 10 simulated data sets 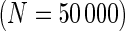, one-sided. (C) Average ROC curves, two-sided model. (D) Average observed and nominal FDR, two-sided model. Curves are shown for MIMOSA, Fisher’s exact test, the likelihood ratio test, and log fold-change. Results for MIMOSA fit to a model violating model assumptions, as well as other values of 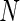(number of cells) and values of 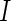(number of subjects) are in Figures 3 and 4 of supplementary material available at Biostatistics online. This figure appears in color in the electronic version of this article.

To assess the sensitivity of the model to deviations from model assumptions, we simulated data with the cell proportions drawn from truncated normal distributions with support 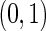, rather than beta distributions. The means and variances of the truncated normal distributions were set to the MLE of the beta distributions defined by the hyper-parameters 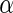and 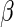estimated from the ICS data set (Figures 5(C) and (D) of supplementary material available at Biostatistics online). Even under these departures from the model assumptions, the unconstrained MIMOSA model outperformed competing methods.

5. Differential expression across biomarker combinations

Our beta-binomial model described in Section 3.1 can be generalized to a Dirichlet-multinomial model to assess differential expression across multiple biomarker combinations. As described in the data section, we now have counts for each biomarker combination, denoted by 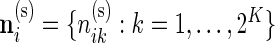and .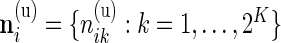

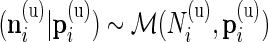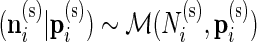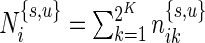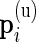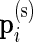In our multivariate model, the beta distribution is replaced by a multinomial distribution. Thus, the observed data are drawn from and , where are the number of cells collected and and are the unknown proportions for the unstimulated and stimulated samples, respectively.

As in the one-biomarker case, we share information across subjects using an exchangeable prior on the unknown proportions. The beta priors in Section 3.2 are replaced by Dirichlet distributions. The indicator variable 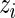is defined as in Section 3.2. As in the beta-binomial case, both EM and MCMC algorithms can be used for parameter estimation. When using a fully Bayesian approach via MCMC, we use the same priors for 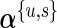and 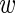as for the beta-binomial model.

We again make use of the marginal likelihoods available in closed form (see Appendix C of supplementary material available at Biostatistics online). The estimation procedures (both EM and MCMC) for the Dirichlet-multinomial are the same as for the beta-binomial model except that the number of parameters to estimate is larger. We initialize the in the EM algorithm with the positivity calls from the multivariate Fisher’s exact test. In our experience, the performance of the EM algorithm greatly deteriorates for 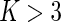, and is more dependent on the initial values and can fail to converge in many instances. Although our MCMC algorithm is slightly more computational, it does not suffer from this problem and provides a robust alternative when 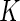is large. More details are given in Appendix C of supplementary material available at Biostatistics online.

5.1. Polyfunctionality in Fluidigm single-cell gene expression data

As a proof-of-concept, we applied our multivariate MIMOSA model to two specific genes in the Fluidigm data, namely CCR7 and GZMK. For this example, 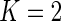and we have four possible subsets. In Figure 4, we show heatmaps of the 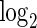counts of cells expressing all combinations of the CCR7 and GZMK genes in unstimulated and stimulated samples, as well as for the 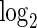of the sum of the counts of the three positive subsets. The number of CCR7GZML+ cells increases upon stimulation, while the number of CCR7+GZMK cells decreases. The typical approach to analyzing poly-functional populations from ICS data by summing the counts over all polyfunctional cell populations (i.e. cells expressing CCF7+ OR GZMK+) would not be appropriate in this case, since changes in the counts are bidirectional and their sum is near zero. The multivariate MIMOSA model tests for any difference across all polyfunctional cell subsets and detects significant differences in 12 of the 16 subjects (Figure 4(A), dark labels), whereas the standard approach detects no differences (Figure 4(B)). Testing all combinations simultaneously is also an advantage over performing multiple univariate tests on the subject combinations, which requires multiplicity adjustment and a potential loss of power.

Figure 4.

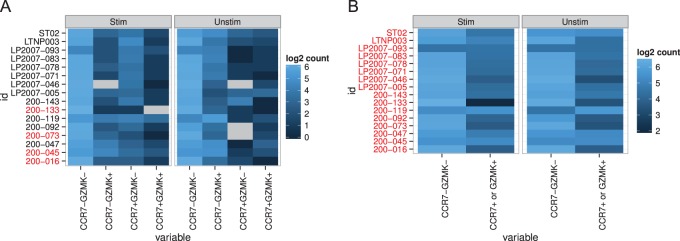
Counts of cells expressing (A) different combinations of CCR7 and GZMK genes in the unstimulated and stimulated conditions (+/+, +/, /+, /), and for (B) the marginalized positive counts in stimulated and unstimulated conditions. No difference is observed from the marginalized counts, while multivariate MIMOSA detects a difference between stimulated and unstimulated conditions in 12 of 16 samples, while Fisher’s test detects 9 of 16. Sample names highlighted in red identify those where MIMOSA did not detect a difference. This figure appears in color in the electronic version of this article.

Since the Fluidigm data set has a limited number of observations (100 cells and 16 samples), we could not look at more than two biomarkers at once. Therefore, we performed simulations in 8D to assess the performance of the multivariate MIMOSA model on the resulting 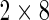tables (Figures 6(A) and (B) of supplementary material available at Biostatistics online). These results show that multivariate MIMOSA outperformed competing methods even when cell counts were small and at small effect sizes. MIMOSA also provided better FDR control than competing approaches (Figure 6(B) of supplementary material available at Biostatistics online).

6. Discussion

The development of effective statistical methods to detect differences in gene or protein expression at single-cell level is becoming increasingly important as single-cell assays become more routine and sequencing at the single-cell level eventually becomes practical (Ramsköld and others, 2012). Current approaches, such as the 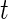-test, 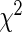test, and Fisher’s exact test, are for the most part simplistic, and resulting inference can be quite sub-optimal, especially when the cell counts are small. Most importantly, these methods do not share information across samples, resulting in less power to detect true differences than that in empirical-Bayes and hierarchical modeling approaches, which are widely applied in the microarray literature (Newton and others, 2004; Gottardo and others, 2006; Lo and Gottardo, 2007). In addition, most of these methods are univariate in nature and inappropriate for high-dimensional, next-generation single-cell assays.

The MIMOSA model uses a mixture framework to model counts in experimental subjects across multiple conditions. Information is shared across subjects through exchangeable priors, increasing the power to detect true differences compared with competing methods, even when the underlying model assumptions are violated (Figure 3 and Figure 5(B) of supplementary material available at Biostatistics online). Although in some instances the FDR was not well controlled by any method tested (Figure 1(A) of supplementary material available at Biostatistics online), volcano plots of effect size vs. posterior probability of response show that these false positives are pre-vaccine subjects exhibiting response to stimulation (Figure 7 of these false positives are pre-vaccine subjects exhibiting response to stimulation (Figure 7 of supplementary material available at Biostatistics online). Such variability is occasionally expected due to assay failures or biological variation.

MIMOSA is fit to dichotomized data (cells are positive or negative). While this is the standard approach for ICS data analysis, it is believed that the magnitude (fluorescence intensity) of the signal also carries information. For single-cell gene expression data, most methods have focused on differences in the continuous part of the signal while using the discrete on/off nature for pre-filtering (Flatz and others, 2011). The ability of MIMOSA to identify stimulation-specific expression patterns in the Fluidigm data demonstrates not only the broader utility of the method, but also that biologically relevant signal is present in the frequency of gene expression (Figure 2). We have shown elsewhere that changes in both the frequency of expression and expression level are informative (McDavid and others, 2012), and extensions of the model that incorporate the continuous component are warranted in the future. Although we used two single-cell assay platforms as motivating examples, our MIMOSA model can be applied to any type of single-cell assay where cells are dichotomized into positive and negative subsets.

Detecting differences in poly-functional cell populations is important in immunology, since it allows the identification of more homogeneous cell populations (Milush and others, 2009). In the context of HIV, poly-functional cell populations have been shown to be correlated with long-term disease non-progression, while in the context of vaccination studies poly-functional responses have been correlated with protection from disease (e.g. Betts and others, 2006; Darrah and others, 2007; Precopio and others, 2007). In the ICS data used here, the stimulation is expected to only increase the number of antigen-specific cells. The univariate MIMOSA model allows us to constrain the alternative hypothesis to the case 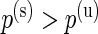, where the proportion of cells in the stimulated sample is strictly greater than the proportion of cells in the unstimulated sample, and is ideal for this situation. Hence, if a specific cell subset expressing multiple biomarkers is differentially expressed, then differential expression based on the marginal cell counts should also be detectable. As such, identifying poly-functional cytokine profiles from ICS data could be done in an iterative way. First, univariate tests on marginal populations are performed, then specific cell subsets expressing the positive biomarkers detected are tested. However, this iterative (univariate) approach might not be satisfactory due to the large number of combinations that need to be tested. A multivariate approach might be preferable. In that case, as others have pointed out, in order to have the most power to detect a true difference, the statistical test should only take into account the cytokine combinations of interest (Nason, 2006).

When changes are two-sided (as with Fluidigm), differences in poly-functional cell populations are not always detectable since differences may cancel in the marginal populations (Figure 4(B)). In this case, the use of multivariate models, as our Dirichlet-multinomial model, will be important (Figure 4(A)). Unfortunately, the limited number of samples in the Fluidigm data prevented us from looking at co-expression involving more than two genes. In the case of more than two biomarkers, the number of parameters for our model is 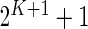, which is large even for moderate values of 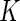. Even for 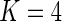, we would need a large number of subjects and cells to properly estimate the 33 parameters. A solution would be to explore alternative model parameterizations that could be used to reduce the number of required parameters. For example, one could assume that the hyper-parameters are constant across biomarker combinations, that is, 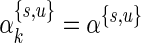for all 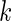, and the number of parameters would be reduced to 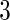for any 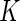. In reality, such a model would be unrealistic, given that certain stimulations are known to induce expression of certain biomarkers more than others. More exploratory work will need to be done in this area once high-dimensional single-cell level data with large number of samples become available.

The results presented here were obtained with an R and C++ implementation the MIMOSA model, freely available at http://www.github.org/RGLab/MIMOSA. The code to replicate the analysis is available at http://www.github.org/RGLab/MIMOSA_manuscript/MIMOSA/mimosafigures.

Supplementary material

Supplementary Material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the Intramural Research Program of the National Institute of Allergy and Infectious Diseases (NIAID) and the National Institutes of Health (NIH) grants [R01 EB008400, U01 AI068635-01], the Bill and Melinda Gates Foundation through grants to the Vaccine and Immunology Statistical Center (VISC) [OPP38744, OPP1032317], and the Collaboration for AIDS Vaccine Discovery (CAVD) [OPP1032325]. HVTN065 was conducted by the HIV Vaccine Trials Network (HVTN) and supported by NIAID. The HVTN Lab Program is supported by the NIH [UM1AI068618], the Public Health Service, and the University of Washington Center for AIDS Research [UM1 AI068618, P30 AI027757]. This work was performed as a project of the Human Immune Phenotyping Consortium (HIPC) and funded by the NIAID [U19AI089986].

Supplementary Material

Supplementary Data

Acknowledgements

Thanks to the James B. Pendleton Charitable Trust for a generous equipment donation. Conflict of Interest: None declared.

References

1. Altman J. D., Moss P. A., Goulder P. J., Barouch D. H., McHeyzer-Williams M. G., Bell J. I., McMichael A. J., Davis M. M. Phenotypic analysis of antigen-specific T lymphocytes. Science (New York, NY) 1996;274:5284. doi: 10.1126/science.274.5284.94. [DOI] [PubMed] [Google Scholar]
2. Benjamini Y., Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995;57(1):289–300. [Google Scholar]
3. Betts M. R., Nason M. C., West S. M., De Rosa S. C., Migueles S. A., Abraham J., Lederman M. M., Benito J. M., Goepfert P. A., Connors M. and others. Hiv nonprogressors preferentially maintain highly functional hiv-specific cd8+ t cells. Blood. 2006;107(12):4781–4789. doi: 10.1182/blood-2005-12-4818. [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Darrah P. A., Patel D. T., De Luca P. M., Lindsay R. W. B., Davey D. F., Flynn B. J., Hoff S. T., Andersen P., Reed S. G., Morris S. L. and others. Multifunctional TH1 cells define a correlate of vaccine-mediated protection against Leishmania major. Nature Medicine. 2007;13(7):843–850. doi: 10.1038/nm1592. [DOI] [PubMed] [Google Scholar]
5. De Rosa S. C., Lu F. X., Yu J., Perfetto S. P., Falloon J., Moser S., Evans T. G., Koup R., Miller C. J., Roederer M. Vaccination in humans generates broad t cell cytokine responses. Journal of Immunology. 2004;173(9):5372–5380. doi: 10.4049/jimmunol.173.9.5372. [DOI] [PubMed] [Google Scholar]
6. Dempster A. P., Laird N. M., Rubin D. B. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 1977;39(1):1–38. [Google Scholar]
7. Flatz L., Roychoudhuri R., Honda M., Filali-Mouhim A., Goulet J.-P., Kettaf N., Lin M., Roederer M., Haddad E. K., Sékaly R. P. and others. Single-cell gene-expression profiling reveals qualitatively distinct CD8 T cells elicited by different gene-based vaccines. Proceedings of the National Academy of Sciences. 2011;108:5724–5729. doi: 10.1073/pnas.1013084108. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Gelfand A. E., Smith A. F. M. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85(410):398–409. [Google Scholar]
9. Goepfert P. A., Elizaga M. L., Sato A., Qin L., Cardinali M., Hay C. M., Hural J., DeRosa S. C., DeFawe O. D., Tomaras G. D. and others. Phase 1 safety and immunogenicity testing of DNA and recombinant modified vaccinia ankara vaccines expressing HIV-1 virus-like particles. Journal of Infectious Diseases. 2011;203(5):610–619. doi: 10.1093/infdis/jiq105. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Gottardo R., Raftery A. E., Ka Yee Y., Bumgarner R. Bayesian robust inference for differential gene expression in microarrays with multiple samples. Biometrics. 2006;62:10–18. doi: 10.1111/j.1541-0420.2005.00397.x. [DOI] [PubMed] [Google Scholar]
11. Horton H., Thomas E. P., Stucky J. A., Frank I., Moodie Z., Huang Y., Chiu Y. L., McElrath M. J., De Rosa S. C. Optimization and validation of an 8-color intracellular cytokine staining (ICS) assay to quantify antigen-specific t cells induced by vaccination. Journal of Immunological Methods. 2007;323(1):39–54. doi: 10.1016/j.jim.2007.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Ihaka R., Gentleman R. R: A language for data analysis and graphics. Journal of Computational and Graphical Statistics. 1996;5(3):299–314. [Google Scholar]
13. Inokuma M., dela Rosa C., Schmitt C., Haaland P., Siebert J., Petry D., Tang M., Suni M. A., Ghanekar S. A., Gladding D. and others. Functional T cell responses to tumor antigens in breast cancer patients have a distinct phenotype and cytokine signature. Journal of Immunology. 2007;179(4):2627–2633. doi: 10.4049/jimmunol.179.4.2627. [DOI] [PubMed] [Google Scholar]
14. Lo K., Gottardo R. Flexible empirical Bayes models for differential gene expression. Bioinformatics. 2007;23(3):328–335. doi: 10.1093/bioinformatics/btl612. [DOI] [PubMed] [Google Scholar]
15. McDavid A., Finak G., Chattopadyay P. K., Dominguez M., Lamoreaux L., Ma S. S., Roederer M., Gottardo R. Data exploration, quality control and testing in single-cell qPCR-based gene expression experiments. Bioinformatics. 2012;29(4):9. doi: 10.1093/bioinformatics/bts714. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. McKinstry K. K., Strutt T. M., Swain S. L. The potential of CD4 T-cell memory. Immunology. 2010;130(1):1–9. doi: 10.1111/j.1365-2567.2010.03259.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Milush J. M., Long B. R., Snyder-Cappione J. E., Cappione A. J., York V. A., Ndhlovu L. C., Lanier L. L., Michaëlsson J., Nixon D. F. Functionally distinct subsets of human NK cells and monocyte/DC-like cells identified by coexpression of CD56, CD7, and CD4. Blood. 2009;114(23):4823–4831. doi: 10.1182/blood-2009-04-216374. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Nason M. Patterns of immune response to a vaccine or virus as measured by intracellular cytokine staining in flow cytometry: hypothesis generation and comparison of groups. Journal of Biopharmaceutical Statistics. 2006;16(4):483–498. doi: 10.1080/10543400600719426. [DOI] [PubMed] [Google Scholar]
19. Newton M. A., Noueiry A., Sarkar D., Ahlquist P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics (Oxford, England) 2004;5(2):155–176. doi: 10.1093/biostatistics/5.2.155. [DOI] [PubMed] [Google Scholar]
20. Peiperl L., Morgan C., Moodie Z., Li H., Russell N., Graham B. S., Tomaras G. D., De Rosa S. C., McElrath M. J. and The NIAID HIV Vaccine Trials Network. Safety and immunogenicity of a replication-defective adenovirus type 5 hiv vaccine in ad5-seronegative persons: a randomized clinical trial (hvtn 054) PLoS ONE. 2010;5(10):13579. doi: 10.1371/journal.pone.0013579. [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Precopio M. L., Betts M. R., Parrino J., Price D. A., Gostick E., Ambrozak D. R., Asher T. E., Douek D. C., Harari A., Pantaleo G. and others. Immunization with vaccinia virus induces polyfunctional and phenotypically distinctive CD8(+) T cell responses. The Journal of Experimental Medicine. 2007;204(6):1405–1416. doi: 10.1084/jem.20062363. [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Proschan M. A., Nason M. Conditioning in 2 × 2 tables. Biometrics. 2009;65(1):316–322. doi: 10.1111/j.1541-0420.2008.01053.x. [DOI] [PubMed] [Google Scholar]
23. Ramsköld D., Luo S., Wang Y.-C., Li R., Deng Q., Faridani O. R., Daniels G. A., Khrebtukova I., Loring J. F., Laurent L. C. and others. Full-length mRNA-Seq from single-cell levels of RNA and individual circulating tumor cells. Nature Biotechnology. 2012;30:777–782. doi: 10.1038/nbt.2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Sinclair E., Black D., Epling C. L., Carvidi A., Josefowicz S. Z., Bredt B. M., Jacobson M. A. CMV antigen-specific CD4+ and CD8+ T cell IFNgamma expression and proliferation responses in healthy CMV-seropositive individuals. Viral Immunology. 2004;17(3):445–454. doi: 10.1089/0882824041857049. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Trigona W. L., Clair J. H., Persaud N., Punt K., Bachinsky M., Sadasivan-Nair U., Dubey S., Tussey L., Fu T.-M., Shiver J. Intracellular staining for HIV-specific IFN-gamma production: statistical analyses establish reproducibility and criteria for distinguishing positive responses. Journal of Interferon & Cytokine Research: The Official Journal of the International Society for Interferon and Cytokine Research. 2003;23(7):369–377. doi: 10.1089/107999003322226023. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data