CFTR Gating II: Effects of Nucleotide Binding on the Stability of Open States (original) (raw)
Abstract
Previously, we demonstrated that ADP inhibits cystic fibrosis transmembrane conductance regulator (CFTR) opening by competing with ATP for a binding site presumably in the COOH-terminal nucleotide binding domain (NBD2). We also found that the open time of the channel is shortened in the presence of ADP. To further study this effect of ADP on the open state, we have used two CFTR mutants (D1370N and E1371S); both have longer open times because of impaired ATP hydrolysis at NBD2. Single-channel kinetic analysis of ΔR/D1370N-CFTR shows unequivocally that the open time of this mutant channel is decreased by ADP. ΔR/E1371S-CFTR channels can be locked open by millimolar ATP with a time constant of ∼100 s, estimated from current relaxation upon nucleotide removal. ADP induces a shorter locked-open state, suggesting that binding of ADP at a second site decreases the locked-open time. To test the functional consequence of the occupancy of this second nucleotide binding site, we changed the [ATP] and performed similar relaxation analysis for E1371S-CFTR channels. Two locked-open time constants can be discerned and the relative distribution of each component is altered by changing [ATP] so that increasing [ATP] shifts the relative distribution to the longer locked-open state. Single-channel kinetic analysis for ΔR/E1371S-CFTR confirms an [ATP]-dependent shift of the distribution of two locked-open time constants. These results support the idea that occupancy of a second ATP binding site stabilizes the locked-open state. This binding site likely resides in the NH2-terminal nucleotide binding domain (NBD1) because introducing the K464A mutation, which decreases ATP binding affinity at NBD1, into E1371S-CFTR shortens the relaxation time constant. These results suggest that the binding energy of nucleotide at NBD1 contributes to the overall energetics of the open channel conformation.
Keywords: chloride channel, single-channel kinetics, ABC transporter, energetics, macroscopic relaxation
INTRODUCTION
The cystic fibrosis transmembrane conductance regulator (CFTR) is a chloride channel that belongs to the ATP-binding cassette (ABC) transporter family. PKA-dependent phosphorylation of CFTR is a prerequisite for the opening and closing (gating) of the channel by ATP binding/hydrolysis (for review see Gadsby and Nairn, 1999). CFTR contains two nucleotide binding domains (NBD1 and NBD2) with consensus sequences for ATP binding and/or hydrolysis. Not surprisingly, these two domains have been proposed to be the sites upon which ATP acts to open and close the channel gate. However, the detailed molecular mechanism of ATP-dependent gating is unclear.
Recently the crystal structures of several NBDs from different prokaryocyte members of the ABC family have been solved (Hung et al., 1998; Diederichs et al., 2000; Gaudet and Wiley, 2001; Karpowich et al., 2001; Yuan et al., 2001; Smith et al., 2002; Schmitt et al., 2003; Verdon et al., 2003). There is growing evidence that the NBDs form a dimeric structure with the two ATP-binding sites buried in the dimer interface (Smith et al., 2002; Chen et al., 2003). Hopfner et al. (2000) suggested that ATP binding drives the NBD dimerization of the distantly related DNA repair protein Rad50, based on biochemical and structural data. This ATP-driven dimerization of the NBDs was confirmed in bacterial ABC transporters by Moody et al. (2002). They showed that MJ0796 and MJ1267, two bacterial ABC transporters' NBDs, can form homodimers in the presence of ATP, when hydrolysis was prevented through the mutation of the Walker B glutamate. Moreover, neither ADP nor AMP-PNP promoted stable dimerization, suggesting that a hydrolyzable gamma phosphate is required for a stable dimer formation. Since dimers were not observed in wild-type (WT) NBDs in the presence of ATP, it was speculated that the free energy from ATP hydrolysis results in dissociation of the WT dimer (Moody et al., 2002; Smith et al., 2002).
Lewis et al. (2004) crystallized the NBD1 from mouse CFTR, and found that the structure is very similar to that of NBDs from bacterial ABC transporters, in spite of limited sequence identity. It is interesting to note that purified NBD1 of the mouse CFTR does not hydrolyze ATP presumably because of a lack of Walker B glutamate at NBD1 (Lewis et al., 2004). Although it is unknown whether CFTR's two NBDs form a heterodimer, it has been hypothesized that ATP binding at both NBDs drives the dimerization reaction, which leads to channel opening, and that ATP hydrolysis at NBD2 breaks the dimer and consequently closes the channel (Vergani et al., 2003).
Several models have been proposed in the past to explain the gating mechanism of CFTR channels. Although the detailed mechanism of CFTR gating by its two NBDs remains controversial, there is some agreement regarding how ATP binding at the NBDs leads to opening and closing of the channel. Since the mutation of the Walker A lysine K1250 in NBD2, which abolishes hydrolysis, results in channels with prolonged burst durations, it was proposed that hydrolysis at NBD2 leads to channel closing (Carson et al., 1995; Gunderson and Kopito, 1995; Zeltwanger et al., 1999; cf. Aleksandrov and Riordan, 1998; Aleksandrov et al., 2000). However, the mechanism for channel opening remains unsettled. Previous studies suggested that ATP hydrolysis at NBD1 was involved in the opening of the channel since mutations of the Walker A lysine at NBD1 (e.g., K464A) decrease the channel opening rate (Carson et al., 1995; Gunderson and Kopito, 1995; cf. Zeltwanger et al., 1999). However, Powe et al. (2002) reexamined the gating kinetics of K464A mutant CFTR and found little difference in the opening rate between this mutant and WT-CFTR. In addition, biochemical studies demonstrate an occlusion of ATP in NBD1 (Szabo et al., 1999; Basso et al., 2003), suggesting that association–dissociation of ATP from NBD1 is too slow to account for the opening and closing transitions observed in electrophysiological experiments. It is therefore unclear what role NBD1 is playing in CFTR gating.
A clue to the role of NBD1 was the finding by Vergani et al. (2003) of a rightward shift of the ATP dose response when either one of the two Walker A lysines (K464 or K1250) is altered to alanine. A similar observation was made for the mutation at the Walker B aspartate at NBD2 (D1370). Based on these observations, they proposed a model for CFTR gating in which ATP binding at both NBDs is a requirement for channel opening, and hydrolysis at NBD2 leads to channel closing (i.e., Scheme 2 in the accompanying paper). This latest gating scheme can explain the competitive inhibition of ADP for channel opening. However, it is not immediately clear how the model would explain a decrease of channel opening time by ADP (see accompanying paper for details).
To study in more detail the effect of nucleotide binding on the open time of CFTR, we used both macroscopic current relaxation and single-channel kinetic analysis for CFTR mutants with impaired ATP hydrolysis: specifically, the D1370N and E1371S mutations in NBD2. The D1370 residue coordinates Mg2+, a cofactor for ATP hydrolysis. Mutation of this aspartate to asparagine (D1370N) results in channels that exhibit longer open and closed times (Gunderson and Kopito, 1995; Vergani et al., 2003), resembling the elusive “slow gating” mode described in our previous paper (Bompadre et al., 2005). The E1371 residue serves as a catalytic base for ATP hydrolysis. Mutation of this glutamate to serine produces a channel (E1371S) that presents long “locked-open” times (Aleksandrov et al., 2000; Vergani et al., 2003). These hydrolysis-impaired mutations were also studied in the ΔR background, which allows single-channel kinetic analysis in the absence of dephosphorylation-induced rundown of channel activity.
Single-channel dwell-time analysis of ΔR/D1370N-CFTR channels shows unequivocally that the open time of the channel is decreased in the presence of ADP. Relaxation analysis of macroscopic ΔR/E1371S-CFTR currents upon nucleotide removal shows two different relaxation time constants in the presence of ADP and ATP, indicating that ADP induces a different locked-open state. Moreover, studies of ΔR/E1371S-CFTR open time in patches containing a single channel at three different ATP concentrations show a change of the relative frequency of the different open times, suggesting the presence of an ATP-binding site, occupancy of which affects the stability of the open state. Similar results were obtained in E1371S mutants constructed in the WT background. Kinetic and structural implications of our results are discussed.
MATERIALS AND METHODS
Construction of CFTR Mutants
CFTR mutations E1371S and D1370N were introduced into the plasmid pBQ4.7 WT-CFTR (Powe et al., 2002) by using the QuikChange kit (Stratagene). The 0.9-kb PflMI-XhoI fragments containing the mutations from the pBQ4.7 were used to substitute the corresponding regions in pBudCE4.1 split ΔR CFTR (Ai et al., 2004) to obtain pBudCE4.1 ΔR/D1370N and pBudCE4.1 ΔR/E1371S CFTR. Similarly, the 0.9-kb PflMI-EcoRV fragments were used to replace the corresponding ones in pcDNA 3.1 WT-CFTR or pcDNA 3.1 K464A-CFTR (Powe et al., 2002) to generate pcDNA3.1 D1370N, pcDNA 3.1 E1371S, and pcDNA3.1 K464A/E1371S CFTR constructs. All constructs were sequenced to ensure the presence of mutations (DNA core, University of Missouri).
Cell Culture and Transient Expression of CFTR
Chinese hamster ovary (CHO) cells were grown and transfected with the above-mentioned CFTR mutants as previously described (Bompadre et al., 2005).
Reagents
Mg-ATP purchased from Sigma-Aldrich, was stored in water at −20°C. PKA was purchased from Promega. ADP was purchased from Calbiochem and stored in water at −20°C.
Single-channel Experiments
Single-channel experiments were as described in Bompadre et al. (2005).
Data Analysis
Single-channel dwell-time analysis is described in Bompadre et al. (2005). Fitting of the time course of current relaxation upon removal of nucleotides with single or double exponentials was performed with Igor. For dwell-time analysis of ΔR/E1371S-CFTR data, we pooled the current records obtained from several patches containing only one channel. No cutoff was used for the construction of the closed time histograms and therefore the histogram is constrained by the bandwidth of the recording. The open time histograms were reconstructed by setting a cutoff time of 500 ms to exclude the ATP-independent closings (see results for details). The resulting open time histograms show at least two locked-open states (see Fig. 6). To quantify the kinetic parameters within the locked-open events, we used 50 s as a cutoff to separate short-lived and long-lived locked-open events. Least square estimation with sums of exponential components was performed to obtain open and closed time constants. Events shorter than dead times were excluded from the fitting.
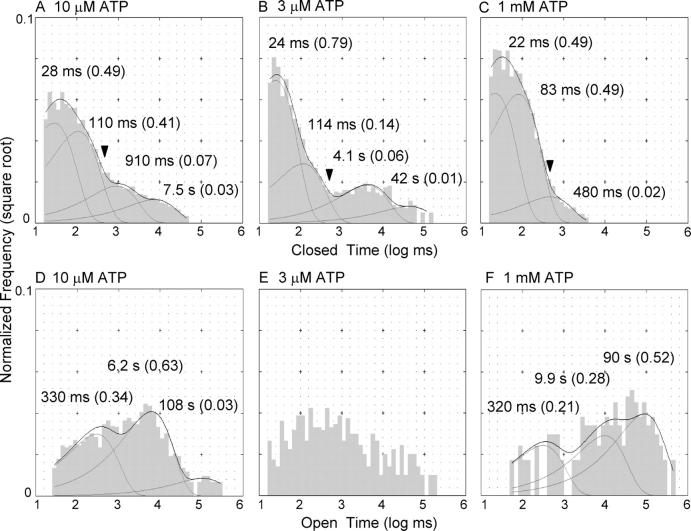
Figure 6.
Single-channel dwell time analysis of ΔR/E1371S-CFTR. (A) Events from two single-channel recordings (∼50 min each) were pooled together to construct this closed time histogram. The closed time distribution for data obtained at 10 μM ATP can be fitted with a quadruple exponential function. No cutoff was used for the construction of this histogram. The arrow marks the cutoff (500 ms) used to define the minimum of the ATP-dependent closed times used for the open time analysis in D. (B) The closed time distribution for data obtained at 3 μM ATP and fitting parameters. (C) Events from two recordings of single channels in the presence of 1 mM ATP were pooled together to construct this closed time histogram (∼100 min of recording). The closed time distribution can be fitted with a triple exponential function. No cutoff was used for the construction of this histogram. The arrow marks the cutoff used to construct the open time histogram shown in F. (D) The open time histogram for data obtained at 10 μM ATP shows the presence of three distinct burst lengths: a brief opening of 330 ms, an intermediate burst of 6 s (most of the events), and very few lock-open bursts with a time constant of ∼100 s. (E) The open time histogram for the recording at 3 μM ATP. (F) The open time histogram shows that most of the events are long-lived locked-open bursts (>50%).
Kinetics of spontaneous openings in the absence of ATP was assessed manually with Igor. Since the spontaneous opening rate is extremely low, only single-channel openings were seen, even though most of the patches contained multiple channels. Therefore, the measured open times are fairly accurate. Since the number of events was very small, the lengths of the openings measured in different patches were pooled together and a survivor plot was constructed as in Zeltwanger et al. (1999). The data was fitted with an exponential function using Igor. To calculate the opening rate, the closed time before each opening was also measured manually using Igor, and the average opening rate (reciprocal of the averaged closed time) was calculated. Then, to calculate the spontaneous opening rate per channel, we divided the calculated opening rate by the number of channels in the patch.
Online Supplemental Material
The online supplemental material for this paper consists of one figure (available at http://www.jgp.org/cgi/content/full/jgp.200409228/DC1). Fig. S1 shows the ATP dose response for the D1370N mutant.
RESULTS
Effect of ADP on ΔR/D1370N-CFTR
In the accompanying paper (Bompadre et al., 2005), we demonstrated that ADP can shorten the open time of ΔR-CFTR and this effect is more prominent when the channel is in the slow gating mode with longer open times. Since the D1370N mutants exhibit open and closed times on the order of seconds (i.e., they mimic the slow gating mode described in Bompadre et al., 2005), we decided to use this mutant to further study the effect of ADP on the open time. Vergani et al. (2003) found that the ATP dose response for the D1370N mutant shifted to the right compared with that of WT channel. We first examined the ATP dose–response relationship for this mutant in the WT background, and found little difference with the ATP dose response for WT channels (Fig. S1, available at http://www.jgp.org/cgi/content/full/jgp.200409228/DC1).
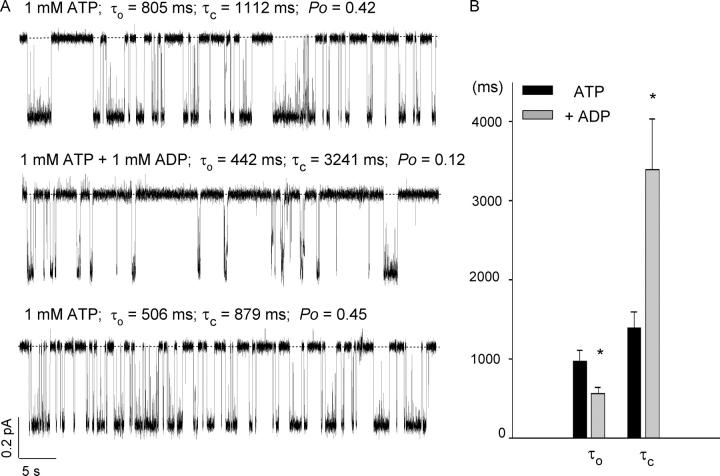
To study the effect of ADP on single-channel kinetics, we introduced the D1370N mutation into the ΔR-CFTR background because ΔR-CFTR is insensitive to dephosphorylation-induced rundown, and we can more easily obtain patches with fewer channels for kinetic analysis (Bompadre et al., 2005). In excised inside-out patches, ΔR/D1370N-CFTR channels were opened with 1 mM ATP, and subsequent application of 1 mM ATP plus 1 mM ADP inhibited the currents by an average of 63 ± 5% (n = 5). Bracketing ADP experiments with 1 mM ATP controls ensured us that little rundown was present (Fig. 1 A). Kinetic analysis for patches containing up to four channels was performed as described (see materials and methods). As expected, the mean closed time increases from 1387 ± 201 ms to 3383 ± 645 ms in the presence of ADP. In all five patches, the open time constant is decreased significantly (P < 0.01). This decrease of the open time is readily apparent for patches containing only one channel as shown in Fig. 1 A. The average decrease of the open time constant was 43 ± 11%, from 976 ± 126 to 558 ± 84 ms (Fig. 1 B). These results confirm that ADP does indeed shorten the channel open time. Although we speculate that this decrease of the open time is caused by the presence of another open state when ADP, not ATP, is bound (see discussion for details), the model used (Scheme 1 in Bompadre et al., 2005) for data analysis does not allow us to separate two different open states. Furthermore, the open time constant for D1370N-CFTR may still be too short for isolating the putative ADP-bound open state. We therefore constructed another mutant, E1371S, which has an open time on the order of tens or hundreds of seconds because the ATP hydrolysis is abolished at NBD2 (Aleksandrov et al., 2000; Vergani et al., 2003).
Figure 1.
ADP shortens the open time of ΔR/D1370N-CFTR channels. (A) Single-channel current traces in the presence of 1 mM ATP, 1 mM ATP + 1 mM ADP, or 1 mM ATP again. (B) Effects of ADP on the mean open and closed times. Notice that ADP shortens the mean open time and increases the mean closed time (n = 5). Error bars represent SEM. * indicates P < 0.01.
ADP Effect on ΔR/E1371S Mutant
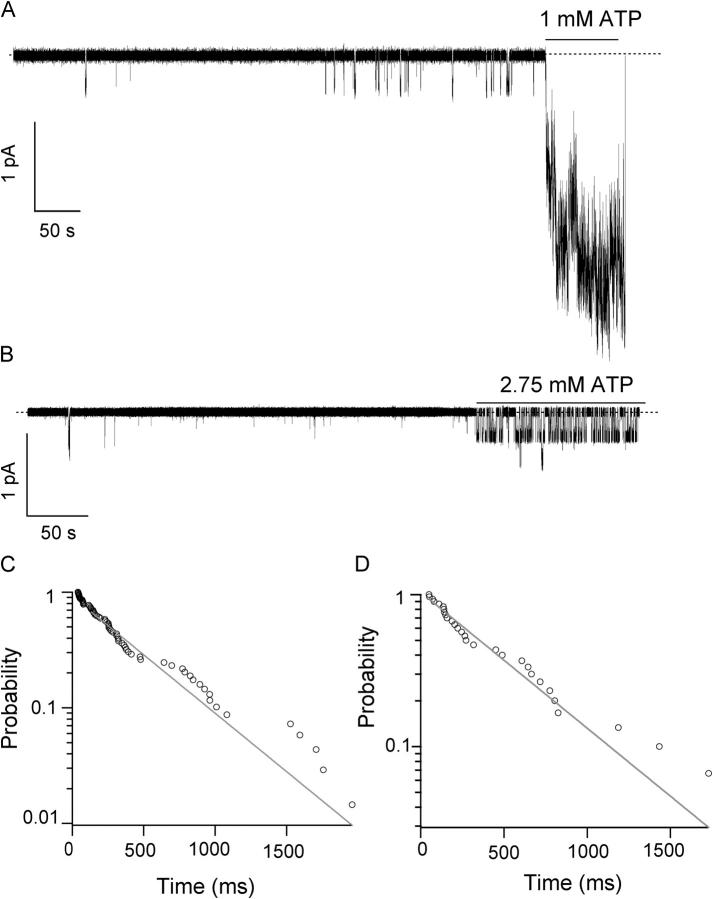
We first introduced the E1371S mutation into the ΔR background in order to study the behavior of this channel in the presence or absence of ADP without having to worry about the possible effect of dephosphorylation on the channel open time. Fig. 2 A shows a representative experiment in an excised inside-out patch. In the presence of 1 mM ATP, the steady-state macroscopic current shows very fast fluctuations resulting from brief flickery closures. But, the overall fluctuation is fairly small relative to the macroscopic mean current amplitude, indicating that the Po is close to unity (also see below). When the nucleotide was washed out, one can follow the slow closing of each channel (in this case, the number of steps is 10).
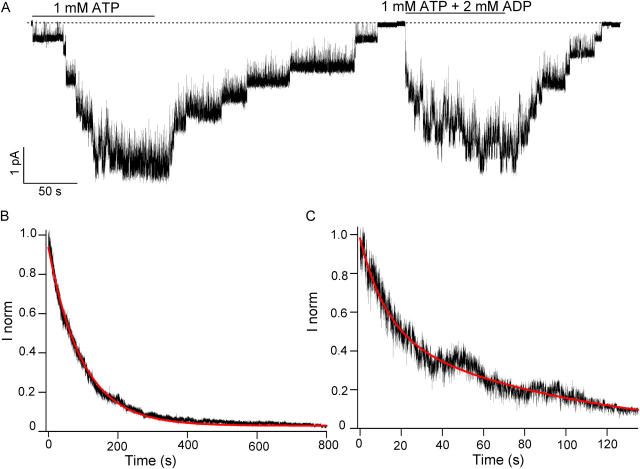
Figure 2.
Macroscopic current relaxation for ΔR/E1371S-CFTR channels in the presence of ATP and ADP. (A) A sample trace of current relaxations for ΔR/E1371S-CFTR channels opened with 1 mM ATP, and subsequently with 1 mM ATP + 2 mM ADP. (B) The current decay upon removal of ATP can be fitted with a single exponential function with a time constant of 100.00 ± 0.02 s. (C) The current decay upon removal of ATP plus ADP is fitted with a double exponential function with time constants of 12.9 ± 0.1 and 105 ± 3 s.
Once all channels are closed, subsequent application of 1 mM ATP plus 2 mM ADP elicits a smaller current with clearly different current fluctuations. Unlike the trace in the presence of ATP alone, all 10 channels seldom open at the same time. Compared with the relaxation time course with ATP alone, the current relaxation of ΔR/E1371S-CFTR channels opened by ATP plus ADP is faster. We pooled relaxations from 47 different patches with channels opened by 1 mM ATP to generate an ensemble macroscopic current. The relaxation time course can be fitted with a single exponential function with a relaxation time constant (representing the locked open time) of 100.00 ± 0.02 s (Fig. 2 B). We cannot rule out the possibility of a better fit with a higher order of exponential function since the fitted curve does not cover well the very beginning of the current decay. Similar relaxation analysis done on the ensemble current from 17 different patches exposed to ATP plus ADP shows a double exponential decay with relaxation time constants of 12.9 ± 0.1 (46%) and 105 ± 3 s (54%) (Fig. 2 C). It should be noted that the longer time constant is similar to the one obtained for the current relaxation upon removal of 1 mM ATP. These data can be explained if ADP induces another locked-open state with a shorter time constant. This result constitutes the first piece of evidence that two different locked-open states are present in the presence of ATP and ADP. The presence of two populations of channels, one with a very long locked-open time and one with a shorter one, suggests that for some channels ATP has been replaced by ADP at a nucleotide binding site, yielding a less stable locked-open state. Since binding of ADP at one nucleotide binding site competitively prevents ATP from opening the channel (shown in the accompanying paper), this effect of ADP on the locked-open time likely reflects competitive binding of ADP at a different binding site.
ATP Concentration Dependence of ΔR/E1371S Current Relaxation
Our experiments with ADP suggest the presence of a nucleotide binding site, occupancy of which by ATP or ADP can affect the stability of the locked-open state. Based on this idea, one will predict that lowering [ATP] alone could affect the probability of occupancy of this binding site that affects the channel's locked-open time. If ADP, instead of ATP, binding at this site affects the relaxation, a lack of ATP binding (i.e., unoccupied binding site) may also affect the locked-open time constant. We thus performed similar relaxation experiments using a lower ATP concentration.
Fig. 3 A shows a representative relaxation experiments for ΔR/E1371S-CFTR channels opened with 10 μM ATP. Like the macroscopic current in the presence of ATP plus ADP, the macroscopic current induced by 10 μM ATP exhibits much larger fluctuations. Upon nucleotide removal, the current decay is fast at first and then becomes slower, indicating the presence of multiple exponential components reflecting different populations of locked-open states. Ensemble current was generated by pooling data from 22 different patches (Fig. 3 B). The relaxation curve shows a very fast component at the beginning of the washout (Fig. 3 B, inset), then the major relaxation takes place within the first 30 s (a time much shorter than the relaxation time constant for 1 mM ATP), and a final tail that can last for several minutes The current relaxation at 1 mM ATP (from Fig. 2 B) is plotted for comparison (Fig. 3 B, dash line). Unfortunately our solution change is not fast enough to resolve well the fastest component, and the longest component apparently only takes a minor fraction of the total current decay, thus we cannot do a multiple exponential fit to the relaxation time course. Nevertheless, since the relaxation experiments were performed by completely removing ATP, the channels, once opened by ATP, can only close without the possibility of reopening by ATP again. Three different relaxation time courses must reflect three different ATP-induced open states. Even without quantitative curve fitting, a faster current decay upon removal of 10 μM ATP, compared with that with 1 mM ATP, corroborate with the idea of the presence of an ATP binding site, occupancy of which stabilizes the locked-open state.
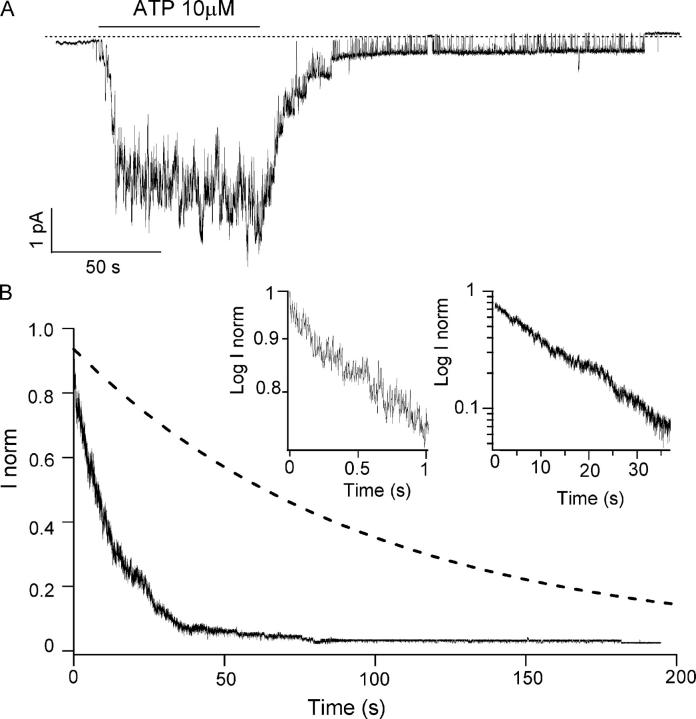
Figure 3.
Macroscopic current relaxation for ΔR/E1371S-CFTR opened with 10 μM ATP. ΔR/E1371S-CFTR channels were activated with 10 μM ATP until the current reached a steady state. Then the nucleotide was washed out. (A) Sample trace. (B) Ensemble currents were generated by pooling data from 22 experiments. The insets show the first two components of the current relaxation. The dash line represents current relaxation of ΔR/E1371S-CFTR upon removal of 1 mM ATP (from Fig. 2 B).
Single-channel Analysis of ΔR/ E1371S Mutant
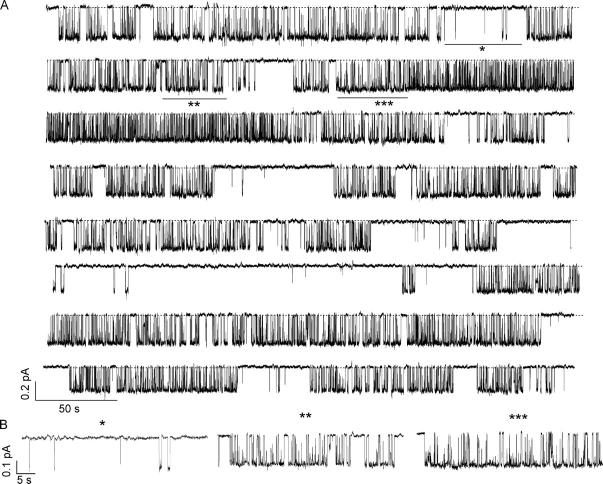
Fig. 4 shows a continuous recording of a single ΔR/E1371S mutant channel in the presence of 1 mM ATP that lasts for ∼50 min. It is apparent that the channel remains locked open for minutes, with a Po close to unity. Close inspection of the recording reveals that, like WT-CFTR, this mutant channel occasionally sojourns into various subconductance states (Tao et al., 1996; Wang et al., 1998). While most of the closings represent flickery closures, some closed events last for hundreds of milliseconds to seconds. Some of these long-lasting closures likely represent ATP-dependent closed time (τc = ∼500 ms for ΔR-CFTR at 1 mM ATP; Bompadre et al., 2005).
Figure 4.

Single-channel recording of ΔR/E1371S-CFTR in the presence of 1 μM ATP. A continuous, 54-min single-channel trace in the presence of 1 mM ATP. Note that the channel is open most of the time. The Po is almost 1.
The same experiment was done with a single channel in the presence of 10 μM ATP, and the result is remarkably different (Fig. 5). Closed events that last for several seconds can be easily discerned by eye. These long closed events are expected because of a lower opening rate of the channel at low [ATP] (τc = ∼3.7 s for ΔR-CFTR at 10 μM ATP; Bompadre et al., 2005). These long closed events also allow us to clearly distinguish opening bursts of different lengths. Consistent with the macroscopic relaxation (Fig. 3), at least three different opening bursts can be distinguished by eye inspection. There are many brief openings that last for tens or hundreds of milliseconds (marked *). One rarely sees an extremely long opening burst lasting for several minutes (marked ***). Most of the opening bursts are on the order of a few seconds (marked **; Fig. 5 B).
Figure 5.
Single-channel recording of ΔR/E1371S-CFTR in the presence of 10 μM ATP. (A) A continuous 45-min single-channel trace in the presence of 10 μM ATP. Note that the channel remains closed for long periods, and presents opening bursts of different lengths. (B) Expanded traces of selected parts of the trace in A. Note the presence of very brief openings (*), and intermediate locked-open events (**), and rarely occurring long locked-open events (***).
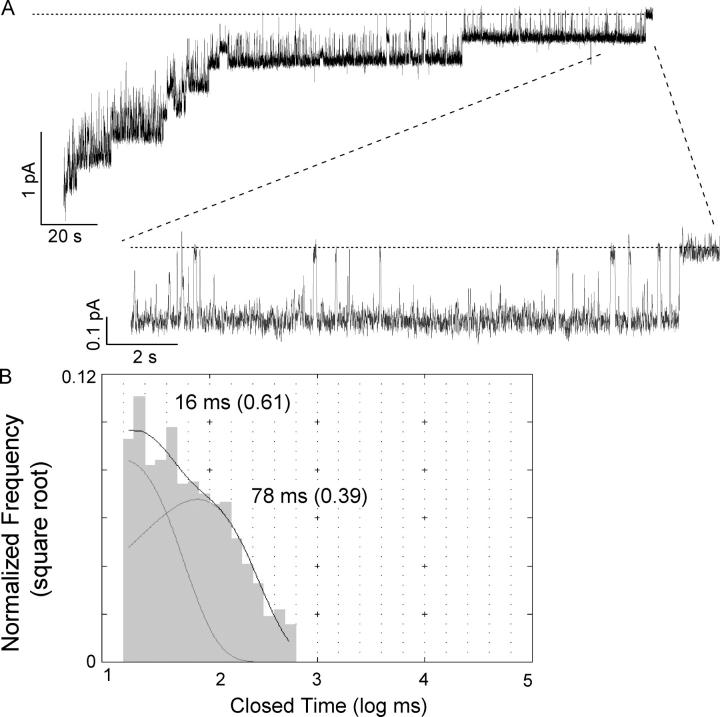
We pooled data from two recordings (∼50 min long each) at 10 μM ATP concentration and analyzed the single-channel dwell time distributions. The closed time histogram shows the presence of four components: a brief closing (flickers), a slightly longer closed event (∼110 ms), and two longer closed time constants of 910 ms and 7.5 s (Fig. 6 A). We also analyzed one long recording (∼80 min) of ΔR/E1371S-CFTR at 3 μM ATP (Fig. 6 B). Compared with the histogram in Fig. 6 A, this closed time distribution shows major differences in those long closed events. One can even observe events that last >100 s. This wide distribution of closed time over four orders of magnitude in length further supports the presence of multiple closed states. We fitted the closed time histogram with a quadruple exponential function. By comparing these two histograms at two ATP concentrations, we tentatively conclude that among these four closed time constants, those two short ones are ATP independent, whereas the long ones are ATP dependent (also see Fig. 6 C).
If assigning the long closed time constants as ATP dependent is correct, by isolating these ATP-dependent closed events with the use of a proper cutoff value, one should be able to reproduce the three types of opening bursts revealed by macroscopic relaxation analysis (Fig. 3 B). We chose 500 ms as the cutoff value since it is at the nadir of those two distributions for intermediate and long closed times (Fig. 6 A, arrowhead). The resulting open time histogram can be fitted with a triple exponential function, yielding the open time constants of 330 ms, 6.2 s, and 108 s (Fig. 6 D). The open time histogram for the recording at 3 μM ATP was not further analyzed because no corresponding macroscopic relaxation experiments were performed for comparison (Fig. 6 E). Nevertheless, compared with the histogram shown in Fig. 6 D, the open time distribution at 3 μM ATP in general is shifted to the left, indicating a predominance of shorter events. The values of these three open time constants obtained at 10 μM ATP correspond well with the three relaxation time courses shown in Fig. 3 B. The relative proportion of these three components (97% of the events belong to the two shorter openings and 3% for the long lasting events) also reasonably fits the results predicted from the macroscopic relaxation analysis. We thus conclude that at 10 μM ATP, there are at least three open states (a brief open state, OB, a short locked-open state, LOS, and a long locked-open state, LOL).
We then analyzed the 1 mM ATP data in the same way. Even with an overall recording of ∼100 min in duration, the closed time histogram was dominated by short closed events with very few long closings. Nevertheless, the histogram can be better fitted with a triple exponential function. In addition to the very brief flickery closings, we also observe intermediate closed events with a time constant close to 100 ms, and a longer closed time of ∼500 ms (Fig. 6 C). Compared with the closed time histograms from recordings with 10 μM (Fig. 6 A) or 3 μM ATP (Fig. 6 B), it appears that the two shorter closed time constants remain little affected with an increase of [ATP], again supporting the notion that these two short-lived closed states are ATP independent.
It is very difficult to choose a proper cutoff to analyze the open time because there are very few ATP-dependent closed events and they somewhat overlap with the ATP-independent ones. We used the same cutoff time of 500 ms to construct the open time histogram (Fig. 6 F). Since the channel is locked open most of the time, the number of events is not large enough for a more rigorous quantitative analysis even with ∼100 min of single-channel recording. Nevertheless, the distribution appears to have three components with roughly similar time constants as those obtained at 10 μM ATP (compare Fig. 6 D). Yet, the proportion of these three open events is very different from that at 10 μM ATP. While, at 10 μM ATP, most of the locked-open state is of the short one (LOS), at 1 mM ATP, the longer locked-open state (LOL) contributes >50% of the events. This result shows that an increase in [ATP] shifts the relative distribution of these two locked-open states, supporting the idea that occupancy of an ATP binding site stabilizes the locked-open state. It should be noted that, even disregarding the fitted curves, we can still visualize a rightward shift of the open time distribution at 1 mM ATP (Fig. 6, compare D and E).
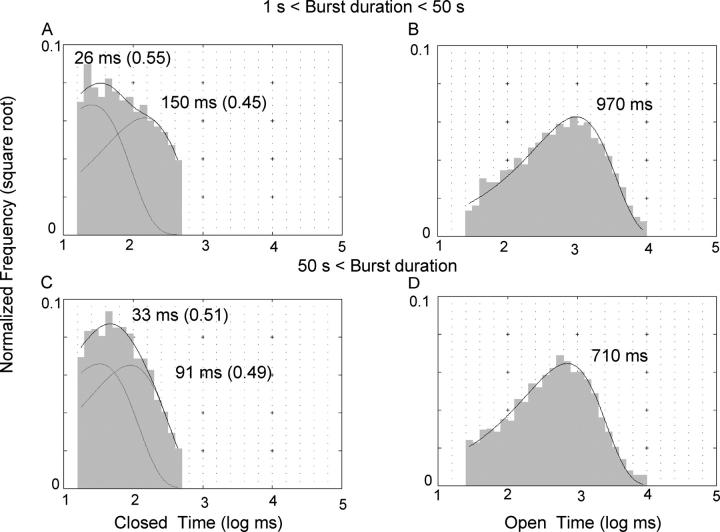
To further elaborate the kinetic mechanism of the two locked-open states (LOS and LOL), we analyzed dwell-time distributions within the locked-open bursts that were collected at 10 μM ATP. We used 50 s as the cutoff value to differentiate these two locked-open states. Both types of bursts show similar features. There are two types of closings within the burst, the flickers (CF closed state) with a characteristic time constant of 20–30 ms, and longer closings (CL closed state) with a time constant of ∼100 ms (Fig. 7, A and C). Although the physical meaning of the longer closings (CL closed state) within a locked-open burst is unclear, the flickery closings (CF closed state) are likely due to a blockade of the channel (Zhou et al., 2001). To obtain the transition rates in and out of the CL closed state, we used 50 ms as a cutoff to analyze the open time distributions within the short and long locked-open bursts. The resulting open time constants are not very different for both types of bursts (Fig. 7, B and D).
Figure 7.
Intraburst kinetic analysis. Locked-open bursts were divided into two categories: short-lived locked-open events (1–50 s in length) and long-lived locked-open events (>50 s). Both types of bursts show similar characteristics. The closed dwell time histograms (A and C) show two components: the flickers (20–30 ms) and a relatively longer closing (∼100 ms). Once the flickering closures are removed by using a 50-ms cutoff, the open times within the locked-open bursts are very similar, irrespective of the locked-open duration (B and D).
ATP Concentration Dependence of E1371S-CFTR Current Relaxations
Before we attempt to specify to which NBD ATP binds to affect the stability of the open state, we need to be sure that the [ATP] dependence of the open state stability is not solely due to deletion of the R domain. We therefore characterized the current relaxation for the E1371S mutation in the WT background. Fig. 8 A shows a continuous current trace in response to 10 μM and 1 mM ATP. PKA is added in the solution to ensure adequate phosphorylation. Unlike ΔR/E1371S-CFTR, the E1371S mutants in the WT background express very well. Most of our patches yield tens or hundreds of pA currents, which allow better curve fitting for ensemble macroscopic currents.
Figure 8.
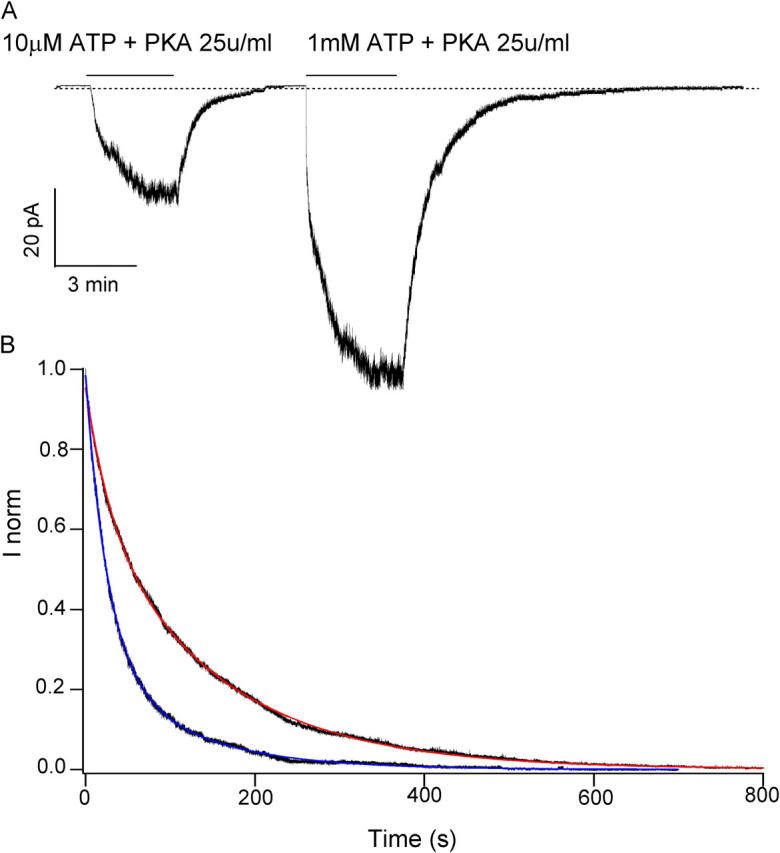
Macroscopic current relaxation of E1371S-CFTR currents. (A) Sample trace of current relaxations for E1371S-CFTR channels activated with 10 μM ATP + PKA, or with 1 mM ATP + PKA. (B) Normalized ensemble current relaxations upon removal of 1 mM ATP (from 12 patches) or 10 μM ATP (from 9 patches). The 1 mM ATP relaxation curve can be fitted with a double exponential function (red curve) with time constants of 149.3 ± 0.02 s (69%) and 29.59 ± 0.02 s (31%). The 10 μM ATP curve can be fitted also with a double exponential function (blue curve) with time constants of 107.53 ± 0.08 s (29%), and 26.32 ± 0.01 s (71%).
Current relaxations upon removal of 1 mM ATP can be better fitted with a double exponential function with relaxation time constants of 149.30 ± 0.02 s (69%) and 29.59 ± 0.02 s (31%). At 10 μM ATP concentration, the current decay also follows a double exponential time course. Although the values of resulting time constants 107.53 ± 0.08 s (29%) and 26.32 ± 0.01 s (71%) are similar to those obtained at 1 mM ATP, the relative proportion of these two components is very different. These results again suggest that increasing [ATP] shifts the distribution of two locked-open states. We would like to point out that the relaxation curve obtained for the ΔR/E1371S mutant (Fig. 2 B) shows only one exponential decay (τ = 100 s) at 1 mM. This discrepancy is likely due to the fact that the absolute amplitude of ensemble current for ΔR/E1371S-CFTR, even with pooling of 47 patches, is still much smaller (∼85 pA) than the macroscopic currents obtained with the E1371S mutant in the WT background (∼580 pA). Therefore, the minor fast component of the exponential decay is difficult to resolve in the ΔR/E1371S-CFTR.
When performing the relaxation experiments in E1371S-CFTR channels, after several minutes of washout, we can still observe a single channel that remains open (Fig. 9). Within this long burst after ATP is removed, we can distinguish the brief flickery closings and also some slightly longer closings, similar to those with the intermediate closed time constant described above (Fig. 6). We pooled four single-channel locked-open bursts (the last channel still open in the relaxation experiments) and analyzed the closed time distribution within the burst. We found that there are two characteristic closed events with time constants of ∼20 and ∼80 ms, both very similar to the values described above. Since these two closed events are observed in the complete absence of ATP, we conclude that neither of them is ATP dependent.
Figure 9.
Kinetic analysis of the last E1371S-CFTR channel that remains open after removal of ATP. (A) Sample trace of the current relaxation of E1371S-CFTR channels upon ATP washout. The inset shows the expanded trace of the last channel that remains open. Note the presence of poorly resolved flickers and several long closings that last for hundreds of milliseconds. (B) Data from four patches were pooled together to construct the closed time histogram.
Current Relaxations of the K464A/E1371S Mutant
According to the most recent model (Scheme 2 in the accompanying paper) for CFTR gating (Vergani et al., 2003), NBD1 has little role in the gating transitions since the off rate is extremely slow, and ATP binding at NDB2 precedes channel opening. Our data showing that ADP competitively inhibits CFTR opening (Fig. 6 in Bompadre et al., 2005) can be explained if ADP binds at NBD2 to serve this role. However, if ADP binding at NBD2 prevents channel opening, it would be difficult to envision that ADP binds to the same site to affect the stability of the open state. In addition, Vergani's model predicts that the open time should not depend on either [ATP] or the presence of ADP. Clearly, this is not the case. To explain our data we should consider the possibility that the occupancy of ATP at NBD1 affects the stability of the open state. This hypothesis could account for both the ADP effect on the open time and [ATP]-dependent shift of the distribution of the two locked-open states (see discussion for details).
Since the locked-open time is much shorter when ADP is bound than that with ATP bound, we speculate that the binding energy of ATP (or ADP) contributes to the overall energetics of the locked-open state conformation. This hypothesis predicts that a mutation at NBD1 that lowers the binding strength of ATP will have a shorter locked-open time. The crystal structure of CFTR's NBD1 reveals that the Walker A lysine, K464, coordinates the β- and γ-phosphates of the bound ATP (Lewis et al., 2004). Mutation of this lysine has been shown to lower the ATP binding affinity at NBD1 (Basso et al., 2003). Since the K464 mutation has a mild trafficking defect (Cheng et al., 1990; unpublished data), and ΔR-CFTR already suffers from low expression, we decided to make the K464A/E1371S double mutant construct in the WT background.
Relaxation experiments were performed in excised inside-out patches as shown in Fig. 10 A. The current decay of the K464A/E1371S-CFTR channel currents is indeed faster than that of E1371S-CFTR, resulting in a shorter relaxation time constant (19.60 ± 0.01 s) upon washout of 1 mM ATP (Fig. 10 B). This relaxation time constant is even shorter when the K464A/E1371S-CFTR channel is opened with 10 μM ATP (13.95 ± 0.02 s). Since the number of K464A/E1371S-CFTR channels is relatively low due to a moderate trafficking defect, it is easier to observe microscopic channel behavior at 10 μM ATP (Fig. 10 C). As shown previously for ΔR/E1371S-CFTR (Fig. 5), the current trace reveals that K464A/E1371S-CFTR channels also exhibit numerous brief openings that last for tens to hundreds of milliseconds in the presence of 10 μM ATP. Thus, these brief openings for a mutant CFTR with defective ATP hydrolysis are not due to the removal of the R domain, but are true characteristics of the hydrolysis-deficient mutant CFTR.
Figure 10.
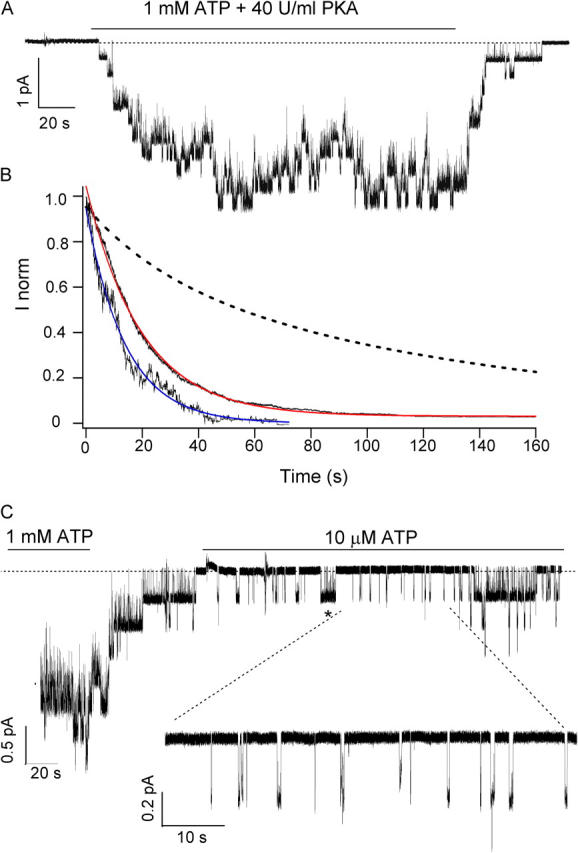
The K464A mutation shortens the locked-open time of E1371S-CFTR. (A) Sample trace of K464A/E1371S-CFTR channels in the presence of 1 mM ATP + PKA. Note that the relaxation upon nucleotide washout is very fast. (B) Ensemble macroscopic currents were generated from 18 patches. The macroscopic current has a relaxation time constant of 19.60 ± 0.01 s (red curve). (C) Sample trace of K464A/E1371S-CFTR channels in the presence of 10 μM ATP (blue curve). The inset shows the presence of numerous brief openings (from 42 to 650 ms). Note also the presence of longer openings (*, 9 s).
Characterization of the Brief Openings
In the presence of micromolar ATP, we observed the occurrence of numerous brief openings. To decide whether these openings are ATP dependent, we first quantitatively estimate the kinetics of spontaneously opened channel in the complete absence of ATP.
We chose the ΔR background because of its resistance to rundown. The fact that removal of the R domain renders the channel phosphorylation independent also helps to avoid a potential technical problem of ATP contamination in the recording system. Excised inside-out patches from cells expressing ΔR/E1371S-CFTR channels were exposed to ATP-free perfusion solution for >5 min to determine the opening rate of spontaneous opening events. The patches were then exposed to 1 mM ATP to determine the number of channels present. Fig. 11 A shows a representative experiment. Although this patch contains many channels, there are only ∼20 opening events in the ∼5-min period without ATP. The calculated opening rate is 0.005 s−1. We used survival plot analysis to obtain the mean open time for these spontaneous opening events. The distribution can be fitted well with a single exponential function with a mean open time of ∼430 ± 19 ms (Fig. 11 C). We repeated the same experiment with ΔR-CFTR channels (Fig. 11 B). We measured the open time of the spontaneous openings from six patches and constructed a survivor plot to obtain the mean open time. Note that despite 38 min of recording, the number of events is still very small. A fit with an exponential function gives a mean open time of 485 ± 24 ms (Fig. 11 D). The calculated spontaneous opening rate is 0.006 s−1. Thus, mutating the E1371 residue has little effect on the spontaneous opening rate. Although the E1371S mutation increases the lifetime of ATP-opened channel by >100-fold, it only minimally affects the open time constant for these spontaneous opening events.
Figure 11.
Kinetic analysis of the spontaneous openings in the absence of ATP. (A) A representative ΔR/E1371S-CFTR current trace from an excised inside-out patch exposed to ATP-free solution for several minutes before 1 mM ATP was applied. (B) Similar experiment as described in A, but with ΔR-CFTR channels. The open times of these spontaneous openings from several patches containing ΔR/E1371S-CFTR (C) or ΔR-CFTR (D) were pooled together to construct survivor plots.
Despite the similarity between these open time constants for the spontaneous openings and the brief open time constant for the ΔR/E1371S-CFTR in the presence of 10 μM ATP (Fig. 6 D), it is doubtful that the observed events at 10 μM ATP solely come from spontaneous openings because they appear more frequently than the spontaneous openings. We then quantify the kinetic step to the brief opening events using the ΔR/E1371S-CFTR data in the presence of 10 μM ATP. We measured the closed time preceding all openings <300 ms and constructed a prebursting closed time histogram. This histogram was fitted with an exponential function resulting in a time constant of 6.6 s, representing the average closed time before a brief opening. This closed time constant corresponds to an opening rate of 0.17 s−1, a number over 30 times higher than the one obtained for the spontaneous openings. This observation strongly supports the notion that a significant fraction of the brief openings are induced by ATP.
DISCUSSION
Macroscopic and Microscopic Kinetic Analyses of CFTR Gating
Two different assays, single-channel dwell-time analysis and macroscopic current relaxations, have been used throughout this work in order to understand how nucleotide binding/hydrolysis controls CFTR gating. We are especially interested in how nucleotide binding affects the stability of the open state. These two techniques complement each other very well. Some discussions about the pros and cons of each method are warranted before we elaborate the kinetic and structural significance of our results.
We used macroscopic current relaxation upon nucleotide removal to quantify the locked-open times for E1371S mutant CFTR. Although our solution change has a deadtime of ∼3 s, most of the relaxation time constants for this mutant can be measured accurately because of the long locked-open time on the order of tens to hundreds of seconds. The measured relaxation time constants reflect only the closing rate of the locked-open channel since, in the absence of ATP, the channel seldom opens, and even when it opens, it does not sojourn to the locked-open state (Fig. 11). Multiple components of the current relaxation represent the presence of multiple locked-open states. The most attractive feature of this type of analysis is that no model or artificial cutoffs need to be set. The raw data are fitted with no a priori assumptions. The main disadvantage is that this approach requires very large currents, especially when trying to discern multiple relaxation time constants that differ by less than an order of magnitude.
Macroscopic current relaxations were also used to demonstrate the existence of a second locked-open state in the presence of ADP. From single-channel analysis, all we could observe was a shortening of the mean open time for ΔR- (Bompadre et al., 2005) or ΔR/D1370N-CFTR (Fig. 1). In contrast, the macroscopic current relaxation of ΔR/E1371S-CFTR clearly shows the presence of two components in the relaxation once the channels are opened by ATP plus ADP (Fig. 2), strongly suggesting the presence of two different locked-open states. Furthermore, the relaxation of E1371S-CFTR channel currents in the presence of different ATP concentrations reveals the presence of two locked-open states, and an [ATP]-dependent shift in the distribution of each state (confirmed by ΔR/E1371S single-channel data). These results, without assuming any kinetic model, indicate that nucleotide binding affects the stability of the locked-open state.
Perhaps because of a much smaller current amplitude, we did not resolve two relaxation time constants in the presence of 1 mM ATP for ΔR/E1371S-CFTR channels. If we accept the fact that multiple locked-open states do exist for ΔR/E1371S mutants at 1 mM ATP as shown by the single-channel analysis (Fig. 6), how can we ascertain that ADP induces another locked-open state rather than simply increases the relative occupancy of the short-lived locked-open state? In theory, we cannot differentiate these two possibilities unless a triple exponential current decay is observed with the presence of ADP. As long as the lifetime of the ADP-bound locked-open state is not very different from the short locked-open state, it will be very difficult, if not impossible, to dissect these two time constants. It should be noted that the fraction of short-lived locked-open state (LOS) is small at 1 mM ATP (<30%, Figs. 6 and 8). Nevertheless, in the presence of ADP, the short-lived component upon current relaxation is responsible for 50% of the entire current relaxation, indicating that binding of ADP does affect the lifetime of the locked-open state.
Microscopic kinetic analysis, on the other hand, offers the advantage that individual opening and closing events can be analyzed over a long period of time to extract individual time constants. Unfortunately, the gating of CFTR channels is slow, and for hydrolysis-deficient mutants, it is even slower. Thus, very long recordings are needed to collect enough number of events to perform rigorous kinetic analysis. Although the ΔR construct provides a unique advantage of being dephosphorylation resistant, pooling data from different patches is still an inevitable solution. Cutoffs or predetermined gating models need to be used while analyzing the data, especially for recordings from patches containing multiple channels. The imperfect solution of assuming a gating model for data analysis (e.g., Csanády, 2000) probably explains why the effects of ADP on the open time constant are not detected in multichannel analysis (Fig. 7 C in Bompadre et al., 2005). Another technical hurdle for single-channel kinetic analysis is the small conductance of CFTR. Heavy filtering of the data is often necessary to secure a reasonable signal/noise ratio. Although this has not been a problem for quantifying ATP-dependent gating since the relevant events are on the order of hundreds of milliseconds to seconds, heavy filtering inevitably results in a poor resolution of the brief ATP-independent events.
By collecting single-channel events from several patches containing ΔR-CFTR, we observed the effect of ADP on the mean open time (Fig. 8 in Bompadre et al., 2005). Using similar dwell time analysis, we were able to detect multiple components in open time histograms (Fig. 6) for ΔR/E1371S mutants. An ATP-dependent shift of the distribution of these openings corroborates with the results of macroscopic current relaxations. Therefore, despite all the limitations discussed above, integrating both macroscopic and microscopic analyses of our data, we reach an unremitting conclusion that nucleotide binding affects the relative distribution of different (locked) open states.
Multiple Open States
The results presented in the current study indicate the presence of multiple open states. The distribution of these opens states changes as [ATP] is changed. The [ATP]-dependent shift of the distribution of two locked-open states can be better explained by the idea, as proposed above, that ATP binding at NBD1 affects the stability of the locked-open state. As [ATP] is increased, the fraction of channels with NBD1 occupied by ATP will increase. We propose that channels with both NBDs occupied with ATP will exhibit a longer locked-open time than the singly occupied channels to explain how changing [ATP] shifts the distribution of these two different locked-open states. This same idea can also explain ADP's effects on the current relaxation of ΔR/E1371S mutants (Fig. 2). If the locked-open state with ADP binding at NBD1 is less stable than in the case of ATP binding, we will then expect the presence of a shorter locked-open time with ADP. Although we were not able to resolve two open time constants for ΔR-CFTR in the presence of ADP (Fig. 8 in Bompadre et al., 2005), it seems reasonable to speculate that the same mechanism may apply in WT-CFTR when ATP hydrolysis is intact.
In addition to two locked-open states, single-channel recordings also show a brief opening that lasts for ∼300 ms. A similar short-lived open state was reported previously for K1250A-CFTR (τo = ∼250 ms), another hydrolysis-deficient mutant (Zeltwanger et al., 1999). Vergani et al. (2003) proposed that this unstable open state represents spontaneous opening in the absence of ATP. Indeed, the mean lifetime of the spontaneous openings for ΔR/E1371S is ∼400 ms. However, at 10 μM ATP, the frequency of these short-lived events is higher than in the absence of ATP. ATP binding at NBD(s) must also contribute to the appearance of these events in the presence of 10 μM ATP.
Distinct Roles of NBDs in CFTR Gating
Although the data shown in the current report were mostly obtained from studies of CFTR mutants, we will extend these results to get a glimpse of how normal gating occurs. First, we propose that ATP binding at NBD2 plays a major role in channel opening. This idea is based on the observation that mutating the Walker A lysine, K464, at NBD1 does not affect the opening rate (Powe et al., 2002), although this residue is involved in coordinating bound ATP (Lewis et al., 2004) and the same mutation lowers the ATP binding affinity at NBD1 (Basso et al., 2003). Second, hydrolysis of bound ATP at NBD2 and subsequent dissociation of ADP and Pi drives channel closing. This idea is supported by the demonstration that WT CFTR gating shows kinetics that demands an input of free energy (Zeltwanger et al., 1999). Furthermore, mutations that abolish ATP hydrolysis (e.g., K1250A and E1371S) dramatically prolong the open state (Gunderson and Kopito, 1995; Zeltwanger et al., 1999; Powe et al., 2002; Vergani et al., 2003). Third, ligand binding at NBD1 can modulate the stability of the open state. Powe et al. (2002) showed that the K464A mutation shortens the open time by 40% at high [ATP]. Interestingly, introducing the K464A mutations into the K1250A construct significantly decreases the locked-open time (Powe et al., 2002; Vergani et al., 2003). An equivalent observation is also made in the current report for K464A/E1371S mutants. Fourth, contrary to the model proposed by Vergani et al. (2003), ATP binding at NBD1 is not required for channel opening. The fact that the channel can open in the complete absence of ATP already indicates that ATP binding at neither NBD is absolutely required for channel opening. As mentioned above, Powe et al. (2002) showed that the K464A mutant exhibits a normal opening rate despite a lower ATP binding affinity at NBD1 for this mutant. Furthermore, we interpret the [ATP]-dependent shift of the distribution of two locked-open states by proposing that the occupancy of NBD1 affects the stability of the locked-open state. Therefore, the shorter locked-open time represents an open state with ATP bound at NBD2 while NBD1 is vacant.
Structural Implications
Crystal structures of bacterial NBDs (e.g., Smith et al., 2002; Chen et al., 2003) show a head-to-tail dimeric configuration. The two ATP-binding sites are buried at the dimer interface. The bound ligands as well as several amino acid residues participating in nucleotide interactions are intimately involved in forming a stable dimer. The dimer structure not only explains numerous biochemical data (e.g., Fetsch and Davidson, 2003), but also places the signature motif (LSGGQ) that defines the ABC transporter family at the dimer interface actively involved in interactions with ATP. Importantly, this head-to-tail configuration of NBD dimers corroborates with the holoenzyme structure of Escherichia coli BtuCD protein (Locher et al., 2002).
Although so far there is no structural evidence that equivalent dimerization of CFTR's NBDs occurs during gating transitions, we have proposed that the open state of the channel may be associated with a dimerized configuration of NBDs (Powe et al., 2002). This hypothesis is based on the observation that mutations that affect ATP binding at NBD1 (e.g., K464A) alter the stability of the open state of K1250A, suggesting an interaction between two ATP-binding sites. An NBD1–NBD2 dimer with two ATP binding pockets sandwiched at the dimer interface seems a reasonable model to explain this result. Taking one step further, Vergani et al. (2003) proposed a strict coupling of NBD dimerization/dissociation to channel opening and closing. More recently, using mutant cycle analysis, Vergani et al. (2005) provided evidence for a direct interaction between R555 (in NBD1) and T1246 (in NBD2) in the open state. This new result strongly supports the idea that an NBD1–NBD2 dimer is associated with the open state.
In light of these new findings, we feel compelled to make several structural implications of our results. First, in all the dimer structures published so far, there are extensive hydrogen bonds and van der Waals interactions between ATP and Walker A and B sequences in one subunit, and between ATP and the LSGGQ motif in the other subunit (Smith et al., 2002; Chen et al., 2003). These extensive binding forces suggest that the dimer is an energetically stable state. Thus, it seems reasonable to propose that ATP binding elicits a large degree of molecular motion that involves closing of the dimer interface and that only hydrolysis of bound ATP could provide sufficient energy to destabilize the dimer (Hopfner et al., 2000; Smith et al., 2002). Indeed, the hydrolysis-deficient mutant, e.g., E1371S-CFTR, can assume a locked-open state for minutes, whereas WT channels only open for hundreds of milliseconds.
Second, once the dimer forms in the presence of high [ATP], two ATP molecules are sandwiched at the dimer interface (Smith et al., 2002; Chen et al., 2003). Thus, the binding energy of the ligand should contribute significantly to the overall energy of the dimer. Weakening the binding energy is expected to shorten the lifetime of the dimer. This can be achieved by using a smaller ligand, such as ADP, by keeping the binding site empty (e.g., at low [ATP]), or by mutating the binding partner in the NBD. In the current report, we show that the locked-open time of the E1371S mutant can be significantly shortened by all three maneuvers.
Third, in the absence of ATP, the spontaneous opening rate for our ΔR constructs is ∼0.006 s−1, and the mean lifetime of these spontaneous opening events is ∼400 ms. If the spontaneous openings reflect an ATP-independent dimerization reaction, then these kinetic parameters may explain why the dimer is not detected biochemically in the absence of ATP (Moody et al., 2002). Furthermore, from the energetic point of view, the absence of ligands at the dimer interface may also explain the short-lived openings observed for ΔR/E1371S-CFTR in the absence of ATP.
Unsettled Issues
One of the unsettled issues is the mechanism of short-lived openings of ΔR/E1371S-CFTR that appear frequently in the presence of micromolar ATP. Admittedly, some of these events are due to spontaneous, ATP-independent openings. However, the opening rate to these brief openings in the presence of 10 μM ATP, ∼0.17 s−1, is much larger than the spontaneous opening rate (∼0.006 s−1), suggesting that most of them are ATP dependent. We do not know to which NBDs ATP binds to increase the opening rate to this short-lived state. However, the extensive molecular interactions at the dimer interface suggest that the actual dimerization reaction takes multiple steps. Then, this short-lived open state could represent a transitional unstable dimer before an energetically stable dimer is formed. Perhaps ATP binding to either NBD or even both NBDs will increase the rate toward this state.
Although we proposed that ATP binding at NBD2 plays a critical role in channel opening (see above), this idea is based more on default since we observed that the K464A mutation, which decreases ATP binding affinity at NBD1 (Basso et al., 2003), does not affect the opening rate (Powe et al., 2002). While we did observe a decrease of the opening rate by the K1250A mutation (Powe et al., 2002; cf. Vergani et al., 2003), this mutation at NBD2 likely affects both ATP binding and hydrolysis. To establish the role of ATP binding at NBD2 in controlling channel opening, future experiments need to identify amino acid residues, mutations of which only affect the ATP binding step.
Our demonstration of the presence of multiple open states already suggests that opening and closing of the CFTR channel is more complicated than a simple association/dissociation of NBD dimer. The presence of ATP-independent closed state further compounds the picture. By examining single-channel kinetics within a locked-open event, we observed an unexpected closed state with a mean lifetime of ∼100 ms (Fig. 9). This closed state is at least threefold more stable than the voltage-dependent flickery closings (Zhou et al., 2001). The lifetime of this novel closed state is not voltage dependent (unpublished data) and these closings are present even after ATP is completely removed, suggesting that they are ATP independent. If a locked-open state represents a tight dimer configuration as proposed by Vergani et al. (2005), the presence of numerous transitions in and out of this ATP-independent closed state within a locked-open event indicates that the physical gate of CFTR can still open and close when a stable dimer is formed. This apparently violates the strict coupling hypothesis (Vergani et al. 2003). On the other hand, if the strict coupling hypothesis is correct, this closed state may represent a transitional, partially separated dimer where ATP remains bound. In this latter scenario, the NBD dimer more likely assumes a dynamic and unexpectedly flexible structure.
Single-channel kinetic analysis of the ΔR/E1371S-CFTR mutant also revealed two ATP-dependent closed states (Fig. 6, A and B). If our hypothesis that both NBDs are involved in CFTR gating is correct, as a minimum, two different configurations of the ATP-binding sites should exist: one with both sites vacant and the other with one site occupied. Since at least one of the ATP-binding sites is vacant in these two states, by definition, their lifetimes have to be ATP dependent. At millimolar [ATP], however, we only observe one long closed time constant probably because the channel has one of the binding sites (likely NBD1) occupied most of the time, and therefore, once the channel closes, the opening is initiated by ATP binding at NBD2. This latter, more restricted, scenario is actually very close to the model proposed by Vergani et al. (2003). Considering the difficulty of kinetically dissecting different ATP-dependent closed states, we are currently seeking independent methods to verify the existence of these states.
Our kinetic analyses and structural interpretations were all based on studies of hydrolysis-deficient mutant CFTR. Abolition of the ATPase activity by mutagenesis provides the advantage that CFTR can now be treated as a classical ligand-gated channel. If ATP hydrolysis dominates the closing transition for WT-CFTR gating, as described above, some of the closed states revealed in the current studies may not be discerned. Future studies of WT-CFTR gating at lower temperatures may confirm some of our findings. In this regard, the ΔR-CFTR construct used in the current study could again be very valuable.
A difference in closing transitions between WT and hydrolysis-deficient mutant CFTR may also explain the conundrum that ADP exerts a much larger effect on the locked-open time of ΔR/E1371S channels than on the open time of the ΔR channels**.** A much larger free energy is involved when ATP hydrolysis is used to close the channel. Thus the binding energy of nucleotide at NBD1 is relative small compared with the energy released from ATP hydrolysis. On the other hand, in E1371S-CFTR whose hydrolysis is abolished, thermoenergy is used for channel closing. Then the binding energy of nucleotide at NBD1 plays a more important role in deciding the rate of channel closing.
Conclusive Remarks
The most important conclusion from this study is that the gating of CFTR is more complicated than previously believed because we have demonstrated multiple open states and multiple closed states, both of which are affected by occupancy of nucleotides at each NBD. In view of this complexity, it is perhaps advisable to study CFTR gating from a reductionist point of view. It may be more fruitful in the near future to focus on quantifying limited kinetic steps rather than on elaborating a complete gating scheme.
Supplemental Material
Supplemental Material Index
Acknowledgments
We are grateful to Drs. Kevin Gillis and Joseph Mindell for their critical reading of the manuscript. We thank Cindy Chu for technical assistance.
This work is supported by the National Institutes of Health (T.C. Hwang, DK55835, HL53445; X. Zou, DK61529) and a beginning Grant-in-Aid from the American Heart Association (X. Zou). S.G. Bompadre is a recipient of NRSA (DK062565). Y. Sohma is supported by the Japan Society for the Promotion of Science (15590196).
Olaf S. Andersen served as editor.
Abbreviations used in this paper: ABC, ATP-binding cassette; CFTR, cystic fibrosis transmembrane conductance regulator; NBD, nucleotide binding domain; WT, wild-type.
References
- Ai, T., S.G. Bompadre, X. Wang, S. Hu, M. Li, and T.-C. Hwang. 2004. Capsaicin potentiates wild-type and mutant CFTR chloride channel currents. Mol. Pharmacol. 65:1415–1426. [DOI] [PubMed] [Google Scholar]
- Aleksandrov, A.A., and J.R. Riordan. 1998. Regulation of CFTR ion channel gating by Mg-ATP. FEBS Lett. 431:97–101. [DOI] [PubMed] [Google Scholar]
- Aleksandrov, A.A., X.B. Chang, L. Aleksandrov, and J.R. Riordan. 2000. The non-hydrolytic pathway of cystic fibrosis transmembrane conductance regulator ion channel gating. J. Physiol. 528:259–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basso, C., P. Vergani, A.C. Nairn, and D.C. Gadsby. 2003. Prolonged nonhydrolytic interaction of nucleotide with CFTR's NH2-terminal nucleotide binding domain and its role in channel gating. J. Gen. Physiol. 122:333–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bompadre S.G., T. Ai, J.H. Cho, X. Wang, Y. Sohma, M. Li, and T.-C. Hwang. 2005. CFTR gating I: characterization of the ATP-dependent gating of a phosphorylation-independent CFTR channel (ΔR-CFTR). J. Gen. Physiol. 125:361–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carson, M.R., S.M. Travis, and M.J. Welsh. 1995. The two nucleotide-binding domains of cystic fibrosis transmembrane conductance regulator (CFTR) have distinct functions in controlling channel activity. J. Biol. Chem. 270:1711–1717. [DOI] [PubMed] [Google Scholar]
- Chen, J., G. Lu, J. Lin, A.L. Davidson, and F.A. Quiocho. 2003. A tweezers-like motion of the ATP-binding cassette dimer in an ABC transports cycle. Mol. Cell. 12:651–661. [DOI] [PubMed] [Google Scholar]
- Cheng, S.H., R.J. Gregory, J. Marshall, S. Paul, D.W. Souza, G.A. White, C.R. O'Riordan, and A.E. Smith. 1990. Defective intracellular transport and processing of CFTR is the molecular basis of most cystic fibrosis. Cell. 63:827–834. [DOI] [PubMed] [Google Scholar]
- Csanády, L. 2000. Rapid kinetic analysis of multichannel records by a simultaneous fit to all dwell-time histograms. Biophys. J. 78:785–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diederichs, K., J. Diez, G. Greller, C. Muller, J. Breed, C. Schnell, C. Vonrhein, W. Boos, and W. Welte. 2000. Crystal structure of MalK, the ATPase subunit of the trehalose/maltose ABC transporter of the archaeon Thermococcus litoralis. EMBO J. 19(22):5951–5961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetsch, E.E., and A.L. Davidson. 2003. Maltose transport through the inner membrane of E. coli. Front. Biosci. 8:d652–d660. [DOI] [PubMed] [Google Scholar]
- Gadsby, D.C., and A.C. Nairn. 1999. Control of CFTR channel gating by phosphorylation and nucleotide hydrolysis. Physiol. Rev. 79:S77–S107. [DOI] [PubMed] [Google Scholar]
- Gaudet, R., and D.C. Wiley. 2001. Structure of the ABC ATPase domain of human TAP1, the transporter associated with antigen processing. EMBO J. 20:4964–4972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunderson, K.L., and R.R. Kopito. 1995. Conformational states of CFTR associated with channel gating: the role of ATP binding and hydrolysis. Cell. 82:231–239. [DOI] [PubMed] [Google Scholar]
- Hopfner, K.P., A. Karcher, D.S. Shin, L. Craig, L.M. Arthur, J.P. Carney, and J.A. Tainer. 2000. Structural biology of Rad50 ATPase: ATP-driven conformational control in DNA double-strand break repair and the ABC-ATPase superfamily. Cell. 101:789–800. [DOI] [PubMed] [Google Scholar]
- Hung, L.W., I.X. Wang, K. Nikaido, P.Q. Liu, G.F. Ames, and S.H. Kim. 1998. Crystal structure of the ATP-binding subunit of an ABC transporter. Nature. 396(6712):703–707. [DOI] [PubMed] [Google Scholar]
- Karpowich, N., O. Martsinkevich, L. Millen, Y.R. Yuan, P.L. Dai, K. MacVey, P.J. Thomas, and J.F. Hunt. 2001. Crystal structures of the MJ1267 ATP binding cassette reveal an induced-fit effect at the ATPase active site of an ABC transporter. Structure (Camb). 9:571–586. [DOI] [PubMed] [Google Scholar]
- Lewis, H.A., S.G. Buchanan, S.K. Burley, K. Conners, M. Dickey, M. Dorwart, R. Fowler, X. Gao, W.B. Guggino, W.A. Hendrickson, et al. 2004. Structure of nucleotide-binding domain 1 of the cystic fibrosis transmembrane conductance regulator. EMBO J. 23:282–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Locher, K.P., A.T. Lee, and D.C. Rees. 2002. The E. coli BtuCD structure: a framework for ABC transporter architecture and mechanism. Science. 296:1091–1098. [DOI] [PubMed] [Google Scholar]
- Moody, J.E., L. Millen, D. Binns, J.F. Hunt, and P.J. Thomas. 2002. Cooperative, ATP-dependent association of the nucleotide binding cassettes during the catalytic cycle of ATP-binding cassette transporters. J. Biol. Chem. 277:21111–21114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powe, A., L. Al-Nakkash, M. Li, and T.-C. Hwang. 2002. Mutation of Walker-A lysine 464 in cystic fibrosis transmembrane conductance regulator reveals functional interaction between its nucleotide binding domains. J. Physiol. 539:333–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt, L., H. Benabdelhak, M.A. Blight, I.B. Holland, and M.T. Stubbs. 2003. Crystal structure of the nucleotide-binding domain of the ABC-transporter haemolysin B: identification of a variable region within ABC helical domains. J. Mol. Biol. 330:333–342. [DOI] [PubMed] [Google Scholar]
- Smith, P.C., N. Karpowich, L. Millen, J.E. Moody, J. Rosen, P.J. Thomas, and J.F. Hunt. 2002. ATP binding to the motor domain from an ABC transporter drives formation of a nucleotide sandwich dimer. Mol. Cell. 10:139–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabo, K., G. Szakacs, T. Hegeds, and B. Sarkadi. 1999. Nucleotide occlusion in the human cystic fibrosis transmembrane conductance regulator. Different patterns in the two nucleotide binding domains. J. Biol. Chem. 274:12209–12212. [DOI] [PubMed] [Google Scholar]
- Tao, T., J. Xie, M.L. Drumm, J. Zhao, P.B. Davis, and J. Ma. 1996. Slow conversions among subconductance states of cystic fibrosis transmembrane conductance regulator chloride channel. Biophys. J. 70:743–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdon, G., S.V. Albers, B.W. Dijkstra, A.J. Driessen, and A.M. Thunnissen. 2003. Crystal structures of the ATPase subunit of the glucose ABC transporter from Sulfolobus solfataricus: nucleotide-free and nucleotide-bound conformations. J. Mol. Biol. 330:343–358. [DOI] [PubMed] [Google Scholar]
- Vergani, P., A.C. Nairn, and D.C. Gadsby. 2003. On the mechanism of MgATP-dependent gating of CFTR Cl− channels. J. Gen. Physiol. 121:17–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergani, P., S.W. Lockless, A.C. Nairn, and D.C. Gadsby. 2005. CFTR channel opening by ATP-driven tight dimerization of its nucleotide binding domains. Nature. 433:876–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, F., S. Zeltwanger, I. Yang, A. Nairn, and T.-C. Hwang. 1998. Action of genistein on CFTR gating: evidence of two binding sites with opposite effects. J. Gen. Physiol. 111:477–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan, Y.R., S. Blecker, O. Martsinkevich, L. Millen, P.J. Thomas, and J.F. Hunt. 2001. The crystal structure of the MJ0796 ATP-binding cassette. Implications for the structural consequences of ATP hydrolysis in the active site of an ABC transporter. J. Biol. Chem. 276:32313–32321. [DOI] [PubMed] [Google Scholar]
- Zeltwanger, S., F. Wang, G.T. Wang, K.D. Gillis, and T.-C. Hwang. 1999. Gating of cystic fibrosis transmembrane conductance regulator chloride channels by adenosine triphosphate hydrolysis. Quantitative analysis of a cyclic gating scheme. J. Gen. Physiol. 113:541–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, Z., S. Hu, and T.-C. Hwang. 2001. Voltage-dependent flickery block of an open cystic fibrosis transmembrane conductance regulator (CFTR) channel pore. J. Physiol. 532:435–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Material Index