The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model (original) (raw)
Abstract
We investigated the gene coexpression network in Saccharomyces cerevisiae, in which genes are linked when they are coregulated. This network is shown to have a scale-free, small-world architecture. Such architecture is typical of biological networks in which the nodes are connected when they are involved in the same biological process. Current models for the evolution of intracellular networks do not adequately reproduce the features that we observe in the network. We therefore derive a new model for its evolution based on the observation that there is a positive correlation between the sequence similarity of paralogues and their probability of coexpression or sharing of transcription factor binding sites (TFBSs). The simple, neutralist's model consists of (1) coduplication of genes with their TFBSs, (2) deletion and duplication of individual TFBSs and (3) gene loss. A network is constructed by connecting genes that share multiple TFBSs. Our model reproduces the scale-free, small-world architecture of the coregulation network and the homology relations between coregulated genes without the need for selection either at the level of the network structure or at the level of gene regulation.
Keywords: modelling, network, coexpression, gene duplication, molecular evolution
Introduction
Unravelling the interactions between the elements of a cell constitutes a major goal of the genome era. The structure of the resulting interaction networks is relevant to the functioning of the cell, for example, in development (Davidson et al, 2003), and for the interpretation of experimental results. Network analyses have shown a correlation between, on the one hand, the essentiality of a gene and, on the other hand, either the number of connections that the gene has (Jeong et al, 2001) or the topology of the metabolic network (Stelling et al, 2002; Forster et al, 2003). Furthermore, networks provide, for example, a framework for the interpretation of synthetic lethal knockouts (Brummelkamp & Bernards, 2003; Sonoda et al, 2003). The analysis of intracellular network topology also provides an objective, genome-wide base for the classic idea that a cell can be divided into functional modules (Snel et al, 2002; Yanai & DeLisi, 2002; Davidson et al, 2003), and network topology correlates with sequence variation: sequences evolve slowly when they have many connections in the network (Fraser et al, 2002) or when they are part of relatively densely connected motifs (Wuchty et al, 2003). Finally, network approaches are used to integrate various types of genomics data to increase the reliability of predicted interactions (Jansen et al, 2003), and one can envision that the topology of intracellular networks provides constraints for the manipulation and design of cells.
The main source of data for the reconstruction of intracellular networks is genomics. Facets of the cellular network that have been studied include protein interaction networks in which the nodes (proteins) are connected when they physically interact (Uetz et al, 2000; Ito et al, 2001; Jeong et al, 2001; Wagner, 2001), metabolic networks in which the nodes (metabolites) are connected when they are substrates or products in the same biochemical reaction (Fell & Wagner, 2000; Jeong et al, 2000; Ma & Zeng, 2003), genomic association networks in which the nodes (genes) are connected when they occur repeatedly together in operons (Snel et al, 2002), and evolutionarily conserved coexpression networks (Stuart et al, 2003). The study of these networks has revealed that they all have a similar, nontrivial architecture. First, they are so-called scale-free networks. This means that there is no typical number of connections per node; rather the distribution of the number of connections (k) per node (N) follows a power law (N(k)∼k_−_γ). In other words, there are many nodes with few connections and a small but still significant number of nodes with many interactions. Second, these networks have a small-world architecture. This implies that, on the one hand, they are highly clustered: when a node is connected to two other nodes, the latter two also tend to have a direct connection to each other. On the other hand, the average shortest path length in the network (L, the minimum number of connections that one needs to get from one node to any other node) is almost as low as that for random networks (Watts & Strogatz, 1998). The scale-free, small-world architecture appears typical for intracellular networks in which the nodes are connected when they are involved in the same biological process. In contrast, another type of network, the gene regulatory network of Saccharomyces cerevisiae, in which the connections are between transcription factors and the genes they regulate, does not have a scale-free but rather an exponential distribution of the number of connections per node (Guelzim et al, 2002; Lee et al, 2002).
Because of the importance of molecular networks for the functioning of the cell, there is a great deal of interest in the evolution and origin of these networks. Yet it remains an open question whether the scale-free, small-world architecture is a direct product of selection and thus functionally meaningful, merely a by-product of the requirements of function and of selection at other levels, or even a natural consequence of mechanisms such as gene duplication. The evolution of scale-free networks has been explained in terms of selection on global properties such as robustness (Jeong et al, 2000; Guelzim et al, 2002) and the fast spread of perturbations (Fell & Wagner, 2000). It has also been addressed in phenomenological models (Bhan et al, 2002; Ravasz et al, 2002) that do not require selection but that are not supported by independent data. Here we analyse the network architecture of a general indicator of protein involvement in the same biological process: gene coexpression in S. cerevisiae (Hughes et al, 2000). We show that the gene coexpression network in S. cerevisiae is a scale-free, small-world network. By exploiting homology relations between the genes in the coexpression network, we formulate a neutralist model in which the scale-free, small-world architecture is a natural consequence of the mechanisms behind gene regulation evolution. This calls into question global selection mechanisms for the architecture of intracellular networks.
Results
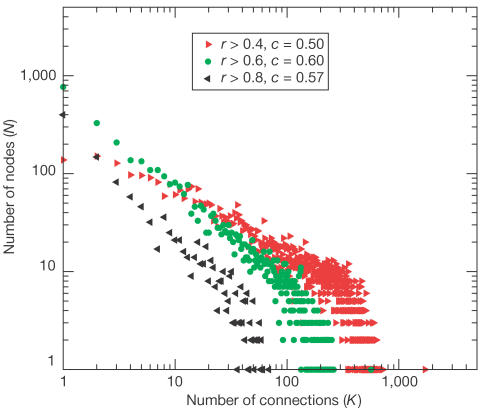
Although gene coexpression is a continuous observable, the underlying principle is discrete: the sharing of regulatory elements. We therefore translate gene coexpression into a discrete network. In the network, the genes are the nodes, which are connected to each other when coexpressed. Such a network representation allows a comparison of the global organization of gene expression with other facets of the intracellular network. Furthermore, relative to protein interaction networks or metabolic networks, coexpression covers a more inclusive array of functional relations between gene products. As a threshold to establish a link in the network between two genes, we chose a coexpression correlation of 0.6 in a large-scale expression data set (Hughes et al, 2000), as higher thresholds do not give higher reliabilities of functional interaction between the encoded proteins (van Noort et al, 2003). The coexpression network has 4,077 nodes (genes) that are linked by a total of 65,430 connections, the average number of connections per node (k) thus being 32 (each connection links two nodes). The distribution of number of links per node is scale free with degree exponent _γ_≈1 (Fig 1). Note that although the average number of connections is 32, most genes are connected to only one other gene, as reflected by the scale-free distribution (Fig 1). The clustering coefficient of the network (c, the fraction of cases where if a node has a connection to two other nodes, these two also have a direct connection to each other) is 0.6. Not all nodes are connected in one cluster; the largest cluster contains 3,945 nodes, with an average shortest path length (L) of 4. In a random network with the same number of nodes (N) and connections (k), _c_=0.008 (k/N) (Barabasi & Albert, 1999) and _L_≈2.8 (from simulations; see Methods). Thus, the yeast coexpression network has all the properties of a small-world (_L_≈_L_random, _c≫ c_random), scale-free (N(k)∼k_−_γ) network that is typical for intracellular networks in which the nodes are connected when they are involved in the same process. Using thresholds for coexpression higher than a correlation coefficient of 0.6 gave similar results, that is, a scale-free degree distribution and small-world organization (Fig 1). Using lower thresholds leads to the inclusion of ‘random' connections (van Noort et al, 2003) and an exponential degree distribution with a smaller c (Fig 1). At the threshold of 0.6, the network statistics are similar to previously studied biological networks (Fell & Wagner, 2000; Jeong et al, 2000, 2001; Wagner, 2001; Snel et al, 2002), and thus we use this network for further study.
Figure 1.
Distribution of connections per node in the coexpression network. Nodes are genes and connections are defined by coexpression of two genes, resulting in a network. The number of nodes (N) with a certain number of connections (k) in the coexpression network is shown, where coexpression is defined by a correlation in expression pattern higher than 0.4 (right-pointing arrows), 0.6 (circles) or 0.8 (left-pointing arrows). The distributions at thresholds 0.6 and 0.8 are scale free with an exponent _γ_≈1.
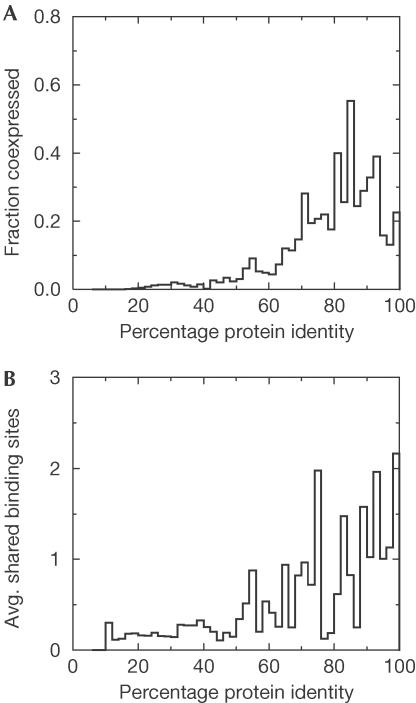
The coexpression data have another interesting property: a correlation between the fraction of coexpressed paralogues and their sequence similarity (Fig 2A). An independent data set that also contains this pattern is the large-scale, experimental determination of transcription factor binding sites (TFBSs) (Lee et al, 2002), in which the number of shared regulatory elements between paralogues increases with protein identity (Fig 2B). A correlation between divergence in sequence and in coexpression is expected if both diverge at constant, clock-like rates (Wagner, 2000), and indicates neutral evolution of these two traits. It appears that in the case of gene duplication, the regulatory elements tend to be coduplicated with the genes and mutated afterwards.
Figure 2.
Coexpression between paralogues in experiments. (A) Fractions of coexpressed paralogues calculated by correlation in coexpression in the data set of Hughes et al (2000). (B) Average number of shared regulatory elements between paralogues in the data set of Lee et al (2002).
Existing network-evolution models cannot account for the combination of the architecture of the coexpression network and the correlation between coexpression and sequence similarity in paralogues. The network model of Barabasi & Albert (1999), based on the concept of preferential attachment (Simon & Bonini, 1958), produces scale-free networks, but not small-world networks (_c_≈_c_random; in a small-world network _c≫c_random), even when introducing constraints to the number of connections per node or to the ageing of nodes (Amaral et al, 2000). The algorithm of Ravasz et al (2002) to realize a small-world, scale-free network involves hierarchical duplication of complete modules and attachment to the central node of the existing module. This model does not lead to a high likelihood of attachment between duplicated nodes, and is therefore not explanatory for the evolution of our network. Moreover, in contrast to the predictions of this model, the explicit testing of the age of genes (see Methods) and the number of their connections did not reveal any positive correlation (Pearson correlation=−0.04, _P_-value that there is no positive correlation=0.98). The duplication model of Bhan et al (2002) assumes duplication of genes with partial conservation of connections. When seeding this model with a scale-free network, most of the structure persists for a few iterations; however, simulating this model for a higher number of iterations results in an exponential degree distribution of N versus k (Pastorsatorras et al, 2003). In this model, there is no relation between the timing of a duplication event and the likelihood of attachment of the resulting paralogues. This is because the connections are fixed once established, as in all previous models. This is not an evolutionarily sound assumption, given the observation that connectivity between paralogues is dependent on the timing of the duplication event and that coexpression is only partly conserved between species (Teichmann & Babu, 2002; van Noort et al, 2003).
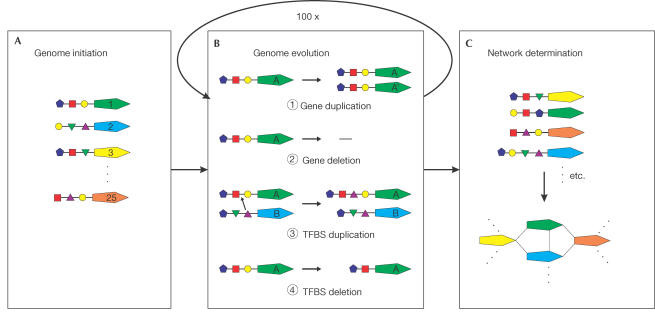
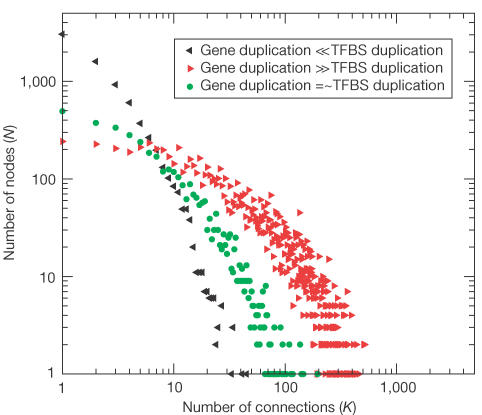
We introduce a new, simple model to explain the emergence of scale-free networks with a high clustering coefficient that is based on the observation of a positive correlation between the probability of a connection between two paralogues and their sequence similarity. In this model, the entities are genes that have a number of TFBSs. Connections between genes are established when they share a minimum number of TFBSs. At every time step, each gene has a probability of being duplicated, resulting in a new gene (step 1, Fig 3). In the case of duplication, the TFBSs are passed on to the duplicate gene, corresponding to a high likelihood of coexpression between recently duplicated paralogues in the experimental data. A gene may be deleted (step 2, Fig 3). A TFBS can be acquired from the pool of TFBSs of all genes, where the probability of obtaining a specific TFBS is proportional to its frequency in the genome (step 3, Fig 3), introducing connections between nonparalogous genes. New TFBSs are introduced at a low frequency. All TFBSs have a probability of being deleted (step 4, Fig 3), giving rise to a decrease in connectivity between duplicates over time and balancing the number of TFBSs per gene. We simulated this model by seeding it with 25 genes with randomly assigned TFBSs and evolving these for 100 evolutionary steps, observing three parameter regimes. In the first regime (left-pointing arrows, Fig 4), the TFBS duplication and deletion rates are much higher than the gene rates. This effectively decouples the TFBS from the genes and gives rise to a very loosely connected network (a steep slope), albeit with a power-law distribution of the number of connections per node and a high c (_c_=0.3 in this specific case). In the second regime (circles, Fig 4), the TFBS duplication and deletion rates are in the same order of magnitude as those for the genes. Here, we observe a scale-free degree distribution with a slope similar to the one observed in the experimental data and a high c. In the third regime (right-pointing arrows, Fig 4), the rates for TFBS duplication and deletion rates are much lower than those for genes. This couples the TFBS to the genes such that almost every pair of paralogues is connected, resulting in a very tightly connected network, with an exponentially declining degree distribution and a very high c (close to 1).
Figure 3.
Evolutionary model of transcription regulation. The evolutionary model consists of a few simple mechanisms. (A) A genome is initiated with 25 genes with random TFBSs, represented by the small coloured shapes. (B) Possible events are as follows: (1) Gene A is duplicated, gene A′ has the same TFBS as its duplicate gene A; the duplicates are coexpressed. (2) Gene deletion. (3) Gene A acquires a new TFBS from gene B. The probability of obtaining a specific TFBS is proportional to its frequency in the genome. The probability of a novel TFBS is (150 − total number of different TFBSs present)/(150+total number of TFBSs). (4) One of the TFBSs of gene A is deleted. (C) A network is constructed by connecting genes that share TFBSs.
Figure 4.
Distribution of connections per node in the simulated network. The number of nodes (N) with a certain number of connections (k) in the simulated network is shown. The minimum number of shared TFBSs for a connection in the network is three. Gene duplication and deletion are in the same order of magnitude as TFBS duplication and deletion (circles), gene duplication and deletion are much smaller than TFBS duplication and deletion (left-pointing arrows), and gene duplication and deletion are much larger than TFBS duplication and deletion (right-pointing arrows).
In a natural situation, we do not expect the evolutionary parameters to be in the third regime, as pieces of DNA are duplicated by the same mechanisms, be it coding or noncoding DNA. Also, TFBSs are much smaller than genes and are thus expected rather to have duplication and deletion rates that are at least as high as those for individual genes. A simulated network in the intermediary regime exists of, for example, 4,273 nodes connected by 56,953 connections. The network displays small-world behaviour, indicated by a high clustering coefficient (_c_=0.2) relative to random networks (_c_random=0.003) and in the largest cluster of 4,070 nodes an average shortest path length (_L_≈3) that is similar to the shortest path length in a random network (_L_random≈3.5). The overall behaviour of this network is very similar to the coexpression network. This indicates that a scale-free, small-world organization as such can be the result of neutral evolution. Still, the levels of cliquishness and the slope of the scale-free distribution may be the result of natural selection.
Discussion
The functional relevance of the typical scale-free, small-world organization that we observe in intracellular networks is open to debate. In the absence of an experimental system with which to test the functional relevance of the network architecture, we have to resort to theoretical experiments. These basically answer the following question: what are the minimal conditions under which a specific network architecture can evolve? To answer these questions, we have studied the coexpression network in S. cerevisiae that we show to have a small-world, scale-free architecture. Furthermore, the network contains a positive correlation between the probability of coexpression of two paralogues and their sequence similarity. We introduce a network model that reproduces the architecture as well as the homology relations in the coexpression network. Its key components are that genes are coduplicated with their TFBSs and that multiple shared TFBSs are required for coexpression. Our observation of a positive correlation between sequence similarity and the level of coexpression contrasts with the results of Wagner (2000), who only observed a very weak correlation. The difference is probably explained by the much larger coexpression data (Hughes et al, 2000) and the additional data set of TFBSs (Lee et al, 2002) combined with homology relations. This analysis of more data thus offers support for a neutralist's explanation of the gene coexpression network architecture.
In contrast, not only the scale-free, small-world architecture of intracellular networks but also one of the network statistics, the diameter, have been argued to be the result of biological selection. It should be noted that with respect to the diameter, the direction of this argument has been rather arbitrary: both the relatively small diameter of metabolic networks (Jeong et al, 2000) and the relatively large diameter of protein interaction networks (Maslov & Sneppen, 2002) have been argued to be the result of selection. Subsequent analyses have however shown that in both cases the networks were more random than proposed, and that the observed biases in the diameter size were either due to the choice of the network nodes (Ma & Zeng, 2003) or experimental bias in the underlying data set (Aloy & Russell, 2002). This leaves the argument that the scale-free, small-world architecture itself is a result of selection (Guelzim et al, 2002). As our model is purely mechanistic and the mechanisms are sufficient to explain the properties of the network, we do not need selection at the level of the network or at the level of gene regulation. This does not exclude the possibility of selection at that level or that the network architecture is in some way or another exploited by the cell, but it does call for a more sober view in interpreting network architectures in terms of selection and the benefits for the cell.
Methods
Random network. To evaluate the nontrivial properties of the coexpression network, it is compared with a random network. The random network is simulated by taking the same number of nodes as the coexpression network and randomly placing the same number of connections between these nodes.
Clustering coefficient and average shortest path length. The clustering coefficient (c) or the degree of cliquishness is computed by first counting all pairs of associations (cases where gene A is linked to gene B and to gene C), subsequently counting how often these pairs are closed (B is linked to C), and then dividing the second count by the first count (Watts & Strogatz, 1998). L is the average minimum number of nodes one needs to cross to get from one node to another. To obtain L, we compute the shortest path between all pairs of genes, and subsequently compute the average (Watts & Strogatz, 1998).
Gene age. The age of genes was determined by the amino-acid distance (100 – percentage protein identity) to the most distant paralogue (homologue within the same genome; Fitch, 1970). Duplications seem to be rampant in yeast; thus, when a gene was present very early in the genome, it is likely to have distant paralogues. This distance was then used to find out whether there is a correlation between gene age and the number of connections in the coexpression network.
Paralogues. To determine the correlation between protein identity and probability of connections between paralogues, we first need to determine paralogues. This is done by Smith–Waterman (Smith & Waterman, 1981) searches of the amino-acid sequences of the translated genes of S. cerevisiae (Goffeau et al, 1996) against each other. Matches with an _E_-value below 0.01 are considered paralogues.
Acknowledgments
This work was supported in part by a grant from the Netherlands Organization for Scientific Research (NWO).
References
- Aloy P, Russell RB ( 2002) Potential artefacts in protein-interaction networks. FEBS Lett 530: 253–254 [DOI] [PubMed] [Google Scholar]
- Amaral LA, Scala A, Barthelemy M, Stanley HE ( 2000) Classes of small-world networks. Proc Natl Acad Sci USA 97: 11149–11152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabasi AL, Albert R ( 1999) Emergence of scaling in random networks. Science 286: 509–512 [DOI] [PubMed] [Google Scholar]
- Bhan A, Galas DJ, Dewey TG ( 2002) A duplication growth model of gene expression networks. Bioinformatics 18: 1486–1493 [DOI] [PubMed] [Google Scholar]
- Brummelkamp TR, Bernards R ( 2003) New tools for functional mammalian cancer genetics. Nat Rev Cancer 3: 781–789 [DOI] [PubMed] [Google Scholar]
- Davidson EH, McClay DR, Hood L ( 2003) Regulatory gene networks and the properties of the developmental process. Proc Natl Acad Sci USA 100: 1475–1480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fell DA, Wagner A ( 2000) The small world of metabolism. Nat Biotechnol 18: 1121–1122 [DOI] [PubMed] [Google Scholar]
- Fitch WM ( 1970) Distinguishing homologous from analogous proteins. Syst Zool 19: 99–113 [PubMed] [Google Scholar]
- Forster J, Famili I, Palsson BO, Nielsen J ( 2003) Large-scale evaluation of in silico gene deletions in Saccharomyces cerevisiae. OMICS 7: 193–202 [DOI] [PubMed] [Google Scholar]
- Fraser HB, Hirsh AE, Steinmetz LM, Scharfe C, Feldman MW ( 2002) Evolutionary rate in the protein interaction network. Science 296: 750–752 [DOI] [PubMed] [Google Scholar]
- Goffeau A et al. ( 1996) Life with 6000 genes. Science 274: 546–567 [DOI] [PubMed] [Google Scholar]
- Guelzim N, Bottani S, Bourgine P, Kepes F ( 2002) Topological and causal structure of the yeast transcriptional regulatory network. Nat Genet 31: 60–63 [DOI] [PubMed] [Google Scholar]
- Hughes TR et al. ( 2000) Functional discovery via a compendium of expression profiles. Cell 102: 109–126 [DOI] [PubMed] [Google Scholar]
- Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y ( 2001) A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci USA 98: 4569–4574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen R, Yu H, Greenbaum D, Kluger Y, Krogan NJ, Chung S, Emili A, Snyder M, Greenblatt JF, Gerstein M ( 2003) A Bayesian networks approach for predicting protein–protein interactions from genomic data. Science 302: 449–453 [DOI] [PubMed] [Google Scholar]
- Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL ( 2000) The large-scale organization of metabolic networks. Nature 407: 651–654 [DOI] [PubMed] [Google Scholar]
- Jeong H, Mason SP, Barabasi AL, Oltvai ZN ( 2001) Lethality and centrality in protein networks. Nature 411: 41–42 [DOI] [PubMed] [Google Scholar]
- Lee TI et al. ( 2002) Transcriptional regulatory networks in Saccharomyces cerevisiae. Science 298: 799–804 [DOI] [PubMed] [Google Scholar]
- Ma H, Zeng AP ( 2003) Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics 19: 270–277 [DOI] [PubMed] [Google Scholar]
- Maslov S, Sneppen K ( 2002) Specificity and stability in topology of protein networks. Science 296: 910–913 [DOI] [PubMed] [Google Scholar]
- Pastor-Satorras R, Smith E, Sole RV ( 2003) Evolving protein interaction networks through gene duplication. J Theor Biol 222: 199–210 [DOI] [PubMed] [Google Scholar]
- Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabasi AL ( 2002) Hierarchical organization of modularity in metabolic networks. Science 297: 1551–1555 [DOI] [PubMed] [Google Scholar]
- Simon HA, Bonini CP ( 1958) The size distribution of business firms. Am Econ Rev 48: 607–617 [Google Scholar]
- Smith TF, Waterman MS ( 1981) Identification of common molecular subsequences. J Mol Biol 147: 195–197 [DOI] [PubMed] [Google Scholar]
- Snel B, Bork P, Huynen MA ( 2002) The identification of functional modules from the genomic association of genes. Proc Natl Acad Sci USA 99: 5890–5895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonoda E et al. ( 2003) Multiple roles of Rev3, the catalytic subunit of polzeta in maintaining genome stability in vertebrates. EMBO J 22: 3188–3197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J, Klamt S, Bettenbrock K, Schuster S, Gilles ED ( 2002) Metabolic network structure determines key aspects of functionality and regulation. Nature 420: 190–193 [DOI] [PubMed] [Google Scholar]
- Stuart JM, Segal E, Koller D, Kim SK ( 2003) A gene-coexpression network for global discovery of conserved genetic modules. Science 302: 249–255 [DOI] [PubMed] [Google Scholar]
- Teichmann S, Babu M ( 2002) Conservation of gene co-regulation in prokaryotes and eukaryotes. Trends Biotechnol 20: 407–410 [DOI] [PubMed] [Google Scholar]
- Uetz P et al. ( 2000) A comprehensive analysis of protein–protein interactions in Saccharomyces cerevisiae. Nature 403: 623–627 [DOI] [PubMed] [Google Scholar]
- van Noort V, Snel B, Huynen MA ( 2003) Predicting gene function by conserved co-expression. Trends Genet 19: 238–242 [DOI] [PubMed] [Google Scholar]
- Wagner A ( 2000) Decoupled evolution of coding region and mRNA expression patterns after gene duplication: implications for the neutralist–selectionist debate. Proc Natl Acad Sci USA 97: 6579–6584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A ( 2001) The yeast protein interaction network evolves rapidly and contains few redundant duplicate genes. Mol Biol Evol 18: 1283–1292 [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH ( 1998) Collective dynamics of ‘small-world' networks. Nature 393: 440–442 [DOI] [PubMed] [Google Scholar]
- Wuchty S, Oltvai ZN, Barabasi AL ( 2003) Evolutionary conservation of motif constituents in the yeast protein interaction network. Nat Genet 35: 176–179 [DOI] [PubMed] [Google Scholar]
- Yanai I, DeLisi C ( 2002) The society of genes: networks of functional links between genes from comparative genomics. Genome Biol 3, research0064 [DOI] [PMC free article] [PubMed] [Google Scholar]