Analysis of Binding Reactions by Fluorescence Recovery after Photobleaching (original) (raw)
Abstract
Fluorescence recovery after photobleaching (FRAP) is now widely used to investigate binding interactions in live cells. Although various idealized solutions have been identified for the reaction-diffusion equations that govern FRAP, there has been no comprehensive analysis or systematic approach to serve as a guide for extracting binding information from an arbitrary FRAP curve. Here we present a complete solution to the FRAP reaction-diffusion equations for either single or multiple independent binding interactions, and then relate our solution to the various idealized cases. This yields a coherent approach to extract binding information from FRAP data which we have applied to the question of transcription factor mobility in the nucleus. We show that within the nucleus, the glucocorticoid receptor is transiently bound to a single state, with each molecule binding on average 65 sites per second. This rapid sampling is likely to be important in finding a specific promoter target sequence. Further we show that this predominant binding state is not the nuclear matrix, as some studies have suggested. We illustrate how our analysis provides several self-consistency checks on a FRAP fit. We also define constraints on what can be estimated from FRAP data, show that diffusion should play a key role in many FRAP recoveries, and provide tools to test its contribution. Overall our approach establishes a more general framework to assess the role of diffusion, the number of binding states, and the binding constants underlying a FRAP recovery.
INTRODUCTION
The past few years have witnessed a dramatic increase in the application of fluorescence recovery after photobleaching (i.e., FRAP; reviewed in Meyvis et al., 1999; White and Stelzer, 1999; Reits and Neefjes, 2001; Houtsmuller and Vermeulen, 2001). Upon their development in the 70's, photobleaching techniques attracted a small cadre of biophysicists who utilized these methods primarily to determine diffusion constants of biomolecules in membranes (Liebman and Entine, 1974; Poo and Cone, 1974; Edidin et al., 1976; Schlessinger et al., 1976). Recently, with the advent of GFP fusion protein technology, the number of published FRAP experiments has skyrocketed. With this increase in FRAP studies has come an assortment of interpretations of FRAP data beyond measurement of diffusion constants. Indeed most recent FRAP experiments seek to infer something about how the GFP-tagged protein interacts with binding sites within the cell (e.g., McNally et al., 2000; Phair and Misteli, 2000). Toward this end, much of the current analysis is qualitative, assessing simply whether FRAP recovery curves are slower or faster after specific cellular perturbations (e.g., Dou et al., 2002). Faster or slower recoveries, respectively, are presumed to reflect weaker or tighter binding. In other cases, conclusions are drawn about the shape of a single recovery curve and how it may reflect underlying biological processes. For example, curves with a shoulder have been analyzed as containing fast and slow components that could correspond to diffusion and binding, or to two different binding states (Tardy et al., 1995; Kimura et al., 2002; Dundr et al., 2002; Carrero et al., 2003). More sophisticated quantitative analyses have also been performed to obtain rate constants for binding (Thompson et al., 1981; Kaufman and Jain, 1990; Berk et al., 1997; Bulinski et al., 2001; Coscoy et al., 2002; Dundr et al., 2002), although a number of these have examined regimes where the reaction dominates, presuming that diffusion can be safely ignored. Other attempts to simplify the full reaction-diffusion model have provided approximate solutions that allow the estimation of the binding rate constants but have yet to characterize the appropriateness of the assumptions made and the quality of the estimates (e.g., Carrero et al., 2003).
What is missing from this large compendium of experimental data and interpretive approaches is a comprehensive, analytical treatment of FRAP that provides a straightforward and consistent set of guidelines for how to analyze and interpret photobleaching data when binding interactions are present. This is a prerequisite if FRAP is to become a reliable and widely used approach to understanding and quantifying binding mechanisms within a cell. Various special cases of FRAP with binding have been considered previously, such as when diffusion dominates or when binding dominates (Kaufman and Jain, 1990, 1991; Bulinski et al., 2001), but the full spectrum of behaviors has not been characterized. The same system of equations that describes FRAP forms the theoretical basis of fluorescence correlation spectroscopy, where similar idealized models have also been utilized to determine binding rates (Elson and Magde, 1974; Elson, 1985, 2001). The connections among this disparate set of results are lacking, so no synthesis is available of all predicted FRAP recoveries in the presence of binding.
Here we present a detailed analysis of the simplest realistic case of binding that can be analyzed by FRAP, namely a single binding interaction in the presence of cellular diffusion, and also show how this can be extended to cases with multiple, independent binding interactions. Our goal is to provide a thorough, mathematically rigorous foundation for extracting binding information from FRAP recovery data. As such, we include an extensive Appendix describing in detail the mathematics underlying our analysis. In the main body of the text, we outline the key assumptions leading to the derivation of the FRAP model, and highlight the principal results and conclusions of our analysis.
As an example of the method's biological utility, we apply it to the problem of transcription factor mobility in the nucleus. In recent years, FRAP experiments have revealed that most nuclear proteins, including transcription factors, are highly mobile. Although transient binding interactions are presumed to influence the FRAP recovery of a transcription factor (Misteli, 2001), little is known about what these binding interactions are. Some evidence suggests that one class of transcription factors, the steroid hormone receptors, are bound to the nuclear matrix, an insoluble nuclear compartment devoid of DNA. These conclusions are derived from experiments in which either cellular ATP levels have been depleted (Stenoien et al., 2001) or proteasome activity has been inhibited (Stenoien et al., 2001; Deroo et al., 2002; Schaaf and Cidlowski, 2003) in cells containing GFP-tagged steroid hormone receptors. In either case, slower FRAP recoveries result, and extraction procedures demonstrate association of the steroid hormone receptor with the nuclear matrix (Tang and DeFranco, 1996). This has led to the suggestion that these receptors are normally bound to the nuclear matrix, and that their dissociation is promoted by energy and proteasome activity.
An alternative view is that these inhibition conditions induce an abnormal association with the nuclear matrix. Some investigators have suggested that the nuclear matrix is itself an artifact of the extraction conditions used to identify it (Pederson, 2000). An untreated cell examined by FRAP offers the opportunity to assess nuclear matrix binding without any perturbation of the system. More generally, it is of considerable interest to identify how many different binding states for a transcription factor are present in the nucleus of a normal cell and what the percent occupancy of each state is. This information is required as a starting point to understand nuclear mobility and its regulation. Mobility rate must play a key role in determining the search time required for a transcription factor to find its specific promoter amid a multitude of other binding sites in the nucleus.
Here we have applied our theory for FRAP recovery to nuclear mobility of a GFP-tagged glucocorticoid receptor (GFP-GR) in nuclei of both normal and ATP-depleted cells. Our results indicate that GFP-GR diffuses from one binding site to the next with an average time of ∼13 ms per binding event. Our analysis also suggests that in normal cells nuclear matrix binding at best accounts for a small fraction of bound GFP-GR with most GFP-GR molecules (∼90%) binding to a heretofore unidentified state.
More generally, our theoretical treatment provides several important insights for all biological FRAP analyses. First, we have defined constraints on what can be estimated from FRAP data. We show in several cases how the data enable evaluation only of the ratio of certain parameters, not their individual values. This is critical information for purely computational analyses, where such mathematical limitations may go unappreciated and lead to poor estimates of the individual parameters. Second, we have clarified the contribution of diffusion, binding, and the number of binding states to a FRAP recovery. We show that fast and slow components of a FRAP curve may sometimes represent weak and tight binding states, but that in many cases this is not true. Finally, we have found that diffusion will typically have to be incorporated in the analysis of many biological FRAP recoveries, even in very slow recoveries that last much longer than the recovery time for free diffusion. Ignoring this contribution will lead to erroneous conclusions.
METHODS
Cell lines
Mouse adenocarcinoma cell line 3617 was used for most experiments. The cells stably express GFP-GR under the control of a tetracycline-off system (Walker et al., 1999). For control experiments with GFP-only containing cells, the parental cell line (3134 cells) was transfected with a GFP plasmid (pEGFPC1, Clontech, Palo Alto, CA). Cells were grown and prepared for fluorescence imaging as previously described (Müller et al., 2001).
ATP depletion
The ATP-depletion conditions were similar to those used previously for GR (Tang and DeFranco, 1996), except adapted for microscopy. Cells were treated with 10 mM sodium azide (Sigma, St. Louis, MO) in glucose-minus-DMEM supplemented with 6 mM 2-deoxyglucose (Sigma) for 60 min and then brought to the microscope for FRAP experiments for up to 30 min longer.
Quantification of GFP-GR associated with the nuclear matrix
The nuclear matrix extraction procedure was similar to that previously described by Fey et al. (1986), adapted for visualization by fluorescence microscopy with a subsequent fixation step. Briefly, cells were treated with cytoskeleton buffer for 10 min at 4°C, extracted with 250 mM ammonium sulfate at 4°C for 5 min, and digested with DNase I for 30 min at room temperature. Cells were then fixed with 2% paraformaldehyde and examined by fluorescence microscopy on a Leica DMRA microscope (Leica, Exton, PA) equipped with a Photometrics Sensys charge-coupled device camera (Photometrics, Tucson, AZ) and images of nuclei recorded. Total nuclear fluorescence was measured with Metamorph software (Universal Imaging, Downingtown, PA).
FRAP protocol
FRAP experiments were performed on a Zeiss 510 confocal microscope (Carl Zeiss, Thornwood, NY) with either a 25×/0.8 NA dry objective for GFP-only cells, or a 100×/1.3 NA oil-immersion objective for GFP-GR cells. Cells were kept at 37°C using an air-stream stage incubator (Nevtek, Burnsville, VA). Bleaching was performed with a circular spot using the 488- and 514-nm lines from a 40-mW argon laser operating at 75% laser power. A single iteration was used for the bleach pulse, which lasted 0.8–40 ms depending on the bleach spot size. Fluorescence recovery was monitored at low laser intensity (0.2% of a 40-mW laser) at 0.8–40-ms intervals, depending on the experiment.
FRAP data manipulation
Approximately 10 separate FRAPs were performed and then averaged to generate a single FRAP curve. The temporal resolution was kept constant while measuring recovery, but this led to a very large number of closely spaced points in the second, slower phase of the recovery curve. To alleviate this, we averaged 10–30 adjacent points in this slower part of the curve. This generated roughly equally spaced points along the recovery curve and therefore avoided overly weighting the slower phase of the curve during fitting.
FRAP fitting
The model equations were programmed in Matlab (The Math Works, Natick, MA). The Matlab routine nlinfit was used to fit the models to experimental data. Using simulated FRAP curves, we found that nlinfit reliably converged to the correct fit for recoveries exhibiting either effective diffusion or reaction dominant behavior. In contrast, fits to simulated full model data often failed if the initial guess for one of the parameters was far from the true value. As a result, full model fits with real data were always performed by first sampling a grid of all possible 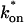 and _k_off values in 100.1 increments on a log scale to find the pair that yielded the smallest sum of residuals between the full model prediction and the experimental data. Then this (
and _k_off values in 100.1 increments on a log scale to find the pair that yielded the smallest sum of residuals between the full model prediction and the experimental data. Then this (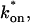 _k_off) pair was used as the initial guess in the nlinfit routine.
_k_off) pair was used as the initial guess in the nlinfit routine.
We reduced the number of fitted parameters in all full model fits by substituting a value for the free-diffusion constant _D_f. This value for GFP-GR (9.2 _μ_m2/s) was estimated from the measured value for GFP only (15.0 _μ_m2/s) by correcting for the additional mass of GR (94 kD for GR vs. 27 kD for GFP). Since _D_f _α M_−1/3, where M is mass, the predicted _D_f for GFP-GR is ∼60% of that for GFP alone.
Error analysis
We report all errors here as 95% confidence intervals. For all parameters estimated in the fit, the confidence intervals were directly produced by the nlinfit routine. Some of the estimates reported here depend not only on these fitted parameters, but also on the bleach spot size. Confidence intervals for the bleach spot size were determined from at least 10 measurements of the apparent spot size either in fixed cells for the smaller bleach spot, or in live cells for the larger bleach spots by measurement immediately (∼9 ms) after the bleach.
For pure or effective diffusion fits, the error in the bleach spot size could be directly incorporated into the final estimate using the formula for _τ_D (Eq. 8) or k*on/_k_off (Eq. 9) and the rules for convolution of errors. For full model fits, the bleach spot size enters as a term in the Laplace transform (Eq. 6), which is then inverted before fitting. Thus to estimate the impact of the bleach spot size error for full model fits, we produced estimates of k*on and _k_off using values for the bleach spot size at the endpoints of its 95% confidence interval. The resultant range in k*on and _k_off values was much larger than the 95% confidence interval computed by the nlinfit routine, an error based solely on the noise in the FRAP recovery data. Thus the error in the bleach spot size contributed more significantly, and so for this full model case, errors on k*on and _k_off values were taken as the endpoints produced from the bleach spot size errors.
MODEL
General equation: diffusion plus binding
We outline first the general equations underlying FRAP for a single binding reaction. Our nomenclature for the reaction is
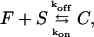 |
(1) |
|---|
where F represents free proteins, S represents vacant binding sites, C represents bound [FS] **c**omplexes, and _k_on and _k_off are the on- and off-rates, respectively. The equations for FRAP describing the preceding binding reaction must also incorporate diffusion. The most general case is a set of three coupled reaction-diffusion equations where f = [F], s = [S], and c = [C],
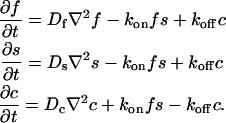 |
(2) |
|---|
Here ∇2 is the Laplacian operator and D represents the diffusion coefficient for each of the three species. The remaining terms reflect the standard chemical kinetics for the binding reaction in Eq. 1.
These equations can be simplified considerably by two assumptions that are applicable in many biological situations. The first simplifying assumption is that the biological system has reached equilibrium before photobleaching. For GFP fusion proteins, this means that the total amount of both GFP fusion protein and its binding sites remains constant over the time course of the fluorescence recovery. This is reasonable since most biological FRAPs recover on a timescale of seconds to several minutes, whereas GFP-fusion protein expression changes over a time course of hours, and is typically at a constant level by the time the FRAP experiment is performed. Therefore we assume equilibrium, and denote the corresponding equilibrium concentrations of F, S, and C by _F_eq, _S_eq, and _C_eq. Although the act of bleaching changes the number of visible free and complexed molecules (F or C), it does not change the number of free binding sites. Therefore _s = S_eq is a constant throughout the photobleaching recovery. This eliminates the second equation in Eq. 2, and also enables us to replace the variable s in the remaining two equations with a constant _S_eq. As a result, we can define a pseudo-first-order rate constant given by _k_on_S_eq = k*on. In what follows, we refer to this value as the pseudo-on rate.
The second simplifying assumption is that the binding sites are part of a large, relatively immobile complex, at least on the time- and length-scale of the FRAP measurement. This is a widely used approximation for FRAPs of, for example, either cytoskeletal or DNA binding proteins (Bulinski et al., 2001; Coscoy et al., 2002; Dundr et al., 2002). Ignoring diffusion of the bound complex results in _D_c = 0 in the expressions in Eq. 2.
With these two assumptions, the expressions in Eq. 2 reduce to
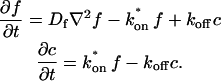 |
(3) |
|---|
Before the bleach, as noted above, the system is at equilibrium, and F and C have achieved steady-state values, _F_eq and _C_eq, so that the ratio of free/bound molecules is determined by
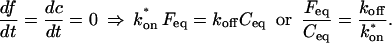 |
(4) |
|---|
Total equilibrium, as given above, is not altered by photobleaching, but the equilibrium for bleached and unbleached molecules is disturbed. Specifically, at the site of bleaching, the concentration of fluorescent molecules is significantly reduced, and so the return to equilibrium concentrations of fluorescence will be governed by the expressions in Eq. 3. Thus in what follows, f and c represent the concentration of fluorescent molecules after a photobleach that occurs at t = 0. The measured FRAP recovery data is the sum of free and bound fluorescence, averaged over the bleach spot: frap(t) = avg(f(t)) + avg(c(t)).
In what follows, we presume that the experimental data can be normalized such that the FRAP recovery ranges from 0 to 1. This normalization is acceptable if individual FRAP curves are analyzed one cell at a time. Typically, however, curves from multiple cells must be averaged to obtain smooth data, and in these circumstances care is required in pooling data. It is critical that cells of comparable fluorescent intensities be averaged if the data are subsequently normalized. Otherwise, different cells will have different levels of expressed fusion proteins, yielding different fractions of bound and free molecules in each cell. This in turn will lead to different FRAP recoveries if binding interactions are present, a feature that can in fact be exploited to obtain evidence for such interactions (Icenogle and Elson, 1983; Safranyos et al., 1987).
The final height of the FRAP recovery equals the sum of the equilibrium concentrations _F_eq _+ C_eq, and so normalization to 1 sets _F_eq _+ C_eq = 1 (which presumes that the bleach spot is small relative to the total cell volume, otherwise some measurable fraction of fluorescence will be lost after the bleach). Combining the preceding equality with Eq. 4 yields the following relationships for the equilibrium concentrations:
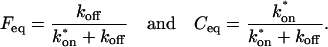 |
(5) |
|---|
We derive our solutions to the expressions in Eq. 3 for the case of a circular bleach spot. Circular bleach spots are now feasible and widely used in FRAP experiments performed on current scanning confocal microscopes. We also presume that there is a homogeneous distribution of fluorescence in the cell, and that the bleach spot is small relative to the size of the fluorescent compartment. Our model cannot be directly applied to rectangular bleach spots. Nor should it be applied to complicated cellular geometries such as endoplasmic reticulum, or to any highly heterogeneous distribution of fluorescence.
Finally, we adopt the convention of previous theoretical FRAP analyses and assume for simplicity two-dimensional diffusion in the plane of focus. This assumption is appropriate when the bleaching area forms a near-cylindrical shape through the cell, as occurs for a circular bleach spot of reasonable diameter. In this case, axial terms disappear from the Laplacian (∇2) in the expressions in Eq. 3 and only the radial component remains.
Analysis of the full reaction-diffusion equations
A strategy for obtaining a solution to the full reaction-diffusion system (Eq. 3) is to perform a Laplace transform. By analogy with the heat conduction problem between two concentric cylinders (Carslaw and Jaeger, 1959), a solution involving Bessel functions can be devised. Starting from the expressions in Eq. 3, we derive in the Appendix the general solution for the FRAP recovery within a circular bleach spot. We show there that the average of the Laplace transform of the fluorescent intensity within the bleach spot is given by
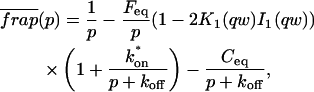 |
(6) |
|---|
where q depends on k*on, _k_off, and _D_f (see Eq. 15 in the Appendix), w is the radius of the bleach spot, _I_1 and _K_1 are modified Bessel functions of the first and second kind, and p is the Laplace variable that inverts to yield time. Thus the inverse transform of Eq. 6 can be computed numerically to yield the predicted FRAP recovery as a function of time. The numerical inversion requires ∼1 s with the Matlab routine invlap.m (Hollenbeck, 1998) running on a PC. This permits ready evaluation of how the predicted recovery depends on each of the parameters associated with the FRAP model.
This full model describes all possible behaviors of a FRAP recovery for a single binding reaction in the presence of diffusion. Therefore the model can be used to fit any FRAP recovery that involves a single binding reaction. In previous theoretical analyses of FRAP, three simplified cases of our full model solution have been considered. We refer to these as pure-diffusion dominant, effective diffusion, and reaction dominant behaviors. The pure-diffusion dominant solution is well understood and appreciated. The effective diffusion solution is also well understood, but virtually unknown in most of the FRAP community. The reaction dominant solution is not widely known, nor has it been completely developed. In what follows, we wish to determine when the full model is adequately described by one of these simplified scenarios. As a precursor, we explain each of these simplified scenarios and for each, either review or develop the complete solution for the FRAP recovery.
Pure-diffusion dominant
A first simplifying scenario arises when most of the fluorescent molecules are free. Under these conditions, FRAP measures primarily free diffusion of the fluorescently tagged molecule. For this free fraction, binding can be ignored and the expressions in Eq. 3 reduce to the diffusion equation,
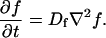 |
(7) |
|---|
The FRAP response for free diffusion has been extensively analyzed (Axelrod et al., 1976). For a circular bleach spot a closed form solution exists involving modified Bessel functions (Soumpasis, 1983) as
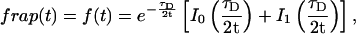
where
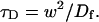 |
(8) |
|---|
Thus when binding is almost nonexistent and most molecules are free, the FRAP recovery curve should be fit by one parameter _τ_D in Eq. 8, thereby determining the diffusion constant _D_f.
Although solutions for the case of pure diffusion are well known, the relationship of the fitted diffusion constant to the molecular diffusion process underlying it is less clear. The complex geometry of cellular compartments and subcellular space influences the measured macroscopic diffusion constant (Feder et al., 1996; Siggia et al., 2000). For our purposes, the pure-diffusion constant measured by FRAP of a nonbinding protein, such as GFP unfused to a target protein, is sufficient to account for the contribution of diffusive processes in the FRAP recovery. Knowledge of this macroscopic diffusion behavior then enables us to extract the binding information contained in a FRAP recovery curve for a protein that both diffuses and binds.
Effective diffusion
The second simplified case for the expressions in Eq. 3 arises when the reaction process is much faster than diffusion. This implies that at any location within the bleach spot, the binding reaction rapidly achieves a local equilibrium. Under these conditions, Crank (1975) has shown that reaction-diffusion equations reduce to a simple diffusion equation but with a different diffusion constant, known as the effective diffusion constant, _D_eff. (Note the same term has been used by some authors to refer to diffusion in the cellular milieu—White and Stelzer, 1999; Siggia et al., 2000; Carrero et al., 2003—and this may or may not relate to the effective diffusion defined by Crank.) Here, we use the term effective diffusion to mean the slowed diffusion due to binding with
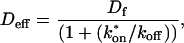 |
(9) |
|---|
where _D_f is the diffusion constant of the molecule in the absence of binding, and the off- and pseudo-on rates are as defined above. Note that the ratio of 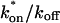 is the pseudo-equilibrium constant, which is the ratio of bound/free molecules (Eq. 4). _D_f can be determined by first measuring FRAP recoveries for GFP. The diffusion constant of the GFP fusion protein can then be calculated by allowing for its extra mass relative to GFP alone, and using the fact that, in the simplest scenario,
is the pseudo-equilibrium constant, which is the ratio of bound/free molecules (Eq. 4). _D_f can be determined by first measuring FRAP recoveries for GFP. The diffusion constant of the GFP fusion protein can then be calculated by allowing for its extra mass relative to GFP alone, and using the fact that, in the simplest scenario, 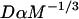 (see Methods). Thus, determination of _D_eff yields
(see Methods). Thus, determination of _D_eff yields 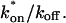
Since effective diffusion is governed by the standard diffusion equation, _D_eff can be determined by fitting the FRAP recovery curve with the diffusion model (Eq. 8). The fit will yield a value for _τ_D as
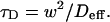 |
(10) |
|---|
This gives an estimate for _D_eff, and therefore the ratio 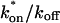 from Eq. 9. Note that the previous case, pure-diffusion dominant, is a subset of effective diffusion in which the binding is very weak, and so _D_eff = _D_f. For practical reasons, we have distinguished pure-diffusion dominant from effective diffusion because pure-diffusion dominant behavior provides no useable information about binding, whereas effective diffusion does.
from Eq. 9. Note that the previous case, pure-diffusion dominant, is a subset of effective diffusion in which the binding is very weak, and so _D_eff = _D_f. For practical reasons, we have distinguished pure-diffusion dominant from effective diffusion because pure-diffusion dominant behavior provides no useable information about binding, whereas effective diffusion does.
Reaction dominant
The third simplified scenario arises when diffusion is very fast compared both to binding and to the timescale of the FRAP measurement. Free molecules instantly equilibrate after the bleach, so that diffusion is not detected in the FRAP recovery. Unlike the pure and effective diffusion scenarios, a complete solution has not been developed for the case where the binding reaction dominates. Previously, Bulinski et al. (2001) demonstrated analytically that the rate constant for FRAP recovery is identical to the dissociation rate constant, _k_off. We have extended the analysis to enable the estimation of both k*on and _k_off from the FRAP recovery curve. As shown in detail in the Appendix, we find the following solution, which describes the total fluorescence recovery, f(t)+c(t), over time:
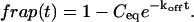 |
(11) |
|---|
_C_eq depends only on the off- and pseudo-on rates (Eq. 5), so the fit to the FRAP recovery in the reaction dominant case yields k*on and _k_off.
A surprising result of the preceding analysis is that the rate of FRAP recovery depends only on the off-rate. A similar result has been obtained in a less general context by Bulinski et al. (2001) and in a Fourier space analysis by Kaufman and Jain (1991). In all cases, the pseudo-on rate disappears from the exponential term for FRAP recovery because of the well-mixed assumption.
RESULTS OF SIMULATION AND MATHEMATICAL ANALYSIS
Evaluation of (k*on, _k_off) parameter space for the full reaction-diffusion equations
Given solutions for the full model and the three idealized cases of this model, we now investigate when these simplifications hold. Four parameters influence the solution to the general FRAP recovery as given by Eq. 6. These are the free diffusion constant (_D_f), the size of the bleach spot (w), the pseudo-on rate (k*on), and the off-rate (_k_off). Two of these four parameters are fairly similar from one laboratory to the next, namely the diffusion constant and the bleach spot size. Measured values for the cellular diffusion of free GFP range from ∼15–40 _μ_m2/s (Swaminathan et al., 1997; Arrio-Dupont et al., 2000; Coscoy et al., 2002), and in most FRAP experiments, the bleach spot size is on the order of 1 _μ_m in diameter. On the other hand, reported values for binding-association and binding-dissociation rate constants can vary over a much larger range (∼106-fold). Thus to investigate the range of behaviors exhibited by the full model (Eq. 6), we set the diffusion constant _D_f equal to 30 _μ_m2/s and the bleach spot radius to 0.5 _μ_m, and then varied the off- and pseudo-on rates over a 1010-fold range. Since _w_2/_D_f defines the timescale of the recovery, choosing particular values for w and _D_f does not prevent us from observing the entire range of behavior of this system.
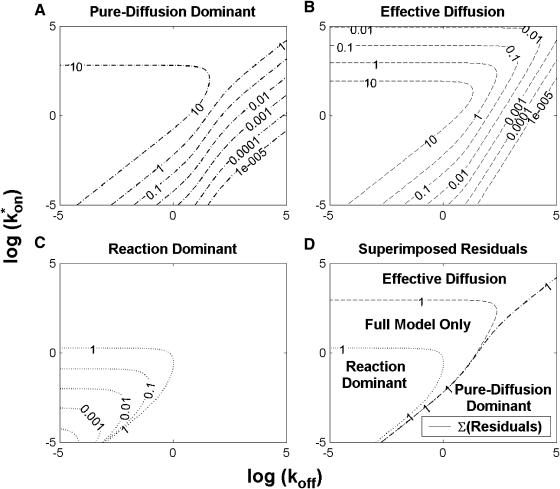
To identify values of the rate constants where the idealized cases hold (i.e., pure-diffusion dominant, effective diffusion, or reaction dominant), we used the full model to compute a FRAP recovery for a particular value of (k*on, _k_off). We then used each of the three idealized models to generate a predicted FRAP recovery curve by substituting (k*on, _k_off) into the equations for the idealized cases. The degree of fit between the full model and each idealized model was assessed. Depending on the particular values of (k*on, _k_off), four outcomes were obtained: The full model was well fit by both pure and effective diffusion (Fig. 1 A); or it was fit only by effective diffusion (Fig. 1 B); or it was fit only by reaction dominant (Fig. 1 C); or it was fit by none of these simplifications (Fig. 1 D). This indicates that for particular values of (k*on, _k_off) the idealized models can accurately predict the FRAP recovery of a single binding reaction.
FIGURE 1.
Model-predicted FRAP recovery curves. The FRAP recovery predicted by each idealized model is compared to that predicted by the full model (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m). Domains are identified where the full model is well fit by an idealized model (A–C), but this is not always the case (D). (A) With very weak binding, the pure-diffusion dominant model (red line) provides a good fit (sum of residuals = 0.08) to the full model (bold black line). Note that the effective diffusion model result is obscured by the pure-diffusion dominant curve and also provides a good fit; pure-diffusion dominant is a particular case of the effective diffusion model, namely _D_eff = _D_f. The reaction dominant model (orange line) provides a very poor fit. (B) With a high 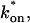 the effective diffusion model (green line) alone provides a reasonable fit to the full model (sum of residuals = 0.89). (C) With low
the effective diffusion model (green line) alone provides a reasonable fit to the full model (sum of residuals = 0.89). (C) With low 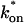 and low _k_off, the reaction dominant model (orange line) provides a good fit with the full model (sum of residuals = 0.66). (D) For certain values of
and low _k_off, the reaction dominant model (orange line) provides a good fit with the full model (sum of residuals = 0.66). (D) For certain values of 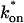 and _k_off, none of the idealized models result in a good fit to the full model (pure-diffusion dominant sum of residuals = 16.6; effective diffusion sum of residuals = 8.30; and reaction dominant sum of residuals = 8.54).
and _k_off, none of the idealized models result in a good fit to the full model (pure-diffusion dominant sum of residuals = 16.6; effective diffusion sum of residuals = 8.30; and reaction dominant sum of residuals = 8.54).
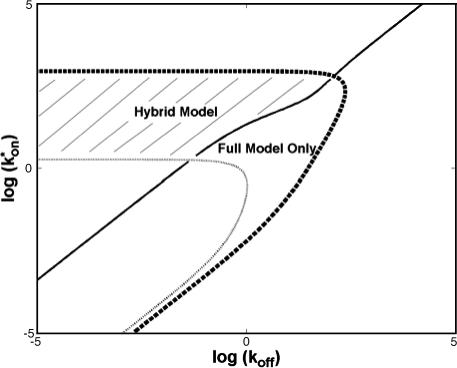
To determine the range of rate-constant values over which a particular idealized behavior was observed, we systematically varied k*on and _k_off and compared full model recoveries to recoveries for the idealized cases. Since we wanted to compare curves over the full range of the FRAP recovery, we first used the full model to determine the time required to reach 99% recovery for each (k*on, _k_off). The goodness of fit of each idealized case to the full model was quantified by computing the sum of residuals between the model curves at 200 equally spaced time points over the full range of recovery to 99%. For each comparison of the full model to an idealized model, a contour plot was constructed for the sum of residuals as a function of (k*on, _k_off) (Fig. 2, A–C). These contour plots define the shapes of the regions where the different idealizations hold. Larger residuals indicate progressively less accurate fits of the idealized models.
FIGURE 2.
Contour plots of model fits. For each idealized model, a contour plot of the sum of residuals between the idealized model and the full model demonstrates the degree of fit as a function of 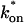 and _k_off (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m). (A) The pure-diffusion dominant model results in a good fit (i.e., the sum of residuals becomes small) as
and _k_off (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m). (A) The pure-diffusion dominant model results in a good fit (i.e., the sum of residuals becomes small) as 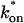 becomes small relative to _k_off (lower-right corner). (B) The effective diffusion model domain is made up of the pure-diffusion dominant regime plus the area with large values of
becomes small relative to _k_off (lower-right corner). (B) The effective diffusion model domain is made up of the pure-diffusion dominant regime plus the area with large values of 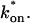 (C) The reaction dominant model matches the full model when both
(C) The reaction dominant model matches the full model when both 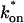 and _k_off are small (lower-left corner). (D) Superimposing the contour lines of the sum of residuals equal to 1 from parts A–C reveals the domains for each idealized model, as well as a region where none of the idealized models fit (full model only).
and _k_off are small (lower-left corner). (D) Superimposing the contour lines of the sum of residuals equal to 1 from parts A–C reveals the domains for each idealized model, as well as a region where none of the idealized models fit (full model only).
To define the boundary of each idealized domain, we estimated a threshold value for the sum of residuals at which the fits began to fail. By examining a number of fits like those in Fig. 1, we established a threshold of 1 for the sum of residuals beyond which the curves were obviously different. Superimposing the contour line corresponding to 1 from each of the three idealized cases (Fig. 2, A–C) produced a simplified map of the (k*on, _k_off) parameter space (Fig. 2 D).
We also characterized the rate-constant parameter space using two practical features easily assayed in FRAP experiments. These are the dependence on bleach spot size and the time required for full recovery. A dependence on bleach spot size is an experimental approach to assess whether diffusion contributes to the FRAP recovery. Using the full model we simulated this experiment by generating FRAP curves with the radius of the bleach spot set to either 1 _μ_m or 2 _μ_m. For the larger spot size, the time for 99% recovery was determined. Then over this time span, the recovery curves for the two spot sizes were calculated. The difference between the two curves was measured at 200 equally spaced time points, and the sum of the residuals plotted as a contour plot in (k*on, _k_off) parameter space (Fig. 3 A). The region with low residuals corresponds to the domain where the recovery is independent of bleach spot size, and therefore independent of diffusion. As expected, this region is the reaction dominant regime where diffusion is presumed to be so rapid that it can be neglected. Observe, however, that the majority of the rate-constant parameter space is dependent on bleach spot size. This shows that diffusion plays a role in most recoveries, at least in the absence of constraints on the values for the off- and pseudo-on rates.
FIGURE 3.
Practical observations from FRAP simulations. (A) A simulated test for bleach spot size dependence revealed a low sum of residuals between full model predictions when both 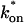 and _k_off were small (_D_f = 30 _μ_m2/s, _w_1 = 1 _μ_m, and _w_2 = 2 _μ_m). This corresponds well with the reaction dominant regime in Fig 2 D, the only domain independent of diffusion. (B) The contour plot shows the time (_t_99) predicted by the full model for FRAP recovery to 99% of original fluorescence (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m). The contour lines of the sum of residuals equal to 1 for the idealized models (Fig. 2 D; colored lines) are overlaid on top of the recovery times (black lines). Recovery times for typical FRAP experiments are generally between 1 and 1000 s, indicating that reaction dominant, effective diffusion, or full model behavior are all possible. (C) The boundaries between the idealized model domains can be approximated by three lines (see text; bold lines in figure), which are superimposed on the sum-of-residuals-equal-to-1 contour lines for each idealized model (_D_f = 30 _μ_m2/s and w = 0.5 _μ_m). (D) The precise locations of the idealized model domains are dependent upon the bleach spot size and cellular-diffusion constant of the fluorescently labeled protein. This contour plot shows how the idealized model domains shift as the bleach spot radius, w, and diffusion constant, _D_f, are changed (dash-dot line, _D_f = 35 _μ_m2/s, w = 0.4 _μ_m; solid line, _D_f = 30 _μ_m2/s, w = 0.5 _μ_m; and dashed line, _D_f = 25 _μ_m2/s, w = 0.6 _μ_m. The _w_2/_D_f values have units of s).
and _k_off were small (_D_f = 30 _μ_m2/s, _w_1 = 1 _μ_m, and _w_2 = 2 _μ_m). This corresponds well with the reaction dominant regime in Fig 2 D, the only domain independent of diffusion. (B) The contour plot shows the time (_t_99) predicted by the full model for FRAP recovery to 99% of original fluorescence (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m). The contour lines of the sum of residuals equal to 1 for the idealized models (Fig. 2 D; colored lines) are overlaid on top of the recovery times (black lines). Recovery times for typical FRAP experiments are generally between 1 and 1000 s, indicating that reaction dominant, effective diffusion, or full model behavior are all possible. (C) The boundaries between the idealized model domains can be approximated by three lines (see text; bold lines in figure), which are superimposed on the sum-of-residuals-equal-to-1 contour lines for each idealized model (_D_f = 30 _μ_m2/s and w = 0.5 _μ_m). (D) The precise locations of the idealized model domains are dependent upon the bleach spot size and cellular-diffusion constant of the fluorescently labeled protein. This contour plot shows how the idealized model domains shift as the bleach spot radius, w, and diffusion constant, _D_f, are changed (dash-dot line, _D_f = 35 _μ_m2/s, w = 0.4 _μ_m; solid line, _D_f = 30 _μ_m2/s, w = 0.5 _μ_m; and dashed line, _D_f = 25 _μ_m2/s, w = 0.6 _μ_m. The _w_2/_D_f values have units of s).
As a second practical result, we plotted the distribution of FRAP recovery times as a function of the off- and pseudo-on rates (Fig. 3 B). The recovery time was the time required for the full model to achieve 99% recovery. Typical FRAP recoveries studied experimentally vary anywhere from seconds to several minutes, and in a few cases up to several hours. These time ranges span the reaction dominant, full model, or effective diffusion domains, suggesting that any of these behaviors could be represented in actual FRAP experiments. Of particular practical interest is the fact that arbitrarily long recoveries exist in the full model and effective diffusion regimes. This is a counterintuitive result because diffusion by itself occurs on a much faster timescale, yet in these regimes diffusion contributes throughout the long recovery and cannot be ignored. Therefore a long recovery time is not sufficient grounds to accept a reaction dominant model.
The contour plot of recovery times (Fig. 3 B) also provides some additional insights into the three idealized domains of pure-diffusion dominant, effective diffusion, and reaction dominant. The pure-diffusion dominant regime corresponds approximately to the domain with recovery times of <1 s. In this case binding is so weak that it does not slow down the FRAP recovery. The effective diffusion regime corresponds approximately to the region where the contour lines for recovery times are parallel with slope equal to 1. This follows from the fact that the effective diffusion constant depends only on the ratio of k*on/_k_off (see Eq. 9), so constant values of this ratio yield the same recovery time. This generates a family of lines with slope 1 in the log/log rate-constant parameter space. Finally the reaction dominant domain corresponds approximately to the region where the contour lines for recovery times are parallel and vertical. Here the reaction dominant idealization results in a FRAP recovery rate that depends only on the off-rate (Eq. 11), so for constant _k_off, the recovery time is the same.
A simplified view of rate-constant parameter space
The basic geometry of the rate-constant parameter space determined above can be explained with a few rules. The boundaries dividing the four separate regions of parameter space can be approximated by three lines (Fig. 3 C). The pure-diffusion dominant regime occurs when the ratio of bound to free molecules is ∼1% or less. From Eq. 4, 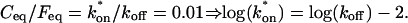 Hence the border of the pure-diffusion dominant regime in log/log parameter space is approximated by a line of slope 1 and _y_-intercept of −2 (red line in Fig. 3 C). As noted above, the pure-diffusion dominant regime is actually a subdomain of effective diffusion. Therefore the practical effective diffusion regime is bounded on the right by the pure-diffusion dominant regime, and approximately defined by the remaining region above the line log (k*on) = 3 (green line in Fig. 3 C). Similarly, the reaction dominant regime is bounded below by the pure-diffusion dominant regime, and approximately defined by the remaining region below the line log (k*on) = 0 (orange line in Fig. 3 C). The remaining domain requires the full model (Eq. 6). The exact location of the boundaries between these regimes is dependent upon the applicable values of w and _D_f (Fig. 3 D).
Hence the border of the pure-diffusion dominant regime in log/log parameter space is approximated by a line of slope 1 and _y_-intercept of −2 (red line in Fig. 3 C). As noted above, the pure-diffusion dominant regime is actually a subdomain of effective diffusion. Therefore the practical effective diffusion regime is bounded on the right by the pure-diffusion dominant regime, and approximately defined by the remaining region above the line log (k*on) = 3 (green line in Fig. 3 C). Similarly, the reaction dominant regime is bounded below by the pure-diffusion dominant regime, and approximately defined by the remaining region below the line log (k*on) = 0 (orange line in Fig. 3 C). The remaining domain requires the full model (Eq. 6). The exact location of the boundaries between these regimes is dependent upon the applicable values of w and _D_f (Fig. 3 D).
These boundaries as defined empirically clarify apparently conflicting theoretical approximations of reaction-diffusion equations reported in the literature. Crank (1975) concludes that boundaries between different regimes depend on the magnitude of _k_off. Kaufman and Jain (1990) assert that the boundaries depend on the magnitude of k*on. Elson and co-workers conclude that the sum of k*on + _k_off is critical (Elson and Magde, 1974; Elson and Reidler, 1979). All of these constraints can be applied to explain subregimes of our rate-constant parameter space, but they cannot account for the complete parameter space. Rather our rules detailed above provide the simplest explanation, namely that for a large free pool (_C_eq/_F_eq ≤ 0.01), pure diffusion dominates, otherwise the magnitude of k*on partitions the remainder of the space into reaction dominant, full model, or effective diffusion.
To confirm these empirical observations, we show mathematically in the Appendix that our full model solution reduces to each of the idealized cases by applying the constraints outlined in Fig. 3 C. Namely, the full model (Eq. 6) simplifies to:
- The pure-diffusion dominant model (Eq. 8) when the free pool is large
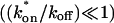 ;
; - The effective-diffusion model (Eqs. 8–10) when the pseudo-on rate is large compared to the characteristic diffusion time
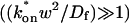 ; and
; and - The reaction-dominant model (Eq. 11) when the pseudo-on rate is small compared to the characteristic diffusion time
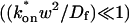 and _C_eq is significantly large
and _C_eq is significantly large 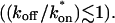
See Derivation of Idealized Solutions from the Full Model in the Appendix for the derivations.
In the Appendix, we also examine mathematically the transition between the pure-diffusion dominant regime and the reaction dominant regime, as well as the transition between the reaction dominant regime and the effective diffusion regime. The crossover from pure-diffusion dominant to reaction dominant occurs in the lower half of the plot in Fig. 3 C, namely for 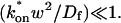 With this constraint, we show in the Appendix that the full model solution can be simplified to the sum of two terms, one representing the pure-diffusion component, multiplied by the size of the free pool, plus a second representing the reaction component, multiplied by the size of the bound pool (see Eq. 41 and its derivation in the Appendix). Thus in this domain of (k*on, _k_off) parameter space, the FRAP recovery curve is always the sum of two independent processes, diffusion plus reaction, each of which contributes to the total recovery based on both the size of the free and bound pools and on the characteristic times for recovery _w_2/_D_f and 1/_k_off. Typically, one process dominates, and this leads to the zones we have called either pure-diffusion dominant or reaction dominant. We see a sharp transition between these zones in Fig. 3 C because we used 99% recovery as an arbitrary threshold for full recovery. When the free pool falls below 99%, then the bound pool with its typically much slower recovery timescale of 1/_k_off becomes a significant component of the recovery to 99% of final fluorescence. As a result, recovery times slow suddenly upon crossover to the reaction dominant regime.
With this constraint, we show in the Appendix that the full model solution can be simplified to the sum of two terms, one representing the pure-diffusion component, multiplied by the size of the free pool, plus a second representing the reaction component, multiplied by the size of the bound pool (see Eq. 41 and its derivation in the Appendix). Thus in this domain of (k*on, _k_off) parameter space, the FRAP recovery curve is always the sum of two independent processes, diffusion plus reaction, each of which contributes to the total recovery based on both the size of the free and bound pools and on the characteristic times for recovery _w_2/_D_f and 1/_k_off. Typically, one process dominates, and this leads to the zones we have called either pure-diffusion dominant or reaction dominant. We see a sharp transition between these zones in Fig. 3 C because we used 99% recovery as an arbitrary threshold for full recovery. When the free pool falls below 99%, then the bound pool with its typically much slower recovery timescale of 1/_k_off becomes a significant component of the recovery to 99% of final fluorescence. As a result, recovery times slow suddenly upon crossover to the reaction dominant regime.
The crossover from reaction dominant to effective diffusion occurs in the left half of the plot of Fig. 3 C, where 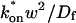 goes from small to large. This transition is also analyzed mathematically in the Appendix. A simplified solution can be obtained when the free fraction, _F_eq, is small (
goes from small to large. This transition is also analyzed mathematically in the Appendix. A simplified solution can be obtained when the free fraction, _F_eq, is small (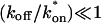 ). This leads to a reduced model equation which depends on only two parameters, _k_off and the ratio
). This leads to a reduced model equation which depends on only two parameters, _k_off and the ratio 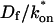 (Eq. 43). We call this the hybrid model and show in the Appendix that it involves a somewhat complicated combination of reaction-like and diffusion-like terms (Eq. 46). Thus in this regime, reaction and diffusion are coupled and not separable. For large
(Eq. 43). We call this the hybrid model and show in the Appendix that it involves a somewhat complicated combination of reaction-like and diffusion-like terms (Eq. 46). Thus in this regime, reaction and diffusion are coupled and not separable. For large 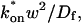 the hybrid model reduces to effective diffusion, whereas for small
the hybrid model reduces to effective diffusion, whereas for small 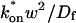 it reduces to reaction dominant (see Appendix). The significance of this hybrid model is that it occupies a large portion of our full model domain (see Fig. 8 in Appendix), and therefore in this region the full model is capable of predicting only the ratio
it reduces to reaction dominant (see Appendix). The significance of this hybrid model is that it occupies a large portion of our full model domain (see Fig. 8 in Appendix), and therefore in this region the full model is capable of predicting only the ratio 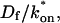 rather than unique values for each parameter. Additionally, the complex combination of reaction and diffusion terms in the hybrid model solution indicates that in this regime, it is inappropriate to expect or assign fast and slow components to the FRAP recovery, as is often attempted in the analysis of FRAP results (Kimura et al., 2002). Rather, it should be recognized that both the hybrid model (Eq. 46) and the effective diffusion solution (Eqs. 8–10) may appear by eye to contain two separate recovery phases, despite the fact that they cannot be separated into discrete reaction and diffusion processes.
rather than unique values for each parameter. Additionally, the complex combination of reaction and diffusion terms in the hybrid model solution indicates that in this regime, it is inappropriate to expect or assign fast and slow components to the FRAP recovery, as is often attempted in the analysis of FRAP results (Kimura et al., 2002). Rather, it should be recognized that both the hybrid model (Eq. 46) and the effective diffusion solution (Eqs. 8–10) may appear by eye to contain two separate recovery phases, despite the fact that they cannot be separated into discrete reaction and diffusion processes.
Extension to two (or more) independent binding states
Many biological binding interactions involve more than a single binding state. Thus it is of interest to generalize the preceding findings. In the Appendix, we develop the full model Laplace transform solution for two independent binding states, and also derive closed form solutions for each of the three idealized cases (pure-diffusion dominant, effective diffusion, reaction dominant) for two independent binding states. The resultant equations are natural extensions of the one-binding-state model, and it is therefore clear how to extend them further to three or more independent binding states. Thus our analysis presented in the Appendix provides a guide for how complete solutions can be obtained for an arbitrary number of independent binding states.
Based on these model equations, we have performed a detailed analysis of the two-binding-state system. As detailed in the Appendix, we show that the same three idealized cases are still good approximations to the full model under certain conditions. This means in particular that in the presence of significant binding interactions, either the two-state effective diffusion model or the two-state reaction dominant model will provide excellent fits for some FRAP recoveries. Thus the model equations we derive for these scenarios will find practical application. We also show once again that there is a domain in rate-constant parameter space in which only the full model solution is valid, and so our complete Laplace transform solution for two binding states will also find practical application.
By an extensive exploration of rate-constant parameter space for the two-binding-state model, we find that the full model domain is larger compared to the one-state model (see discussion in the Appendix). The increase in size of the full model domain occurs at the expense of the reaction dominant and effective diffusion domains. We show that these regions shrink because full model behavior typically results whenever binding reactions from different regimes are combined (Fig. 4). For example, if one binding state has rate constants characteristic of effective diffusion (for the one-state model), and the other state has rate constants characteristic of reaction dominant (for the one-state model), the combination will typically produce full model behavior for the two-state model. As this is generally true for any combination of reactions drawn from different regimes, the full model regime becomes progressively larger as the number of binding states increases.
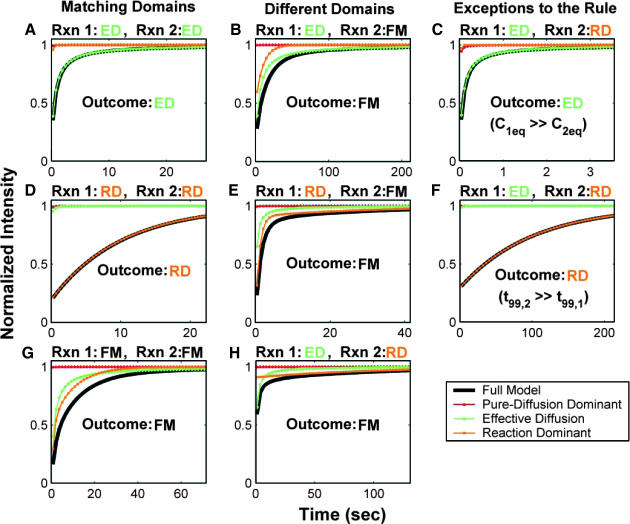
FIGURE 4.
Model-predicted FRAP recovery curves for two binding reactions. (A, D, and G) Matching domains: When both individual reactions exhibit the same idealized behavior, then the FRAP recovery predicted by the two-reaction full model (bold black line) is fit by the two-reaction model of that idealized behavior (colored lines). For example in A, given that 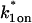 and _k_1off place one reaction in the single-reaction effective diffusion domain, and that
and _k_1off place one reaction in the single-reaction effective diffusion domain, and that 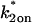 and _k_2off place the other reaction in the single-reaction effective diffusion domain, the two-reaction full model FRAP recovery is well fit by the two-reaction effective diffusion model (see Eq. 59). (B, E, and H) Different domains: When the individual reactions do not exhibit the same idealized behavior, then none of the two-reaction idealized models will match the FRAP recovery predicted by the full two-reaction model. In this case, the full two-reaction model is required (Eq. 55). (C and F) Exceptions to the rule: When either the equilibrium concentration or the time for recovery is much greater for one of the reactions than the other, then the two-reaction full model result will be fit by the two-reaction idealized model of the reaction with the larger concentration or longer time. (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m. ED, effective diffusion model; RD, reaction dominant model; and FM, full model.)
and _k_2off place the other reaction in the single-reaction effective diffusion domain, the two-reaction full model FRAP recovery is well fit by the two-reaction effective diffusion model (see Eq. 59). (B, E, and H) Different domains: When the individual reactions do not exhibit the same idealized behavior, then none of the two-reaction idealized models will match the FRAP recovery predicted by the full two-reaction model. In this case, the full two-reaction model is required (Eq. 55). (C and F) Exceptions to the rule: When either the equilibrium concentration or the time for recovery is much greater for one of the reactions than the other, then the two-reaction full model result will be fit by the two-reaction idealized model of the reaction with the larger concentration or longer time. (_D_f = 30 _μ_m2/s, w = 0.5 _μ_m. ED, effective diffusion model; RD, reaction dominant model; and FM, full model.)
The significance of a larger full model domain is that the complete Laplace transform solution will be required more often as the number of binding states increases. In addition, since the full model domain incorporates diffusion, the likelihood that diffusion is required for fitting the FRAP recovery increases with the number of binding states.
Expected FRAP behaviors
Given the description of rate-constant parameter space for the one-binding-state model (Fig. 3 C), and the rules described above and in the Appendix for the two- (or more) binding-state models, it is of interest to estimate which types of behavior typical biological FRAPs should exhibit. In the absence of binding interactions, the FRAP recovery of the fusion protein reflects the pure-diffusion scenario, with a recovery rate very similar to that of GFP alone (differing only in proportion to the added mass of the fusion protein). In cases where significant differences exist between the recovery of the fusion protein and GFP alone, binding interactions are implicated. Considering typical ranges for the binding rate constants provides some feel for the likelihood of possible FRAP outcomes. Typical off-rates range from ∼101 s−1 for nonspecific DNA binding to ∼10−6 s−1 for many types of specific binding. Thus most biological FRAPs should occupy the left half of Fig. 3 C where reaction dominant, full model, or effective diffusion should occur.
To see which of these behaviors are possible or likely, on-rates must be considered. The diffusion-limited on-rate is ∼106 M−1 s−1, although this is not an absolute upper bound. Typical on-rates range from 102–108 M−1 s−1. It is the pseudo-on rate, namely the product of the on-rate with the equilibrium concentration of bound sites, that determines location in the rate-constant parameter space of Fig. 3 C. Thus for diffusion-limited on-rates (∼106 M−1 s−1), a 1-mM concentration of bound sites will yield pseudo-on rates of ∼103 s−1 or effective diffusion behavior, whereas a 1-_μ_M concentration of bound sites will yield pseudo-on rates of 100 s−1 near the boundary between the full model and reaction dominant. Thus the reaction dominant regime can be entered by a combination of slower on-rates and low concentrations of binding sites. Considering a specific case, DNA binding in a mammalian nucleus of ∼5-_μ_m radius and 6 × 109 basepairs of DNA, the concentration of basepair sites is ∼20 mM. Others have estimated the concentration of DNA in the nucleus as high as ∼100 mM (Lieberman and Nordeen, 1997). In this latter case, the smallest possible value for k*on is 101 s−1, altogether eliminating reaction-dominant as a possible behavior. However, this value for DNA concentration is probably an upper limit, since the number of available sites might well be reduced by constraints that limit access to some subset of sites. Nevertheless, these rough calculations suggest that many FRAPs should exhibit behavior that depends on diffusion either via the full model or effective diffusion. This is underscored by the analysis of models with two or more binding states which indicate that the domain occupied by the full model increases (see the preceding section). In sum, reaction dominant, effective diffusion, and full model behavior are all possible outcomes of FRAP experiments, but the latter two behaviors with their dependence on diffusion should be more common than currently appreciated.
EXPERIMENTAL RESULTS AND DISCUSSION
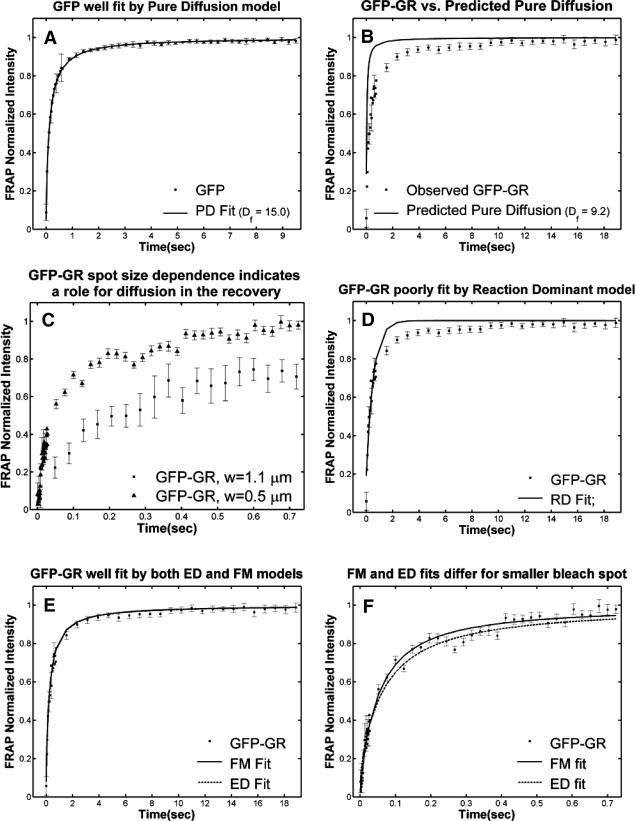
To test the utility of the preceding theoretical development, we applied the method to the problem of transcription factor mobility. We first evaluated our experimental protocol for FRAP using mouse adenocarcinoma cells transfected with GFP only. The average recovery was well fit by Eq. 8 for pure-diffusion dominant behavior (Fig. 5 A) yielding a cellular diffusion constant _D_f for GFP of 15.0 _μ_m2/s, within the range observed in other studies (Swaminathan et al., 1997; Arrio-Dupont et al., 2000; Coscoy et al., 2002). The good fit and accurate determination of _D_f demonstrate that our FRAP protocol satisfies the basic assumptions of our model.
FIGURE 5.
Control GFP-GR results. (A) The FRAP recovery of GFP (▪, n = 12) is well fit by the pure-diffusion dominant model (solid line), with _D_f = 15.0 _μ_m2/s (w = 2.7 _μ_m). In this and all other figures, the error bars represent the 95% confidence interval of each data point. For clarity not all error bars are shown for early time points. (B) The pure-diffusion dominant model (solid line) was simulated using Eq. 8 with w = 1.1 _μ_m and _D_f = 9.2 _μ_m2/s, which is the predicted diffusion constant for GFP-GR in the nucleus based on the measured diffusion constant for GFP and the size difference between GFP and GFP-GR. The observed FRAP recovery of GFP-GR (▪, n = 10) was significantly slower, indicating the presence of binding interactions. (C) FRAP of GFP-GR with different bleach spot sizes reveals a dependence on spot size and, therefore, diffusion (n = 10 in each case). (D) Consistent with the dependence on spot size and diffusion, the reaction dominant idealized model (solid line) provides a poor fit to the GFP-GR FRAP recovery (w = 1.1 _μ_m). (E) The FRAP recovery of GFP-GR (w = 1.1 _μ_m) is well fit by the effective diffusion model (dashed line, obscured by FM fit curve), with _D_eff = 1.3 _μ_m2/s. This yields an estimate of the pseudo-equilibrium constant, 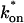 /_k_off = 6.0, via Eq. 9, with _D_f = 9.2 _μ_m2/s. The full model (solid line) also provides a good fit to the data, with a similar value of the pseudo-equilibrium constant (
/_k_off = 6.0, via Eq. 9, with _D_f = 9.2 _μ_m2/s. The full model (solid line) also provides a good fit to the data, with a similar value of the pseudo-equilibrium constant (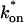 /_k_off = 5.8) calculated from the full model estimates of
/_k_off = 5.8) calculated from the full model estimates of 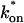 = 500 s−1 and _k_off = 86.4 s−1. (F) With the bleach spot size reduced to 0.5 _μ_m, the effective diffusion (dashed line) and full model (solid line) provide reasonably good fits. However, the full model fit yields a clear improvement in the sum of residuals (see Table 1), in contrast to the larger-spot-size experiment where the sum of residuals does not change appreciably between the effective diffusion and full model fits (see Table 1 and E). The smaller spot size has therefore moved the FRAP recovery to the boundary between effective diffusion and the full model, enabling independent estimates of
= 500 s−1 and _k_off = 86.4 s−1. (F) With the bleach spot size reduced to 0.5 _μ_m, the effective diffusion (dashed line) and full model (solid line) provide reasonably good fits. However, the full model fit yields a clear improvement in the sum of residuals (see Table 1), in contrast to the larger-spot-size experiment where the sum of residuals does not change appreciably between the effective diffusion and full model fits (see Table 1 and E). The smaller spot size has therefore moved the FRAP recovery to the boundary between effective diffusion and the full model, enabling independent estimates of 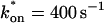 and _k_off = 78.6 s−1. These estimates yield
and _k_off = 78.6 s−1. These estimates yield 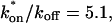 which is in reasonable agreement with that found in the larger-spot-size experiment shown in E.
which is in reasonable agreement with that found in the larger-spot-size experiment shown in E.
We next performed FRAPs of a GFP-tagged glucocorticoid receptor within nuclei of mouse adenocarcinoma cells. This cell line contains a stably expressed GFP-GR yielding rather similar expression levels from cell to cell. To enable valid normalization of data, cells of comparable intensity were selected for all photobleaching experiments. Within each nucleus, the distribution of GFP-GR is also rather uniform, except within nucleoli where it is largely absent (see Fig. 7 A). To reduce boundary effects from nucleoli or the nuclear membrane, FRAP measurements of GFP-GR were at sites as far away from these structures as feasible. This satisfies the requirements of our model for a homogeneous distribution of fluorescence without complex cellular geometries.
FIGURE 7.
Nuclear matrix extraction. (A) Before the nuclear matrix extraction procedure, cell nuclei appear bright with GFP-GR fluorescence. (B) In control cells almost all fluorescence disappears after nuclear matrix extraction. (C) In cells treated with sodium azide the nuclei retain a large amount of fluorescence after nuclear matrix extraction, indicating that GFP-GR is immobilized at the matrix under these conditions. Bar = 10 _μ_m. (D) The amount of fluorescence lost after nuclear matrix extraction was quantified. In control cells 5% of fluorescence is retained (n = 99), whereas in azide-treated cells 40% of fluorescence is retained (n = 86). The large amount of fluorescence retained at the nuclear matrix in azide-treated cells matches the two-state full model prediction that 44% of GFP-GR in the nucleus is bound in a second reaction state.
We first performed FRAPs of GFP-GR using a 1.1-_μ_m-radius circular bleach spot, and asked which of the four regimes (see Fig. 3 C) best described the recovery. The pure-diffusion regime was eliminated because the GFP-GR recovery was significantly slower than the prediction for pure diffusion (Fig. 5 B) based on the expected mass of GFP-GR (see Methods). This indicates the presence of binding interactions. To determine if the recovery was in the reaction dominant regime, cell nuclei were bleached with two different bleach spot sizes, and significantly different recoveries were detected (Fig. 5 C). This indicates that diffusion contributes measurably to the GFP-GR recovery, and eliminates the reaction dominant regime where no dependence on bleach spot size should be observed (see Fig. 3 A). Consistent with this, the recovery was poorly fit with a single-binding-state reaction dominant model (Fig. 5 D). Together these results rule out reaction dominant behavior for the GFP-GR recovery, and implicate one of the diffusion-dependent models, namely effective diffusion or the full model.
Both effective diffusion and the full model yielded good, mutually consistent fits (Fig. 5 E). The full model fit predicted rate constants k*on = 500 s−1 and _k_off = 86.4 s−1. As a consistency check, we determined in which regime these rate constants were located (see Fig. 3 C). This was done by using the predicted 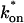 from the full model fit to calculate
from the full model fit to calculate 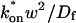 (see the rules defining domains in Fig. 3 D). The computed value of 65 was ≫1, thereby placing the full model fit in the effective diffusion regime. Since the full model encompasses all simplified regimes, we expect it to agree with the effective diffusion model when this simplified scenario holds. As further proof of self consistency, we found that the predicted rate constants from the full model yielded a ratio of
(see the rules defining domains in Fig. 3 D). The computed value of 65 was ≫1, thereby placing the full model fit in the effective diffusion regime. Since the full model encompasses all simplified regimes, we expect it to agree with the effective diffusion model when this simplified scenario holds. As further proof of self consistency, we found that the predicted rate constants from the full model yielded a ratio of 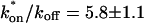 which was similar to that predicted directly from the effective diffusion fit, namely
which was similar to that predicted directly from the effective diffusion fit, namely 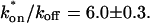 Thus we conclude that the GFP-GR FRAP recovery exhibits effective diffusion when the spot size radius is 1.1 _μ_m.
Thus we conclude that the GFP-GR FRAP recovery exhibits effective diffusion when the spot size radius is 1.1 _μ_m.
As Eqs. 9 and 59 show, the same effective diffusion fit may represent one or several different binding states. To assess the number of GFP-GR binding states, we attempted to shift the FRAP recovery from the effective diffusion regime to the full model regime, where the number of binding states can be directly determined. Regime boundaries (Fig. 3 D) are inversely proportional to _w_2/D. Therefore a sufficiently small bleach spot size (w) should shift the boundary for the full model upward such that it eventually encompasses (k*on, _k_off) for GFP-GR. In an attempt to achieve this, we reduced our bleach spot size to 0.5 _μ_m and then remeasured FRAP recoveries. Both the effective diffusion and full model now yielded reasonably good fits to these data (Fig. 5 F), but the full model fit yielded a clear improvement in the sum of residuals (Table 1). This is in contrast to the larger spot size examined first (1.1 _μ_m), where the sum of residuals did not change appreciably between the effective diffusion and full model fits (Table 1). For the smaller spot size, the difference in the sum of residuals between the full model and effective diffusion fits equaled 0.5 (summed over 64 data points). This placed the recovery in the boundary zone between these two regimes, which we earlier defined operationally as a sum of residuals equal to 1 (but summed over 200 data points, see Fig. 3 C). Very little additional improvement in the sum of residuals was seen with a two-state full model compared to a one-state full model (Table 1), suggesting that normally GFP-GR in the nucleus occupies predominantly one binding state. The one-binding state full model fit for the smaller spot size also yielded independent estimates for k*on and _k_off. Their ratio (5.1 ± 1.1) was in good agreement with that obtained directly via the effective diffusion fit (using Eqs. 9 and 10) for the larger spot size (6.0 ± 0.34). This agreement for different spot sizes is a satisfying confirmation of the experimental and modeling protocols.
TABLE 1.
Summary of model fits to large and small bleach spot FRAPs in control cells
| Large spot size (w = 1.1 _μ_m) | Small spot size (w = 0.5 _μ_m) | |
|---|---|---|
| Model fit | Σ Residuals | Σ Residuals |
| RD | 1.78 | 3.80 |
| ED | 0.75 | 2.41 |
| FM | 0.73 | 1.91 |
| Two-state FM | 0.73 | 1.90 |
The preceding fits illustrate several key points about GFP-GR binding within nuclei. First, they suggest that there is predominantly one binding state for GFP-GR, since the one-binding-state full model yielded a satisfactory fit that was little improved by adding a second state. Second, by using the fitted pseudo-equilibrium binding constant 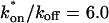 for this predominant binding state, we can calculate, using Eq. 5, that 14% of GFP-GR is free whereas 86% is bound. Before this analysis, it was not appreciated that such a large fraction of GFP-GR is bound in the nucleus. Since GFP-GR is probably overexpressed approximately five times relative to endogenous GR levels (unpublished observations), this suggests that there must be many binding sites of this predominant state within the nucleus. Third, the transient nature of this binding was also not appreciated. The effective diffusion fit for the larger spot size indicates that on average a GFP-GR molecule undergoes multiple binding interactions within the 1.1-_μ_m-radius bleach spot during the FRAP recovery. The average binding time per site is given by
for this predominant binding state, we can calculate, using Eq. 5, that 14% of GFP-GR is free whereas 86% is bound. Before this analysis, it was not appreciated that such a large fraction of GFP-GR is bound in the nucleus. Since GFP-GR is probably overexpressed approximately five times relative to endogenous GR levels (unpublished observations), this suggests that there must be many binding sites of this predominant state within the nucleus. Third, the transient nature of this binding was also not appreciated. The effective diffusion fit for the larger spot size indicates that on average a GFP-GR molecule undergoes multiple binding interactions within the 1.1-_μ_m-radius bleach spot during the FRAP recovery. The average binding time per site is given by 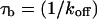 or 12.7 ms and the average time for diffusion to the next site is given by
or 12.7 ms and the average time for diffusion to the next site is given by 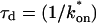 or 2.5 ms (Berg, 1986). These parameters underscore the rapid mobility of GFP-GR, indicating that on average each GFP-GR molecule samples ∼65 binding sites in 1 s. This rapid sampling of sites is likely to be important in the ability of GFP-GR to find and bind its specific DNA target site for transcription initiation.
or 2.5 ms (Berg, 1986). These parameters underscore the rapid mobility of GFP-GR, indicating that on average each GFP-GR molecule samples ∼65 binding sites in 1 s. This rapid sampling of sites is likely to be important in the ability of GFP-GR to find and bind its specific DNA target site for transcription initiation.
Based on previous studies, this bound state of GFP-GR should reflect association with the nuclear matrix (Tang and DeFranco, 1996). Since release of GR from the matrix is thought to require ATP (Tang and DeFranco, 1996), a depletion in ATP levels should lead to a smaller _k_off value as measured from a fit to the FRAP recovery.
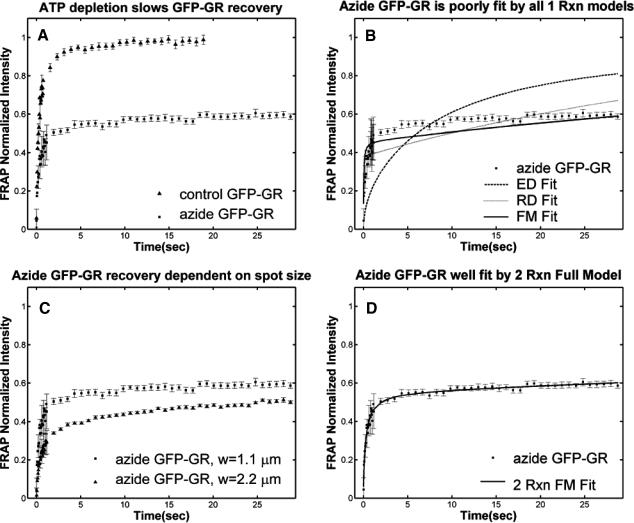
To analyze this hypothesis we performed FRAPs on cells depleted of ATP via sodium azide treatment (Tang and DeFranco, 1996). Consistent with previous observations of reduced mobility of a steroid receptor after ATP depletion (Stenoien et al., 2001), we observed a sharp decrease in the rate of FRAP recovery (Fig. 6 A). However, in contrast to the simple prediction that ATP depletion decreases _k_off, we observed that the FRAP recovery could no longer be described by any of the one-binding-state models (Fig. 6 B). This result also eliminated all multiple-state effective diffusion models, since the effective diffusion fit is unchanged by the number of binding states (see Eqs. 9 and 59).
FIGURE 6.
Sodium azide GFP-GR results. (A) Treatment with sodium azide (▪) dramatically slows the FRAP recovery of GFP-GR (w = 1.1 _μ_m, n = 10). (B) None of the single-reaction models provide a good fit to GFP-GR recovery after azide treatment. This indicates that more than one type of binding state is necessary to account for the FRAP results after azide treatment. (C) FRAPs of GFP-GR after azide treatment with different bleach spot sizes reveal a dependence on spot size and, therefore, diffusion (n = 10 in each case). (D) The reduced two-state full model (Eq. 65) consisting of an effective diffusion state plus a reaction dominant state yields a good fit (solid line) to the data (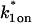 /_k_1off = 6.0,
/_k_1off = 6.0, 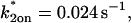 and _k_2off = 0.0043 s−1). The parameter estimates are consistent with an effective diffusion plus reaction dominant scenario. The fit was also confirmed by a fit of the full two-state model, which yields the same parameter estimates.
and _k_2off = 0.0043 s−1). The parameter estimates are consistent with an effective diffusion plus reaction dominant scenario. The fit was also confirmed by a fit of the full two-state model, which yields the same parameter estimates.
Therefore we explored reaction dominant or full models with two binding states to account for the GFP-GR recovery after azide treatment. To distinguish between these, we assessed diffusion's role by bleaching with different spot sizes (Fig. 6 C). We again found differences in recovery, suggesting that a reaction dominant model was once more inappropriate. Indeed, although such a two-state reaction dominant model yielded a good fit (data not shown), the predicted rate constants for the first of the two reactions was not in the reaction dominant regime, but rather in the full model regime 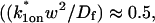 see Fig. 3 D). This inappropriate location of rate constants invalidates the fit. This fact and the dependence on bleach spot size ruled out a two-binding-state reaction dominant model.
see Fig. 3 D). This inappropriate location of rate constants invalidates the fit. This fact and the dependence on bleach spot size ruled out a two-binding-state reaction dominant model.
Together these results pointed to a two-state full model for the FRAP recovery after ATP depletion. We found indeed that such a model fit the data very well (Fig. 6 D), as judged by two different but complementary approaches. We first tested a simplified form of this two-state full model in which the first reaction lies in the effective diffusion regime and the second reaction exhibits reaction dominant behavior relative to the effective diffusion constant of the first reaction (see Appendix section Reduction of Full Two-Binding-State Model to Reduced Two-State Model). Such FRAP recoveries can be separated into two largely independent phases. The first, relatively faster phase arises due to effective diffusion of the first binding state, whereas the second, much slower phase arises due to reaction dominant behavior of the second binding state. The FRAP recovery mimics a one-state reaction dominant recovery, except that the diffusive phase is no longer instantaneous because it is governed by a slowed effective diffusion constant established by the first binding state. We refer to this simplified two-state model as the reduced two-state model because it depends on only three parameters instead of four (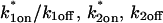 ).
).
This reduced two-state model yielded good fits to the experimental data (Fig. 6 D). We also tried the two-state full model, and obtained equally good fits (data not shown). Either approach yielded very similar predicted parameters, 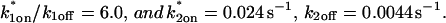 These parameters are self-consistent:
These parameters are self-consistent:
- The two-state full model predicts parameters
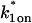 and _k_1off that are in the effective-diffusion regime
and _k_1off that are in the effective-diffusion regime 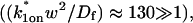 and whose ratio agrees with the ratio directly predicted by the simplified two-state model
and whose ratio agrees with the ratio directly predicted by the simplified two-state model 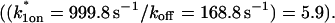
- The rate constants of the second reaction are in the reaction-dominant regime determined by _D_1eff of the first reaction (
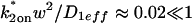 ), which is the primary requirement for the reduced two-state model.
), which is the primary requirement for the reduced two-state model.
Given the good fit, its self-consistency, and the dependence on bleach spot size, we conclude that the GFP-GR recovery after ATP depletion is governed by this reduced two-state model. The significance of this fit is that it suggests that after ATP depletion there are two binding states for GFP-GR. Using the expressions in Eq. 54 (see Appendix), we can calculate the fraction of GFP-GR in each of these two binding states. We find that 48% is bound in the first state exhibiting effective diffusion behavior, and 44% is bound in the second state exhibiting reaction dominant behavior. Thus sizable fractions of GFP-GR are present in both of these states, compared to normal cells where the FRAP recovery predicted only a single, predominant binding state. This suggests therefore that at least one new binding state and possibly two new states (if the original state is lost) arise after ATP depletion.
In fact, our data suggest that the original binding state is not lost after ATP depletion. The first binding state detected in FRAP recoveries after ATP depletion exhibited effective diffusion behavior with a pseudo-equilibrium binding constant of 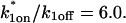 This is identical to the original
This is identical to the original 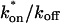 characterizing the effective diffusion behavior of the predominant binding state in control cells (Table 2). However, in control cells, 86% of GFP-GR molecules are bound at sites exhibiting this pseudo-equilibrium constant whereas, after ATP depletion, only 48% of molecules are still bound in this state. This drop after ATP depletion is a result of the 44% of GFP-GR molecules now in a second, tightly bound state. The simplest interpretation therefore is that ATP depletion induces a second state and leaves the first state relatively unchanged (Table 2).
characterizing the effective diffusion behavior of the predominant binding state in control cells (Table 2). However, in control cells, 86% of GFP-GR molecules are bound at sites exhibiting this pseudo-equilibrium constant whereas, after ATP depletion, only 48% of molecules are still bound in this state. This drop after ATP depletion is a result of the 44% of GFP-GR molecules now in a second, tightly bound state. The simplest interpretation therefore is that ATP depletion induces a second state and leaves the first state relatively unchanged (Table 2).
TABLE 2.
Pseudo-equilibrium binding constant estimated by different experiments
| FRAP experiment | 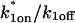 |
|---|---|
| Control, large bleach spot (ED fit) | 6.0 ± 0.34 |
| Control, small bleach spot (FM fit) | 5.1 ± 1.10 |
| Azide (first reaction of two-state FM fit) | 6.0 ± 0.77 |
This second state has the properties of the nuclear matrix. Its predicted off-rate (_k_2off = 0.0044 s−1) after ATP depletion is quite slow, consistent with biochemical analyses showing that after ATP depletion, GR is tightly bound to the nuclear matrix (Tang and DeFranco, 1996). If this second state is the nuclear matrix, then the FRAP fit predicts that 44% of GFP-GR molecules should be associated with it after ATP depletion. To test this prediction, we subjected cells to ATP depletion followed by nuclear matrix extraction, and then measured the amount of GFP-GR fluorescence retained in nuclei (Fig. 7). Remarkably, this value was 40 ± 8%, in good agreement with the value predicted independently from the FRAP fit (44%). In contrast, only 5 ± 1% of GFP-GR was associated with the matrix fraction in control cells. With our current FRAP procedure, our FRAP fits did not detect this second fraction in control cells, perhaps because it is too small to be detected above the noise. Alternatively, as some have argued, the process of nuclear-matrix extraction could induce such an association artifactually (Pederson, 2000). Our data at this time cannot distinguish between these possibilities. Nevertheless, it is clear that, at best, only a small fraction of GFP-GR is associated with the nuclear matrix in control cells, and that another predominant state exists and remains to be identified. Overall, our experimental measurements of GFP-GR association with the nuclear matrix and the predicted fractions obtained from FRAP curves are quite consistent. These results support both our modeling approach and the contention that this second state is the nuclear matrix.
Our analysis therefore suggests that normally, most of the GR does not associate with the nuclear matrix, but rather with another, as-yet unidentified binding state. However, upon ATP depletion, a significant fraction of GR molecules becomes matrix-associated. The identity of the predominant binding state in normal cells is at present unknown, but an attractive possibility is DNA. As Schaaf and Cidlowski (2003) have argued, there are presumably not enough specific DNA sites in the genome to bind the large amounts of GFP-GR expressed in a typical cell line. Indeed our analysis shows that ∼86% of GFP-GR molecules in the cell associate with sites from this first binding state. One intriguing hypothesis is that this state reflects GFP-GR binding to nonspecific DNA sites. In addition to binding tightly to their promoter sequences, all transcription factors also exhibit nonspecific DNA binding to all other sequences. Such nonspecific binding is therefore unavoidable in a genome containing 109 basepairs. If what we measure by FRAP is GFP-GR bound to nonspecific DNA sites, then our data would indicate first that one GFP-GR molecule samples ∼65 nonspecific sites per second, and second that the process measured by the FRAP recovery is in fact the search for a specific site among nonspecific ones. This is an interesting possibility worthy of further study.
Regardless of the nature of this binding state, our application of FRAP models to experimental data has highlighted several advantages of our approach. One is that our method allows for three self-consistency checks. The first is to determine if the recovery depends on bleach spot size. If a good fit is obtained using a reaction dominant model, but the recovery depends on bleach spot size, then the fit is suspect. Also suspect is a good fit obtained with an effective diffusion or full model, but with no dependence on bleach spot size. A second self-consistency check is to determine if the rate constants predicted from the fit actually lie in the correct regime of parameter space. If they do not, then once again a good fit becomes suspect. The third self-consistency check combines the first two: sufficient changes in bleach spot size will sometimes shift the FRAP recovery into a different model regime. This can provide an independent set of FRAP data to be fit by a different form of the model. Then the predicted rate constants from each case can be compared to see if they agree.
In our view, the key advantage of our, or for that matter, any quantitative approach to FRAP is that it can provide detailed insight into the meaning of the FRAP recovery. Our analysis clarifies the roles of diffusion, binding, and the number of binding states contributing to a FRAP recovery. Without such a quantitative analysis, it is difficult to infer very much from just the shape of a FRAP curve. For example, all of the recoveries generated by our models exhibit a fast early phase followed by a slower later phase. In some cases (reaction dominant behavior), this corresponds to two binding states, one weak and the other tight. In most cases, however (i.e., effective diffusion and full model), such curves reflect one or more binding states coupled to diffusion. Equally difficult to interpret are changes in shape of a FRAP curve after experimental perturbation. For example, we found that slower FRAP recoveries after ATP depletion were not simply a consequence of tighter binding in the original state. Rather, they reflected the emergence of a second binding state, which was either absent originally or present at very low levels. Thus a failure to adequately or correctly model the FRAP recovery curve will lead to erroneous conclusions. It is our hope that the set of model equations described here and the procedure for applying them will provide a more systematic approach to FRAP analysis, and enable greater and more accurate insight into the biological processes underlying a FRAP recovery.
Acknowledgments
The experimental data were collected in the National Cancer Institute fluorescence imaging facility. We thank Dr. Tatiana Karpova for expert technical assistance.
APPENDIX
Laplace transform solution of the reaction-diffusion equations
Using the change of variables, _u = F_eq − f and _v = C_eq − c, the expressions in Eq. 3 become
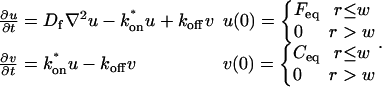 |
(12) |
|---|
Taking the Laplace transform 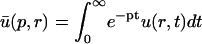 yields
yields
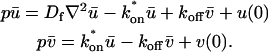 |
(13) |
|---|
The second equation can be solved for 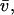 yielding
yielding
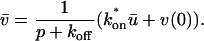 |
(14) |
|---|
Substituting this into the first equation in Eq. 13 and rearranging terms yields
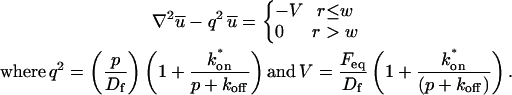 |
(15) |
|---|
This equation is of the general form given in Carslaw and Jaeger (1959) for heat conduction between composite cylinders. Using a strategy comparable to theirs, a solution is of the form
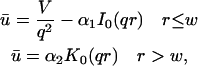 |
(16) |
|---|
where _I_0 and _K_0 are modified Bessel functions of the first and second kind. The constants _α_1 and _α_2 are determined by the requirements that 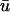 and its first derivative be continuous across the bleach spot boundary at r = w. Using the relationships between Bessel functions, _I_′0 = _I_1 and _K_′0 = −_K_1, the continuity requirement yields
and its first derivative be continuous across the bleach spot boundary at r = w. Using the relationships between Bessel functions, _I_′0 = _I_1 and _K_′0 = −_K_1, the continuity requirement yields
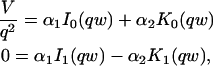
which can be solved for _α_1 and _α_2. The solution for _α_1 is
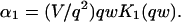 |
(17) |
|---|
Substitution for _α_1 in the first equation of the expressions in Eq. 16 provides the solution for 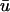 within the bleach spot.
within the bleach spot.
Since the FRAP recovery is the sum of the free (f = _F_eq − u) and bound fluorescence (c = _C_eq − v), we must compute the Laplace transform for this sum f + c = 1 − u − v. This yields the Laplace transform of the fluorescence intensity as a function of radial position within the bleach spot as
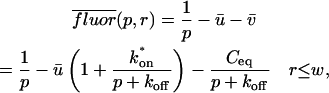 |
(18) |
|---|
where Eq. 14 was substituted for  with v(0) = _C_eq (see Eq. 12).
with v(0) = _C_eq (see Eq. 12).
To obtain the measured FRAP recovery, we must compute the average fluorescent intensity within the bleach spot. The only term in Eq. 18 that depends on r is  so it suffices to calculate the average of
so it suffices to calculate the average of  within the bleach spot and then substitute into Eq. 18:
within the bleach spot and then substitute into Eq. 18:
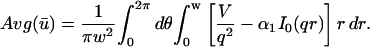 |
(19) |
|---|
Using the relationship between Bessel functions, (_rI_1(r))′ = _rI_0(r), from Eq. 19 we obtain
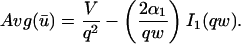 |
(20) |
|---|
Taking the average of Eq. 18 and substituting Eq. 20 for Avg(ū) yields the Laplace transform of the FRAP recovery,
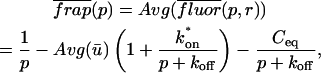 |
(21) |
|---|
which reduces to
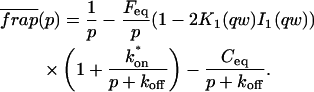 |
(22) |
|---|
The actual recovery is obtained by numerical inversion of this transform, using the Matlab routine invlap.m (Hollenbeck, 1998).
Derivation of reaction dominant solution
In the reaction dominant scenario, diffusion occurs so rapidly that it is not detected in the FRAP recovery. As a consequence, free molecules instantly equilibrate after the bleach and _f = F_eq, a constant. Thus, the first equation in the expressions in Eq. 3 disappears and the second equation becomes
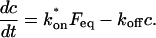 |
(23) |
|---|
Note that the first term on the right is a constant, so this is a first-order linear equation whose general solution is known and in this case given by
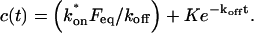 |
(24) |
|---|
By the equilibrium relationship (Eq. 4) the first term simplifies to _C_eq. The constant K is evaluated by the initial condition c(0) = 0, reflecting the fact that after normalization the concentration of fluorescent molecules in the bleach zone is zero. This leads to the solution
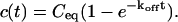 |
(25) |
|---|
The preceding equation yields the behavior for the bound complex of fluorescent protein. Total fluorescence f(t) + c(t) is
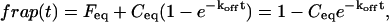 |
(26) |
|---|
where we have used the fact that _F_eq + _C_eq = 1.
Note that the preceding equations (unlike those for the full model, pure-diffusion dominant or effective diffusion) do not depend on the shape of the bleached region.
Derivation of idealized solutions from the full model
We show here how the full model solution (Eq. 22) reduces to each of the idealized scenarios when a particular constraint defined in Fig. 3 C is applied. For each idealized domain, the general approach is to define dimensionless variables, scaling space by the bleach spot size w, and scaling time by the characteristic timescale τ for that idealized domain as
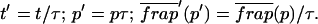 |
(27) |
|---|
Reduction of full model to pure-diffusion dominant
For pure-diffusion dominant, the timescale is 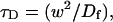 and from Fig. 3 C the constraint is
and from Fig. 3 C the constraint is 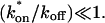 With this constraint applied to Eq. 5, _F_eq ≈ 1, _C_eq ≈ 0. Also,
With this constraint applied to Eq. 5, _F_eq ≈ 1, _C_eq ≈ 0. Also, 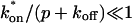 and therefore from Eq. 15
and therefore from Eq. 15 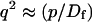 and so
and so 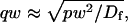 which by Eq. 27 is
which by Eq. 27 is 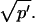 By defining
By defining 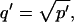 Eq. 22 reduces to
Eq. 22 reduces to
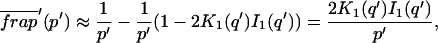 |
(28) |
|---|
in which we recognize Eq. 28 as the product of two entities that have known inverse Laplace transforms (Crank, 1975),
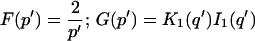 |
(29) |
|---|
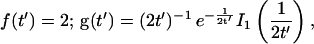 |
(30) |
|---|
where f and g are the inverse Laplace transforms of F and G, respectively. Using the convolution property of the Laplace transform, 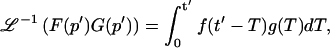 the inverse Laplace transform of Eq. 28 is
the inverse Laplace transform of Eq. 28 is
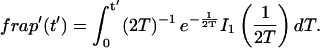 |
(31) |
|---|
Changing variables via 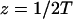 yields
yields
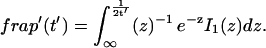 |
(32) |
|---|
Evaluating this integral and determining the behavior at z = ∞ using Eq. 9.7.1 in Abramowitz and Stegun (1972), we find
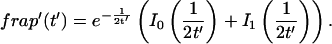 |
(33) |
|---|
One can check this integral evaluation directly by differentiation, using 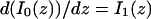 and
and 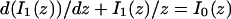 (Watson, 1944). Using the relationships in the expressions in Eq. 27 with
(Watson, 1944). Using the relationships in the expressions in Eq. 27 with 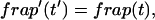 we can then obtain
we can then obtain
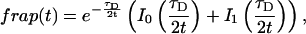 |
(34) |
|---|
which is precisely Eq. 8, the solution obtained by Soumpasis for a freely diffusing molecule bleached with a circular spot.
Reduction of full model to effective diffusion
The constraint for effective diffusion from Fig. 3 C is 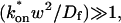 and the appropriate timescale is
and the appropriate timescale is 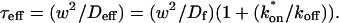 Simplification of Eq. 22 begins by noting that
Simplification of Eq. 22 begins by noting that
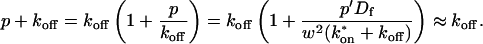 |
(35) |
|---|
After dividing through by _τ_eff, the full model solution (Eq. 22) becomes
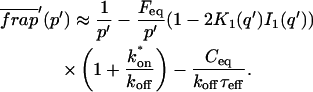 |
(36) |
|---|
The last term is negligible because the denominator 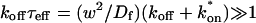 by the effective diffusion constraint. Finally, since by Eq. 5,
by the effective diffusion constraint. Finally, since by Eq. 5, 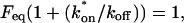 Eq. 36 reduces to
Eq. 36 reduces to
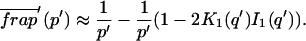 |
(37) |
|---|
This is identical to Eq. 28, the pure-diffusion dominant solution, and again by inverse Laplace transformation leads to the Soumpasis equation for a circular bleach spot (Eq. 8), but now with 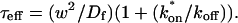
Reduction of full model to reaction dominant
The constraints for reaction dominant behavior from Fig. 3 C are 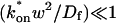 and
and 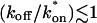 (_C_eq ≠ 0). The appropriate timescale is
(_C_eq ≠ 0). The appropriate timescale is 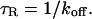 Under these conditions, the argument qw for the Bessel functions in Eq. 22 can be obtained from the relationship
Under these conditions, the argument qw for the Bessel functions in Eq. 22 can be obtained from the relationship
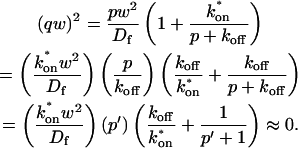 |
(38) |
|---|
For qw → 0, _K_1(qw)_I_1(qw) ≈ 0.5, and the factor (1−2_K_1(qw)_I_1(qw)) in the second term of Eq. 22 is negligible and so the full model for the reaction dominant scenario becomes 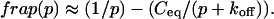 Dividing by _τ_R yields a solution on the reaction timescale of
Dividing by _τ_R yields a solution on the reaction timescale of 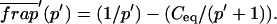 The inverse transform then yields the reaction dominant solution Eq. 11.
The inverse transform then yields the reaction dominant solution Eq. 11.
Transition between the pure-diffusion dominant regime and reaction dominant regime
To investigate the crossover between the pure-diffusion dominant and reaction dominant regimes, we evaluate the full model in the lower half of the plot in Fig. 3 C, namely with 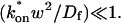 Scaling Eq. 22 to _τ_D and using the dimensionless variables of Eq. 27 yields the following equation for the full model:
Scaling Eq. 22 to _τ_D and using the dimensionless variables of Eq. 27 yields the following equation for the full model:
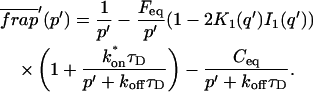 |
(39) |
|---|
Given that 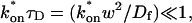 this reduces to
this reduces to
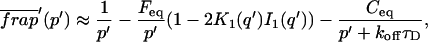 |
(40) |
|---|
which can be rewritten as
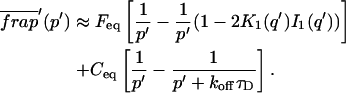 |
(41) |
|---|
where we recognize the term inside the first brackets as the pure-diffusion dominant solution, and the term inside the second brackets as a single exponential solution, corresponding to that obtained in the reaction dominant case when _C_eq = 1 (_k_off ≪ k*on). Thus for 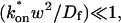 the FRAP recovery is composed of two independent terms, one for pure-diffusion and one for reaction behavior. The contribution of each term is determined by the size of _F_eq and _C_eq.
the FRAP recovery is composed of two independent terms, one for pure-diffusion and one for reaction behavior. The contribution of each term is determined by the size of _F_eq and _C_eq.
Transition between reaction dominant to effective diffusion regimes
The crossover between the reaction dominant and effective diffusion regimes occurs when 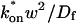 goes from small to large in the left half of the plot in Fig. 3 C. If _k_off ≪ k*on, then we avoid traversing a region where only the full model is valid. Instead, we find a crossover model somewhat simpler than the full model, which we refer to as hybrid behavior. Adding the expressions in Eq. 12 and using the second expression in Eq. 12 to substitute for u, we obtain
goes from small to large in the left half of the plot in Fig. 3 C. If _k_off ≪ k*on, then we avoid traversing a region where only the full model is valid. Instead, we find a crossover model somewhat simpler than the full model, which we refer to as hybrid behavior. Adding the expressions in Eq. 12 and using the second expression in Eq. 12 to substitute for u, we obtain
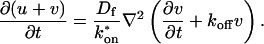 |
(42) |
|---|
With _k_off ≪ _k_on, the free fraction is negligible, and so by Eqs. 5 and 12, u + v ≈ v, giving
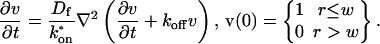 |
(43) |
|---|
This hybrid model has one less fitting parameter than the full model, since 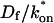 only appears as a ratio. The significance of this hybrid model is that it fits the full model well in a large portion of the full-model-only domain (see Fig. 8), and therefore in this region the full model is capable of predicting only the ratio
only appears as a ratio. The significance of this hybrid model is that it fits the full model well in a large portion of the full-model-only domain (see Fig. 8), and therefore in this region the full model is capable of predicting only the ratio 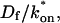 rather than unique values for each parameter. However, since in practice _D_f can be determined, both the full model and this slightly simpler hybrid model will be fit with the same number of parameters. The Laplace transform of the solution may be obtained directly as in the first section of the Appendix or from the full model by approximation as follows.
rather than unique values for each parameter. However, since in practice _D_f can be determined, both the full model and this slightly simpler hybrid model will be fit with the same number of parameters. The Laplace transform of the solution may be obtained directly as in the first section of the Appendix or from the full model by approximation as follows.
The dimensionless variables (Eq. 27) can be used, in this case with the reaction timescale 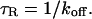 By the penultimate term in Eq. 38 with
By the penultimate term in Eq. 38 with 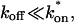 the Bessel function argument in Eq. 22 can be obtained from the relationship
the Bessel function argument in Eq. 22 can be obtained from the relationship
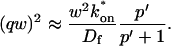 |
(44) |
|---|
Letting _q_′ = qw, the full model (Eq. 22) can be rewritten as
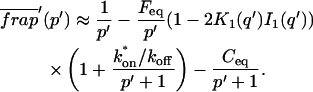 |
(45) |
|---|
Since 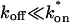 and
and 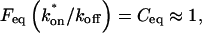 Eq. 45 reduces to
Eq. 45 reduces to
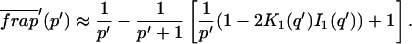 |
(46) |
|---|
Note that unlike the transition from pure-diffusion dominant to reaction dominant behavior, the solution in this hybrid diffusion regime cannot be written as the sum of two independent terms representing diffusion and reaction, but rather is a more complicated combination of these behaviors.
One can also observe how the hybrid model (Eq. 46) reduces to either the reaction dominant case or effective diffusion for small or large values of 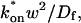 respectively. With
respectively. With 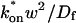 small, _q_′ ≈ 0, yielding 2_K_1(_q_′)_I_1(_q_′) ≈ 1 and Eq. 46 reduces to the reaction dominant solution with _C_eq = 1,
small, _q_′ ≈ 0, yielding 2_K_1(_q_′)_I_1(_q_′) ≈ 1 and Eq. 46 reduces to the reaction dominant solution with _C_eq = 1,
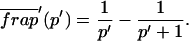 |
(47) |
|---|
To observe effective diffusion behavior, the initial time variables t and p must be scaled to the effective diffusion timescale 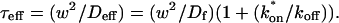 Note that in the hybrid model,
Note that in the hybrid model, 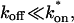 so
so 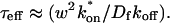 The primed variables in Eq. 46 have already been scaled by 1/_k_off, so they need only be scaled by
The primed variables in Eq. 46 have already been scaled by 1/_k_off, so they need only be scaled by 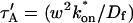 to achieve the effective diffusion timescale _t_″,
to achieve the effective diffusion timescale _t_″,
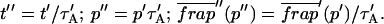 |
(48) |
|---|
With 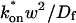 large,
large, 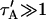 and the Bessel function argument in Eq. 22 can be obtained via Eq. 44 as
and the Bessel function argument in Eq. 22 can be obtained via Eq. 44 as
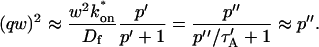 |
(49) |
|---|
Eq. 46 now becomes
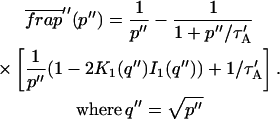 |
(50) |
|---|
Again with 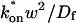 large,
large, 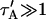 and Eq. 50 reduces to
and Eq. 50 reduces to
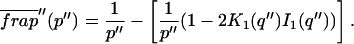 |
(51) |
|---|
This is the effective diffusion solution operating on the approximate effective diffusion timescale 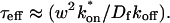
FIGURE 8.
Hybrid model results. We have found a simplified model that depends on only two parameters, _D_f / and _k_off, which provides a good fit (sum of residuals <1) to the full model when _k_off ≪
and _k_off, which provides a good fit (sum of residuals <1) to the full model when _k_off ≪  (area above solid line; _D_f = 30 _μ_m2/s, w = 0.5 _μ_m). This hybrid model describes the crossover between the reaction and effective diffusion regimes (compare to Fig. 3 C), and mathematically reduces to either the reaction dominant equation or the effective diffusion equation with
(area above solid line; _D_f = 30 _μ_m2/s, w = 0.5 _μ_m). This hybrid model describes the crossover between the reaction and effective diffusion regimes (compare to Fig. 3 C), and mathematically reduces to either the reaction dominant equation or the effective diffusion equation with  small or
small or  large, respectively. Practically, the hybrid model demonstrates that a large portion (shaded area) of the previously identified full-model-only zone (see Fig. 3 C) is dependent on only two parameters: _D_f /
large, respectively. Practically, the hybrid model demonstrates that a large portion (shaded area) of the previously identified full-model-only zone (see Fig. 3 C) is dependent on only two parameters: _D_f /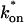 and _k_off. Therefore it is important that _D_f be determined before attempting to extract the rate constants from the full model.
and _k_off. Therefore it is important that _D_f be determined before attempting to extract the rate constants from the full model.
Two-binding-state model
When a second, independent binding state is present, the chemical rate equations become
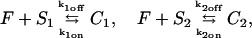 |
(52) |
|---|
where subscripts 1 and 2 refer to the different binding states. With the same assumptions that led to Eq. 3 for the one-state model, the new equations describing FRAP recovery are
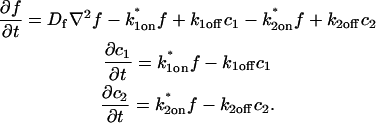 |
(53) |
|---|
Solving for equilibrium yields the following relationships:
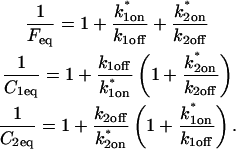 |
(54) |
|---|
Laplace transform solution of full two-binding-state model
In the full reaction diffusion model, the Laplace transform can also be applied as in the single reaction case, but two changes arise. The expression for the Laplace transform of the FRAP recovery generalizes to
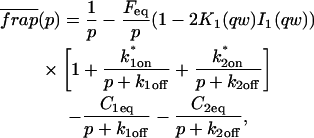 |
(55) |
|---|
with a new formula for the parameter q as
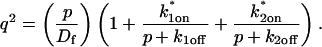 |
(56) |
|---|
Reduction of full two-binding-state model to pure-diffusion dominant
For the new system (expressions in Eq. 53), the pure-diffusion dominant scenario is once again trivial. If for both binding states, the off-rates are large relative to the pseudo-on rates, then by Eq. 54, _F_eq ≈ 1 and _C_1eq ≈ _C_2eq ≈ 0, so most of the fluorescence will be free and therefore still satisfy the FRAP for free diffusion (Eq. 8).
Reduction of full two-binding-state model to effective diffusion
Under conditions where binding in both states is rapid compared to the diffusion timescale, the effective diffusion scenario holds. Following Crank's derivation (Crank, 1975), the expressions in Eq. 53 can be rewritten for two independent binding reactions as
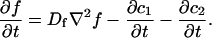 |
(57) |
|---|
In the effective diffusion regime, diffusion drives changes in concentration within the bleach spot, but at any moment or location, the two binding states rapidly achieve local equilibrium. At all local equilibria, the last two relations in the expressions in Eq. 53 imply that 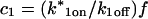 and
and 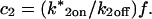 Substitution into the first equation of the expressions in Eq. 53 yields
Substitution into the first equation of the expressions in Eq. 53 yields
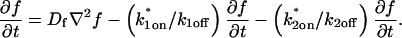 |
(58) |
|---|
Collecting terms for 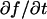 yields the standard diffusion equation, but with
yields the standard diffusion equation, but with
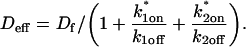 |
(59) |
|---|
Thus, when effective diffusion holds, the resultant FRAP curve will be fit by the diffusion model (Eq. 8), and the fit will yield an estimate for _D_eff. This value will only determine the sum of the two pseudo-equilibrium constants in Eq. 59, so extracting additional information about specific off- and pseudo-on rates for each of the binding states will be impossible with FRAP. Indeed, without experiments to specifically disrupt one state, it will be impossible to distinguish between a one-state or a multistate model when effective diffusion holds.
Reduction of full two-binding-state model to reaction dominant
In a reaction dominant scenario with two binding states, each state yields an equation like Eq. 23 (see Derivation of Reaction Dominant Solution in Appendix) that can be solved independently to yield a result like Eq. 11. The total fluorescence intensity is then the sum of _F_eq + _c_1(t) + _c_2(t),
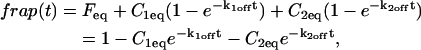 |
(60) |
|---|
where the equilibrium concentrations are determined by the expressions in Eq. 54, and _F_eq + _C_1eq + _C_2eq = 1. Thus in a well-mixed case of two binding states, the FRAP recovery should be a sum of two exponentials requiring a four-parameter fit. The fit yields two off-rates from the combined FRAP recovery rate, and also yields the pseudo-on rates indirectly by substitution for _C_1eq and _C_2eq from the expressions in Eq. 54.
Reduction of full two-binding-state model to reduced two-state model
In this scenario, the first reaction lies in the effective diffusion regime governed by the constraint 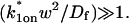 The second reaction lies in a reaction dominant regime defined by the effective diffusion constant _D_1eff of the first binding reaction and governed by the constraint
The second reaction lies in a reaction dominant regime defined by the effective diffusion constant _D_1eff of the first binding reaction and governed by the constraint 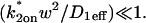 The resultant FRAP resembles a reaction dominant recovery for a single binding state, but with the diffusive phase of the recovery determined exclusively by _D_1eff of the first binding state and the exponential recovery rate of the reaction phase determined exclusively by _k_2off of the second binding state.
The resultant FRAP resembles a reaction dominant recovery for a single binding state, but with the diffusive phase of the recovery determined exclusively by _D_1eff of the first binding state and the exponential recovery rate of the reaction phase determined exclusively by _k_2off of the second binding state.
The reduction of the two-state model proceeds by analyzing its behavior on the effective diffusion timescale of the first reaction as
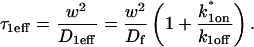 |
(61) |
|---|
On this timescale, the effective diffusion constraint yields two simplifications in Eq. 55 for the two-state model. First, by analogy with the argument in Eq. 35, p + _k_1off ≈ _k_1off . With this and after dividing Eq. 55 by _τ_1eff, the two-state model can be rewritten as
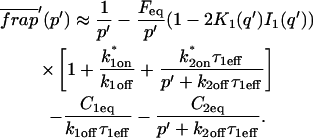 |
(62) |
|---|
Second, by the argument leading to Eq. 37, _k_1off_τ_1eff ≫ 1, so 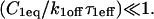 The reaction dominant constraint
The reaction dominant constraint 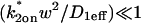 is simply k*2on_τ_1eff ≪ 1, so the term
is simply k*2on_τ_1eff ≪ 1, so the term 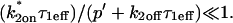 Thus Eq. 62 reduces to
Thus Eq. 62 reduces to
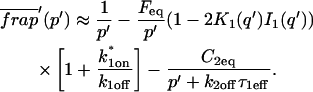 |
(63) |
|---|
It can be shown that 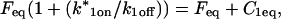 allowing Eq. 63 to be rewritten as
allowing Eq. 63 to be rewritten as
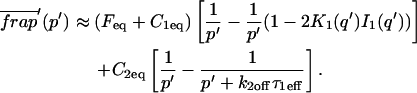 |
(64) |
|---|
Multiplying through by _τ_1eff and then computing the inverse Laplace transform yields
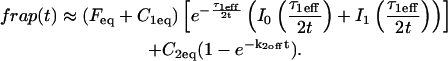 |
(65) |
|---|
The first term is a diffusion solution weighted by the fraction of molecules exhibiting effective diffusion. The second term is a reaction dominant solution weighted by the fraction of bound molecules in this second binding state. FRAP data may be fitted directly with this solution which involves three parameters, 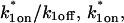 and _k_2off. Alternatively, the full model with one binding state may be used to estimate three pseudo-one-binding state parameters: D,
and _k_2off. Alternatively, the full model with one binding state may be used to estimate three pseudo-one-binding state parameters: D, 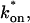 and _k_off. By noting the similarities between Eqs. 64 and 41, and noting that the predicted D corresponds to _D_1eff, the actual two-binding-state parameters can be obtained from the following relationships: _k_2off = _k_off,
and _k_off. By noting the similarities between Eqs. 64 and 41, and noting that the predicted D corresponds to _D_1eff, the actual two-binding-state parameters can be obtained from the following relationships: _k_2off = _k_off, 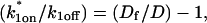 and
and 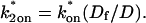
Analysis of rate-constant parameter space for the two-binding-state model
Using the preceding equations, it is possible to investigate the behavior of the two-binding-state full model, and determine when the idealized cases hold. However, an exhaustive evaluation of this model is complicated because the rate-constant parameter space is four-dimensional and therefore, difficult to visualize. In addition, the time required to cycle through all permutations of the four rate constants becomes prohibitive. Nevertheless we have explored this parameter space sufficiently to arrive at several conclusions. First, as with the one-binding-state scenario, the observed FRAP behaviors can be divided into the same four categories: pure-diffusion dominant, effective diffusion, reaction dominant, and full model. As with the one-binding-state model, the full model for two binding states is sometimes very well approximated by one of the three idealized cases for two binding states, but for some combinations of rate constants, the full model result is unique (Fig. 4).
To determine what values of rate constants yield specific behaviors, we used as a guide the rate-constant parameter space map for the one-binding-state model. By testing thousands of combinations of rate-constant values, we identified several rules based on combinations of reactions from the same or different domains of parameter space defined for the one-binding-state model. Reactions that lie in the same domain of the one-binding-state model when combined still yield a reaction in that domain (Fig. 4, first column: A, D, and G). For example, if each reaction alone is in the effective diffusion domain of the one-state model, then the combined reaction will also be in that domain in the two-state model (Fig. 4 A). However, when reactions from different regimes of the one-state model are combined, then the result is typically in the full model regime for the two-state model (Fig. 4, second column: B, E, and H). For example, combining a reaction dominant state with any other state yields full model behavior (Fig. 4, E and H). Thus the full model regime occupies a larger domain in the rate-constant parameter space as the number of reactions is increased.
Exceptions to the preceding rule arise when one of the reactions dominates either due to its relative concentration or time for recovery (Fig. 4, third column: C and F). For example, if the equilibrium concentration of binding state 2 is much higher than binding state 1, then most of the FRAP recovery will be dominated by state 2 and so exhibit the behavior characteristic of the rate constants for state 2 (Fig. 4 C). Similarly, if the time for recovery of state 2 is much longer than state 1, then the FRAP recovery will be reasonably well fit by the idealized model for state 2 (Fig. 4 F). In essence these limiting cases are not of great biological interest, because the contribution of one state to the FRAP recovery is small, and so will go largely unnoticed experimentally. What is of biological significance is the fact that the same idealized behaviors occur for more than just one binding state, and that the idealized cases occur less frequently as the number of binding states is increased and are instead replaced with full model behavior.
Brian L. Sprague and Robert L. Pego contributed equally to this work.
References
- Abramowitz, M., and I. A. Stegun. 1972. Bessel functions of integer order. In Handbook of Mathematical Functions. Dover Publications, New York. 377.
- Arrio-Dupont, M., G. Foucault, M. Vacher, P. F. Devaux, and S. Cribier. 2000. Translational diffusion of globular proteins in the cytoplasm of cultured muscle cells. Biophys. J. 78:901–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg, O. G. 1986. Effective diffusion rate through a polymer network: influence of nonspecific binding and intersegment transfer. Biopolymers. 25:811–821. [DOI] [PubMed] [Google Scholar]
- Berk, D. A., F. Yuan, M. Leunig, and R. K. Jain. 1997. Direct in vivo measurement of targeted binding in a human tumor xenograft. Proc. Natl. Acad. Sci. USA. 94:1785–1790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulinski, J. C., D. J. Odde, B. J. Howell, E. D. Salmon, and C. M. Waterman-Storer. 2001. Rapid dynamics of the microtubule binding of ensconsin in vivo. J. Cell Sci. 114:3885–3897. [DOI] [PubMed] [Google Scholar]
- Carrero, G., D. McDonald, E. Crawford, G. de Vries, and M. J. Hendzel. 2003. Using FRAP and mathematical modeling to determine the in vivo kinetics of nuclear proteins. Methods. 29:14–28. [DOI] [PubMed] [Google Scholar]
- Carslaw, H. S., and J. C. Jaeger. 1959. The Laplace transformation: problems on the cylinder and sphere. Composite cylindrical regions. In Conduction of Heat in Solids. Oxford University Press, New York. 345–347.
- Coscoy, S., F. Waharte, A. Gautreau, M. Martin, D. Louvard, P. Mangeat, M. Arpin, and F. Amblard. 2002. Molecular analysis of microscopic ezrin dynamics by two-photon FRAP. Proc. Natl. Acad. Sci. USA. 99:12813–12818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crank, J. 1975. Diffusion and chemical reaction. In The Mathematics of Diffusion. Oxford University Press, New York. 326–351.
- Deroo, B. J., C. Rentsch, S. Sampath, J. Young, D. B. DeFranco, and T. K. Archer. 2002. Proteasomal inhibition enhances glucocorticoid receptor transactivation and alters its subnuclear trafficking. Mol. Cell. Biol. 22:4113–4123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dou, Y., J. Bowen, Y. Liu, and M. A. Gorovsky. 2002. Phosphorylation and an ATP-dependent process increase the dynamic exchange of H1 in chromatin. J. Cell Biol. 158:1161–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dundr, M., U. Hoffmann-Rohrer, Q. Hu, I. Grummt, L. I. Rothblum, R. D. Phair, and T. Misteli. 2002. A kinetic framework for a mammalian RNA polymerase in vivo. Science. 298:1623–1626. [DOI] [PubMed] [Google Scholar]
- Edidin, M., Y. Zagyansky, and T. J. Lardner. 1976. Measurement of membrane protein lateral diffusion in single cells. Science. 191:466–468. [DOI] [PubMed] [Google Scholar]
- Elson, E. L. 1985. Fluorescence correlation spectroscopy and photobleaching recovery. Annu. Rev. Phys. Chem. 36:379–406. [Google Scholar]
- Elson, E. L. 2001. Fluorescence correlation spectroscopy measures molecular transport in cells. Traffic. 2:789–796. [DOI] [PubMed] [Google Scholar]
- Elson, E. L., and D. Magde. 1974. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 13:1–27. [DOI] [PubMed] [Google Scholar]
- Elson, E. L., and J. A. Reidler. 1979. Analysis of cell surface interactions by measurements of lateral mobility. J. Supramol. Struct. 12:481–489. [DOI] [PubMed] [Google Scholar]
- Feder, T. J., I. Brust-Mascher, J. P. Slattery, B. Baird, and W. W. Webb. 1996. Constrained diffusion or immobile fraction on cell surfaces: a new interpretation. Biophys. J. 70:2767–2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fey, E. G., G. Krochmalnic, and S. Penman. 1986. The nonchromatin substructures of the nucleus: the ribonucleoprotein (RNP)-containing and RNP-depleted matrices analyzed by sequential fractionation and resinless section electron microscopy. J. Cell Biol. 102:1654–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollenbeck, K. J. 1998. INVLAP.M: A MATLAB function for numerical inversion of Laplace transforms by the de Hoog algorithm. http://www.isva.dtu.dk/staff/karl/invlap.htm.
- Houtsmuller, A. B., and W. Vermeulen. 2001. Macromolecular dynamics in living cell nuclei revealed by fluorescence redistribution after photobleaching. Histochem. Cell Biol. 115:13–21. [DOI] [PubMed] [Google Scholar]
- Icenogle, R. D., and E. Elson. 1983. Fluorescence correlation spectroscopy and photobleaching recovery of multiple binding reactions. II. FPR and FCS measurements at low and high DNA concentrations. Biopolymers. 22:1949–1966. [DOI] [PubMed] [Google Scholar]
- Kaufman, E. N., and R. K. Jain. 1990. Quantification of transport and binding parameters using fluorescence recovery after photobleaching. Potential for in vivo applications. Biophys. J. 58:873–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman, E. N., and R. K. Jain. 1991. Measurement of mass transport and reaction parameters in bulk solution using photobleaching. Reaction limited binding regime. Biophys. J. 60:596–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, H., K. Sugaya, and P. R. Cook. 2002. The transcription cycle of RNA polymerase II in living cells. J. Cell Biol. 159:777–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman, B. A., and S. K. Nordeen. 1997. DNA intersegment transfer, how steroid receptors search for a target site. J. Biol. Chem. 272:1061–1068. [DOI] [PubMed] [Google Scholar]
- Liebman, P. A., and G. Entine. 1974. Lateral diffusion of visual pigment in photoreceptor disk membranes. Science. 185:457–459. [DOI] [PubMed] [Google Scholar]
- McNally, J. G., W. G. Muller, D. Walker, R. Wolford, and G. L. Hager. 2000. The glucocorticoid receptor: rapid exchange with regulatory sites in living cells. Science. 287:1262–1265. [DOI] [PubMed] [Google Scholar]
- Meyvis, T. K., S. C. De Smedt, P. Van Oostveldt, and J. Demeester. 1999. Fluorescence recovery after photobleaching: a versatile tool for mobility and interaction measurements in pharmaceutical research. Pharm. Res. 16:1153–1162. [DOI] [PubMed] [Google Scholar]
- Misteli, T. 2001. Protein dynamics: implications for nuclear architecture and gene expression. Science. 291:843–847. [DOI] [PubMed] [Google Scholar]
- Müller, W. G., D. Walker, G. L. Hager, and J. G. McNally. 2001. Large-scale chromatin decondensation and recondensation regulated by transcription from a natural promoter. J. Cell Biol. 154:33–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pederson, T. 2000. Half a century of “the nuclear matrix.” Mol. Biol. Cell. 11:799–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phair, R. D., and T. Misteli. 2000. High mobility of proteins in the mammalian cell nucleus. Nature. 404:604–609. [DOI] [PubMed] [Google Scholar]
- Poo, M., and R. A. Cone. 1974. Lateral diffusion of rhodopsin in the photoreceptor membrane. Nature. 247:438–441. [DOI] [PubMed] [Google Scholar]
- Reits, E. A., and J. J. Neefjes. 2001. From fixed to FRAP: measuring protein mobility and activity in living cells. Nat. Cell Biol. 3:E145–E147. [DOI] [PubMed] [Google Scholar]
- Safranyos, R. G., S. Caveney, J. G. Miller, and N. O. Peterson. 1987. Relative roles of gap junction channels and cytoplasm in cell-to-cell diffusion of fluorescent tracers. Proc. Natl. Acad. Sci. USA. 84:2272–2276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaaf, M. J. M., and J. A. Cidlowski. 2003. Molecular determinants of glucocorticoid receptor mobility in living cells: the importance of ligand affinity. Mol. Cell. Biol. 23:1922–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlessinger, J., D. E. Koppel, D. Axelrod, K. Jacobson, W. W. Webb, and E. L. Elson. 1976. Lateral transport on cell membranes: mobility of concanavalin A receptors on myoblasts. Proc. Natl. Acad. Sci. USA. 73:2409–2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siggia, E. D., J. Lippincott-Schwartz, and S. Bekiranov. 2000. Diffusion in inhomogeneous media: theory and simulations applied to whole cell photobleach recovery. Biophys. J. 79:1761–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soumpasis, D. M. 1983. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 41:95–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stenoien, D. L., K. Patel, M. G. Mancini, M. Dutertre, C. L. Smith, B. W. O'Malley, and M. A. Mancini. 2001. FRAP reveals that mobility of oestrogen receptor-alpha is ligand- and proteasome-dependent. Nat. Cell Biol. 3:15–23. [DOI] [PubMed] [Google Scholar]
- Swaminathan, R., C. P. Hoang, and A. S. Verkman. 1997. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 72:1900–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, Y., and D. B. DeFranco. 1996. ATP-dependent release of glucocorticoid receptors from the nuclear matrix. Mol. Cell. Biol. 16:1989–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tardy, Y., J. L. McGrath, J. H. Hartwig, and C. F. Dewey. 1995. Interpreting photoactivated fluorescence microscopy measurements of steady-state actin dynamics. Biophys. J. 69:1674–1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, N. L., T. P. Burghardt, and D. Axelrod. 1981. Measuring surface dynamics of biomolecules by total internal reflection fluorescence with photobleaching recovery or correlation spectroscopy. Biophys. J. 33:435–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, D., H. Htun, and G. L. Hager. 1999. Using inducible vectors to study intracellular trafficking of GFP-tagged steroid/nuclear receptors in living cells. Methods. 19:386–393. [DOI] [PubMed] [Google Scholar]
- Watson, G. N. 1944. A Treatise on the Theory of Bessel Functions. The MacMillan Company, New York.
- White, J., and E. Stelzer. 1999. Photobleaching GFP reveals protein dynamics inside live cells. Trends Cell Biol. 9:61–65. [DOI] [PubMed] [Google Scholar]