Imaging membrane potential in dendritic spines (original) (raw)

Abstract

Dendritic spines mediate most excitatory inputs in the brain. Although it is clear that spines compartmentalize calcium, it is still unknown what role, if any, they play in integrating synaptic inputs. To investigate the electrical function of spines directly, we used second harmonic generation (SHG) imaging of membrane potential in pyramidal neurons from hippocampal cultures and neocortical brain slices. With FM 4-64 as an intracellular SHG chromophore, we imaged membrane potential in the soma, dendritic branches, and spines. The SHG response to voltage was linear and seemed based on an electro-optic mechanism. The SHG sensitivity of the chromophore in spines was similar to that of the parent dendritic shaft and the soma. Backpropagation of somatic action potentials generated SHG signals at spines with similar amplitude and kinetics to somatic ones. Our optical measurements of membrane potential from spines demonstrate directly that backpropagating action potentials invade the spines.

Keywords: second-harmonic imaging, backpropagation, action potential, pyramidal, cortex

Spines mediate most excitatory contact in the mammalian nervous system, so they are likely to be crucial for brain function (1). Although their role in calcium compartmentalization has been demonstrated (2), nonspiny neurons can also compartmentalize calcium with similar spatial restriction (3), so it is likely that spines serve additional functions in dendritic integration. In particular, there is a long-standing controversy related to the electrical function of dendritic spines (4). On the one hand, it has been argued that spines could have a significant effect on the excitatory postsynaptic potentials (EPSPs) (5–7). Spines could either enhance the depolarization generated by EPSPs (8) or even filter and dampen EPSPs, as they are transmitted to the dendritic shaft or the soma. On the other hand, cable models constrained by morphological or diffusional measurements indicate that spines may not play a significant electrical role (9, 10). Thus, assuming a passive membrane, the spine neck could have a negligible effect in altering the EPSPs, so spines may play no significant electrical role and merely serve as biochemical compartments.

Recent data have reopened this debate and suggest that spines could have a significant effect on altering synaptic transmission. First, active conductances, including calcium (2), potassium (11), and probably even sodium (12) channels, seem to be located in spines, rendering passive models inadequate to explore the effect of the spine on EPSPs. Second, spines with different morphologies have differences in calcium compartmentalization (13) and in amplitude and kinetics in response to glutamate uncaging (14), raising the suspicion that the spine neck has a major functional role.

Direct measurement of electrical function of spine has eluded scientists due to lack of suitable experimental approaches. Although fluorescent voltage-sensitive dyes have been used to image dendrites (15), their lack of sensitivity, partly resulting from the lack of specificity when staining plasma vs. intracellular membranes, and poor spatial resolution make it very difficult to perform quantitative voltage measurements at spines with them. As an alternative technique, we have imaged membrane potential in spines using second harmonic generation (SHG). SHG is a nonlinear optical phenomenon that occurs specifically at interfaces with oriented arrays of chromophores (16). The exquisite sensitivity of SHG to membrane interfaces and linear dependence on electric field make it ideally suited to image membrane potential (17) or, more generally, membrane-specific cellular functions. During the last decade, the groups of Loew and Lewis (18) have designed a variety of chromophores and carried out SHG measurements of membrane potential in cultured cells. Further work from them and other groups has extended SHG measurements of voltage to invertebrate and vertebrate neurons (19–21). Our study demonstrates a further application of SHG, providing experimental measurements of voltage at spines.

Results and Discussion

Somatic SHG Responses to Slow Voltage Steps. To image membrane potential in neurons, we used FM 4-64, originally designed as a membrane recycling probe (22), as an SHG chromophore (23, 24) (Fig. 1_A_). The amphiphilic nature of FM 4-64 makes it highly water soluble, yet it has high affinity to nonpolar phospholipid bilayer and forms an ordered dense structure, whereas the charge group prevents the dye molecule from crossing the plasma membrane. These properties, together with a large charge shift, make it a good SHG probe of membrane potential.

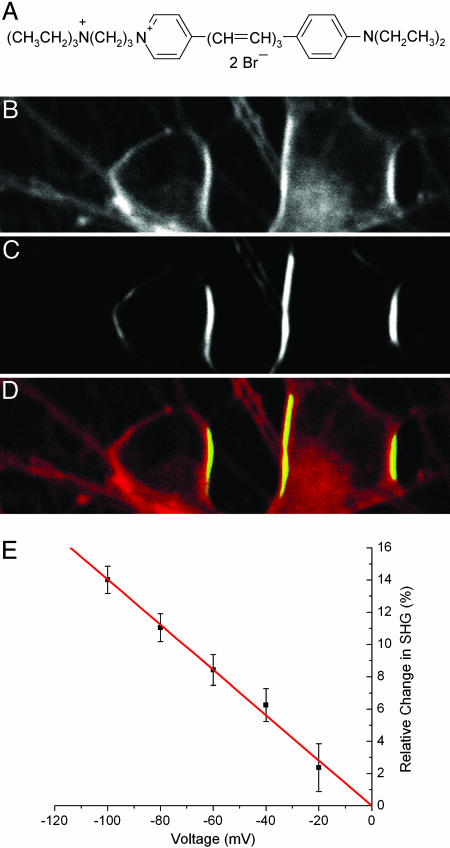
Fig. 1.

Fig. 1.

SHG imaging of cultured neurons with FM 4-64. Rat hippocampus dissociated neurons in culture 6 days in vitro externally stained with FM 4-64 (structure shown in A) and imaged with 1.5-mW average power at the sample at 900 nm, laser horizontally polarized. (B) Two-photon excitation fluorescence (TPF). (C) SHG. (D) Composite image of SHG (green) and TPF (red). (E) SHG signal versus voltage. Each data point indicates the mean of eight measurements (except at –20 mV only 4), where each error bar is the SEM. Linear regression through the origin gives a slope of –14.0 ± 0.3% per 100 mV, R = –0.996. Electrode is located at the left.

To establish the voltage sensitivity of the SHG signal, we first used FM 4-64 with extracellular bulk loading of dissociated hippocampal neuronal cultures and tested the SHG response to different voltage protocols, generated with whole-cell recording (Fig. 1). Specifically, we examined the voltage sensitivity of SHG by measuring SHG signals from the somata of whole-cell recorded neurons during different voltage-clamp protocols synchronized with frame acquisition imaging at slow (≈1 s per frame, the “framescan”) temporal resolution (see Materials and Methods). We found that SHG was remarkably linear with voltage, with a relative change of –14.0 ± 0.3% per 100 mV depolarizing step (Fig. 1_E_). The relative change in SHG is defined as:

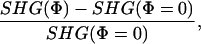graphic file with name M1.gif [1]

where Φ is the membrane potential. As opposed to SHG, the two-photon fluorescence of the same pixels did not show any modulation with voltage (data not shown). Also, neurons that were not patched did not show any corresponding modulation in SHG intensity (data not shown).

We then switched to perform SHG measurements from neurons in brain slices. To increase the dye concentration in the membrane and be able to image dendritic spines, we loaded FM 4-64 dye intracellularly by a patch pipette in pyramidal neurons from mouse hippocampal and neocortical slices. After 30 min, the dye diffused far beyond the soma (Fig. 2_A_), and apical and basal dendrites, including dendritic spines, were clearly resolved (Fig. 2 A Inset). As with cultured cells, we examined the voltage sensitivity of SHG in intracellularly loaded cells by measuring SHG signals from the somata of patched neurons during voltageclamp protocols with a slow frame acquisition (≈1 s per frame). In 16 experiments on 12 cells, we found that the SHG response for the cell soma was on average 11.9 ± 0.8% per 100 mV (at 900 nm excitation). An estimate of the noise was obtained from three series of experiments (four frames each) taken at a constant voltage. The coefficient of variation (SD divided by the mean) was 2.8 ± 0.8%. By using ≈3% frame to frame variability in the SHG intensity, we estimate the signal-to-noise (S/N) to be ≈4 for a voltage step of 100 mV. Again, simultaneously measured two-photon fluorescence signals (Fig. 2_B_) did not show any modulation by voltage (Fig. 2_C_).

Fig. 2.

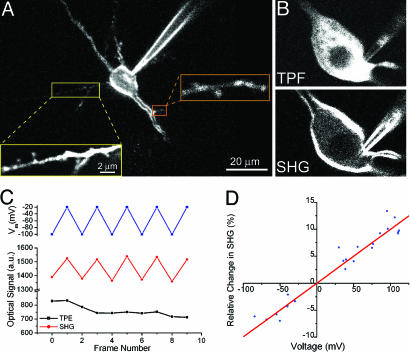
Fig. 2.

SHG imaging of neurons in brain slices with FM 4-64. (A) SHG image of pyramidal neuron in layer 5 of mouse primary visual cortex stained intracellularly with FM 4-64. Spines on basal dendrite and oblique dendrite can be readily seen. (B) Comparison between membrane contrast imaged with TPF and SHG of the same neuron. Notice the strong fluorescence signal originating from the cytoplasm. (C) SHG signal voltage sensitivity with framescan. A neuron was voltage-clamped, and movies were taken with command voltage switched in alternate frames. SHG, TPF intensity, and membrane voltage were plotted vs. frame number. The difference in intensity between the high and low voltages was very significant for the SHG data (P < 0.01, n = 5, t test) but not statistically significant for TPF data (P = 0.86, n = 5). The SHG response for the soma as a whole was 12.5 ± 0.6% per 100 mV (R = 0.991). (D) Characterization of SHG signal voltage sensitivity with pointscan. SHG signals were measured upon various current injection, and the resulting changes in SHG signal intensity were plotted against voltage changes recorded simultaneously by current-clamp recording (n = 23 from eight neurons). The linear regression through the origin revealed the SHG response to be 9.96% per 100 mV (R = 0.97).

Somatic SHG Responses to Fast Voltage Transients. Because the membrane potential dynamics under physiological stimulations are fast (ms time scales), we established a different imaging protocol, in which the laser beam remained focused at the selected target point (“pointscan”; see Materials and Methods). This method enabled us to monitor the SHG in one point with 0.1 ms temporal resolution, although extensive averaging (≈40 trials per point) were necessary to obtain sufficient S/N levels. We were concerned that, at these faster temporal resolutions, it is possible that the SHG voltage dependency could be substantially different compared with a slower framescan method. We therefore also calibrated the SHG of the pointscans with both depolarizing and hyperpolarizing somatic current injections (Fig. 2_D_). As with the slower measurements, pointscan data indicated that SHG is linear with voltage (9.96%/100 mV, R = 0.97) and changed signs at the zero voltage crossing. Both results are telltale signs of an electro-optic effect (25). Moreover, the slope of the voltage sensitivity with pointscans was similar to that obtained with framescans, indicating that the electro-optic mechanism was likely the same. The coefficient of variability of this measurement as defined above was 2.4 ± 0.7% (n = 4), with a S/N value of ≈4 for a voltage change of 100 mV. In addition, for intracellularly applied dye, SHG signals increased upon depolarization and decreased by hyperpolarizing the neuron, i.e., showing opposite polarity to the response of extracellularly loaded neurons (compare Fig. 1_E_ and 2 C and D). This reversed polarity is expected because, in the case of extracellular loading, the dye molecules should decorate the outer leaflet of the membrane's lipid bilayer (see Mathematical Methods). Although the electric field set by the resting membrane potential was always in the same direction (pointing toward the cytoplasm), the direction of the charge transfer in the dye molecule (and therefore the induced dipole moment) is reversed from the situation when the dye is at the inner leaflet. Thus, SHG response to a depolarizing step should have the opposite sign, but similar sensitivity. This result also indicates that the response is predominately electro-optic in nature rather than a reorientation effect (25).

SHG Response Calibration at Dendritic Spines. Because the biophysical properties of the spine membrane are still unknown, to establish that the chromophore behavior and SHG voltage sensitivity of spine membranes were similar to those of somatic and dendritic membranes, we performed experiments with intracellular Cs+ perfusion. This manipulation blocked K+ channels in the neuron, making the cell electrically more compact. In addition, we applied QX-314 (Alomone Laboratories, Jerusalem) (internally) and NiCl2 (externally) to block Na+ and Ca2+ channels, respectively. Using the same voltage-clamp protocols as used in the soma, we monitored the spine SHG and found that SHG signals from spines showed indistinguishable sensitivity to that of parent dendrites (SHG signal change at spines normalized to that of parent dendrites: 0.99 ± 0.09, P = 0.7, n = 5, Fig. 3_C_). These measurements assured us that the SHG signals from the spines could be interpreted with the same calibration scale and biophysical mechanisms as the somatic ones. Therefore, we used the calibration scale obtained from somatic pointscan measurement (9.96%/100 mV) in estimating voltage changes in spines in the following measurements.

Fig. 3.

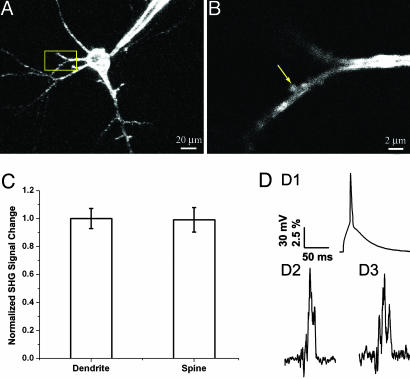
Fig. 3.

SHG measurements of spines during AP invasion. Representative layer 5 pyramidal neuron used for AP measurement by FM 4-64 SHG. (A)A _z_-stack of low-resolution image. (B) High-resolution image of the dendritic spine on the basal dendrite marked in A. (C) Calibration of spine SHG signals under voltage-clamp condition. Normalized SHG signal changes upon voltage steps at spines and their parent dendrites are shown. There are no significant differences between the sensitivity of SHG at spines and dendrites (P = 0.7, n = 5, t test). (D) SHG measurements during APs. A single AP was initiated by current injection at soma (shown in D1), and the resulting SHG signal changes were measured at soma (D2) and dendritic spines (D3). D2 and D3 are the average traces of four and seven recordings, with each recording as a result of averaging ≈40 APs, respectively.

SHG Measurements of Action Potentials (APs) in Somata and Spines. To demonstrate the ability of SHG to image fast neuronal membrane potential at high temporal resolution, APs were evoked at cell somata by current injection through the patch pipette and recorded optically. Pointscan averaging (≈40 stimulus presentations per point) showed good correspondence of SHG and recorded membrane potential change at soma (Fig. 3 D1 and D2) in current-clamp configuration with S/N ≈ 4.

We then turned our attention to image AP responses of spines. For these experiments, we focused exclusively on spines located on basal dendrites of layer 5 pyramidal neurons from mouse primary visual cortex, a population of spines electrotonically very close to the soma, which we have previously investigated anatomically and functionally (26, 27). When APs were generated at the soma, we imaged a corresponding increase in SHG at the head of the spine (Fig. 3_D3_). These increases were instantaneous with the somatic voltage deflections and had similar risetime and decay times as the voltage signal (Fig. 3_D1_). In fact, SHG signals at spine heads generated by APs were indistinguishable in amplitude and kinetics from SHG signals measured at the soma under identical protocols (spine, 10.8 ± 1.4%; soma, 11.1 ± 0.9%; n = 15 for spines and n = 17 for somata; S/N ≈ 3.5). These measurements required extensive averaging and showed large variability from spine to spine (Fig. 4). Because of the low S/N, we cannot ascertain whether this variability represents true biological variability.

Fig. 4.

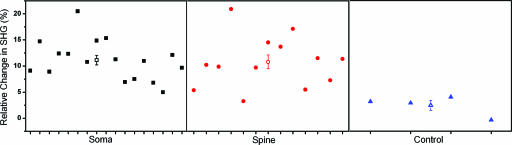
Fig. 4.

SHG measurements of membrane potential at somata and spines. Shown are peak SHG changes during APs for somata (black boxes), spines (red circles), and somata from control cells without APs (blue triangles) with mean and SE of the measurements (black open box, somata; red open circle, spines; blue open triangle, control somata). Each point represents measurements from a different neuron. The average SHG signal at spines during APs is not statistically different from that of somata (P = 0.8), but is different from control measurements (P < 0.01).

We conclude that single backpropagating APs invade the head of the dendritic spine without any substantial decrement in voltage or major electrical filtering. This result is in principle consistent with passive cable models, which have highlighted the electrical impedance mismatch between the dendrite and the spine, which should enable the efficient propagation of electrical pulses into the spines from the dendrites (5, 7). At the same time, it is possible that the electrical structure of the spine could be very different from that assumed by passive cable models so it seems pertinent to be cautious in the further interpretation of our measurements.

In summary, our results demonstrate that optical measurements of membrane potential in spines are possible and that the mechanism of voltage sensitivity of FM 4-64 SHG is electro-optic in nature and similar regardless of whether the chromophore is adsorbed to the somatic or spine plasma membrane. We also show that back-propagating APs invade most spines without significant voltage attenuation. Although passive electrotonic invasion of the spine by APs could occur, it is also possible that spines have Na+ channels and themselves produce regenerative spikes. Further experiments are needed to address the exact mechanisms of this AP invasion, as well as the behavior of spines under synaptic stimulation conditions. Finally, because spines are very heterogeneous in their structure and in some of their functions (1, 28, 29), it is possible that a different population of spines, or spines from a different cell type, could behave very differently.

Materials and Methods

Sample Preparation and Electrophysiology. Neuronal culture preparations are described in ref. 20. Acute coronal slices of 300 μm thickness were made from P13–P16 C57BL/6 mice by using a Vibratome (Leica VT1000S, Leitz, Vienna) in ice-cold cutting solution containing 222 mM sucrose, 27 mM NaHCO3, 2.6 mM KCl, 1.5 mM NaH2PO4, 0.5 mM CaCl2, and 7 mM MgSO4, bubbled with 95% O2/5% CO2 to pH 7.4. Slices were then transferred to a heated solution (37°C) containing 126 mM NaCl, 3 mM KCl, 1.14 mM NaH2PO4, 26 mM NaHCO3, 3 mM CaCl2, 1 mM MgSO4, and 10 mM dextrose, bubbled with 95% O2/5% CO2 to pH 7.4, for 0.5–1 h before being cooled to room temperature and used 6–10 h after slicing. All recordings from pyramidal neurons were made in whole-cell patch-clamp configuration (Dagan Amplifier BVC-700) at 25–37°C, by using patch pipettes (4–8 MΩ) that contained 135 mM KMeSO4, 5 mM NaCl, 10 mM KCl, 2.5 mM Mg-ATP, 0.3 mM Na-GTP, and 10 mM Hepes at pH 7.3. For Cs-based internal solution, the solution was changed to 110 mM cesium-gluconate, 20 mM CsCl, 2 mM EGTA, 10 mM Hepes, 0.3 mM Na-GTP, 1 mM Mg-ATP, and 5 mM QX-314, pH 7.3. In brain slices, when loading the cells intracellularly, we added 0.2–1 mM FM 4-64 dye (Biotium, Hayward, CA) to the internal solution. In culture, cells were loaded extracellularly with 50 μM FM 4-64.

Imaging. SHG imaging was performed by using a custom-made two-photon laser scanning microscope (30) with an Nd:glass laser at 1,064 nm (IC-100; HighQ Laser, Hohenems, Austria) or a Ti-Sapphire laser (Chameleon; Coherent, Santa Clara, CA) tuned to 900 nm. The illumination power of two lasers was independently modulated by Pockels cells [Conoptics (Danbury, CT) 350-50, and Quantum Technology (Lake Mary, FL) 327] with typical power of 1–10 mW on the sample. SHG signals were collected with a photomultiplier tube (H7422P-40; Hamamatsu, Hamamatsu City, Japan) after narrow band-pass filters (530/20 for 1,064 nm and 450/20 for 900 nm) and analyzed directly (for pointscan) or with FluoView (Olympus, Melville, NY) (for framescan). For framescan imaging, the laser raster scanned the sample with pixel dwell time of 6.4 or 16 μs. Pointscan experiments were performed by illuminating a laser at a target position for ≈40 times at 2 Hz each 30 ms, with simultaneous current injection in every other cycle, with no apparent photo-bleaching. Data were analyzed by custom written software by using matlab (Mathworks, Natick, MA). Averaged SHG signals from control and stimulation conditions were calculated with 2 ms of window-smoothing filtration and used to calculate the percentage of changes in SHG signals. All data are reported as mean ± SEM.

Mathematical Methods. Following is a brief description that accounts for both the linear dependence of the SHG _I_2ω, on the potential Φ across the membrane, and the opposite polarity of _I_2ω vs. Φ when the chromophore is at the extracellular vs. intracellular side of the membrane. The light at frequency ω incident on the membrane induces a nonlinear polarization, which generates the second-harmonic (SH) field _E_2ω at 2ω. It can be written as

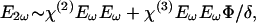graphic file with name M2.gif [2]

where χ(2) and χ(3) are the second and third order susceptibilities and _E_ω is the amplitude of the incident electric field. δ is the plasma membrane thickness, which is a constant and is omitted in the following derivations for simplicity. The observed SH _I_2ω is then given by

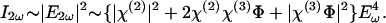graphic file with name M3.gif [3]

The second order term χ(2) is much larger than the higher order χ(3)Φ. Consequently, the |χ(3)Φ|2 is much less than χ(2)χ(3)Φ and can be neglected. In this way, we obtain

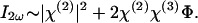graphic file with name M4.gif [4]

The linear dependency of _I_2ω on the potential Φ is directly seen. If we now consider the polarity dependence on the location of the chromophore, we note that it has the opposite orientation when located inside vs. outside because of symmetry. It therefore follows that χ(2) has the opposite sign at the two locations. For the dye loaded inside, as Φ increases, the relative SHG increases (Fig. 2_D_), whereas the relative SHG becomes negative for negative Φ. For the dye on the opposite side, χ(2) is opposite in sign. For positive Φ, the relative SHG is negative; for negative Φ, it is positive (Fig. 1_E_). This result is precisely what we observed.

Acknowledgments

We thank V. Nikolenko for the cultures and other members of the laboratory for comments. R.Y. is supported by the National Eye Institute, the Binational Science Foundation (U.S. and Israel), and the Human Frontier Science Program. K.B.E. is supported by the National Science Foundation.

Conflict of interest statement: No conflicts declared

Abbreviations: EPSP, excitatory postsynaptic potential; SHG, second harmonic generation; AP, action potential; S/N, signal-to-noise; TPF, two-photon excitation fluorescence.

Footnotes

Rall, W. & Rinzel, J. (1971) Soc. Neurosci. Abstr. 1, 64.

References