Cellular scaling rules for rodent brains (original) (raw)
Abstract
How do cell number and size determine brain size? Here, we show that, in the order Rodentia, increased size of the cerebral cortex, cerebellum, and remaining areas across six species is achieved through greater numbers of neurons of larger size, and much greater numbers of nonneuronal cells of roughly invariant size, such that the ratio between total neuronal and nonneuronal mass remains constant across species. Although relative cerebellar size remains stable among rodents, the number of cerebellar neurons increases with brain size more rapidly than in the cortex, such that the cerebellar fraction of total brain neurons increases with brain size. In contrast, although the relative cortical size increases with total brain size, the cortical fraction of total brain neurons remains constant. We propose that the faster increase in average neuronal size in the cerebral cortex than in the cerebellum as these structures gain neurons and the rapidly increasing glial numbers that generate glial mass to match total neuronal mass at a fixed glia/neuron total mass ratio are fundamental cellular constraints that lead to the relative expansion of cerebral cortical volume across species.
Keywords: allometry, brain size, comparative neuroanatomy, number of glia, number of neurons
Brain size varies by a factor of ≈100,000 across mammalian species (1, 2), and, although the cellular composition of the brain is one of the major determinants of its computational capacities (3), little is known about how the cellular composition varies with brain size. What are the cellular scaling rules that determine brain allometry? How do numbers of neuronal and nonneuronal cells contribute to structure size? What are the relative contributions of these cells across species of different brain sizes?
Glia are said to be the most numerous cell type in the brain (4, 5) and to be 10–50 times more numerous than neurons in humans (6). Evidence for this assertion, however, is scant. The ratio between the total number of glial and neuronal cells (glia/neuron ratio) in the cerebral cortex has been shown to increase with brain size (1, 7). However, the numeric expansion of glial cells relative to neurons seems to contradict the observation that the neuronal need for metabolic support remains similar across species (8). Data on how neuronal and glial cell sizes scale with brain size might help solve this discrepancy, but such data are lacking in the literature.
Not much is known, either, about the total numbers of neuronal and nonneuronal cells in the brains of different species, because methodological limitations have largely restricted comparative studies of brain anatomy to analyses of volumetric data published by a small number of laboratories. Strikingly, analyses of the same data yield conflicting conclusions. For instance, although the neocortical fraction of brain volume increases from 14% in basal insectivores to 80% in humans (9), the cerebellar fraction varies little across individuals of different mammalian orders (10), a discrepancy that the latter authors take to argue against the hypothesis that the cerebellum works in service of the neocortex. However, cerebellar and cerebral cortices increase concertedly in both surface area (11) and volume (12), parameters used in the literature to indicate computational capacity, and this evidence has been taken to suggest a functional dependence of one structure on the other. A conciliatory view holds that the cerebellum and neocortex evolved together but with the cerebellum evolving more slowly than the neocortex (12).
These conflicting interpretations demonstrate that cortical volume and surface, although informative measurements and widely used in the literature, particularly in relation to intelligence, cognitive abilities, and versatility (13–15), are only indirect indicators of computational capacity. A comparison of direct estimates of numbers of neurons in these structures might be a better tool to clarify the issue of how cerebral and cerebellar cortices are structurally and functionally related.
Here, we use the isotropic fractionator (16), a nonstereological method, to determine total numbers of neuronal and nonneuronal cells in the cerebral cortex, cerebellum, and remaining areas of the brain and to examine how they scale across six species of the same order, Rodentia, from mouse to the giant Amazonian capybara.
Results
Across the six rodent species we studied, body mass varies >1,000-fold, from ≈40 g in the mouse to >40 kg in the capybara, whereas brain mass varies by a factor of <200, accompanied by a smaller increase of 45 times in total number of cells, and an even smaller 22-times increase in the total number of neurons (Table 1). We find that body mass (MBO) in adult individuals relates to total brain mass (MBR) by a power function, such that MBR ≈ MBO0.773 (see Fig. 5, which is published as supporting information on the PNAS web site), in accordance with observations in rodents (17) and other mammalian orders (18), reporting that body size increases faster than brain size in phylogeny. Total brain mass also increases as a power function of the total number of cells (NC) in the brain of these species (MBR ≈ NC1.323) and can be expressed as a steeper power function of the total number of neurons with exponent 1.587.
Table 1.
Comparative cellular composition of the brains of six rodent species
| Species | Body mass, g | Brain mass, g | Total cells (×106) | Total neurons (×106) |
|---|---|---|---|---|
| Mouse | 40.4 ± 11.6 | 0.416 ± 0.028 | 108.69 ± 16.25 | 70.89 ± 10.41 |
| Hamster | 168.1 ± 13.6 | 1.020 ± 0.147 | 166.12 ± 23.77 | 89.97 ± 9.55 |
| Rat | 315.1 ± 102.9 | 1.802 ± 0.313 | 331.65 ± 8.84 | 200.13 ± 12.17 |
| Guinea pig | 311.0 ± 49.1 | 3.759 ± 0.499 | 477.87 ± 10.57 | 239.62 ± 2.79 |
| Agouti | 2,843.3 ± 195.5 | 18.365 ± 2.061 | 1,941.46 ± 65.81 | 856.74 |
| Capybara | 47,500.0 ± 3,535.5 | 76.036 ± 3.787 | 4,866.44 ± 1,080.76 | 1,601.12 ± 81.16 |
| Variation | 1,176-fold | 183-fold | 45-fold | 22-fold |
Fractional Distribution of Cells and Neurons.
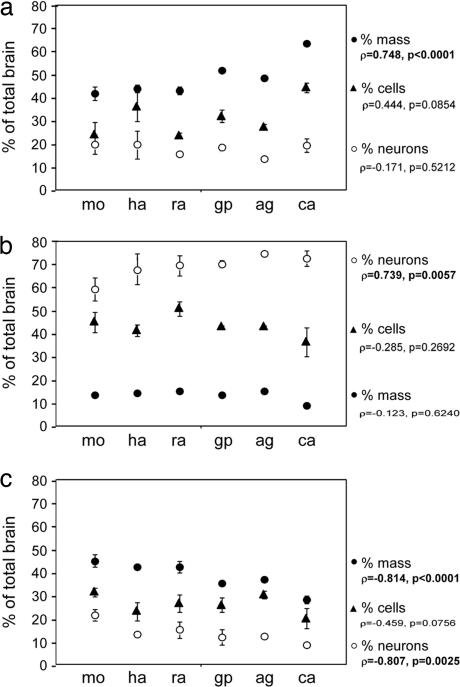
The relative size of the cerebral cortex, expressed as the fraction of brain mass contained in this structure, increases significantly with brain size in these rodent species, whereas relative cerebellar mass remains constant, and relative mass of the remaining structures decreases, as described in the literature (10, 19) (Fig. 1). Interestingly, the fraction of neurons contained in each of these divisions behaves differently: Regardless of total brain size, the cerebral cortex in all six species contains a relatively stable 17.8 ± 3.4% of all brain neurons (Fig. 1a, ρ = −0.171; P = 0.5212, Spearman rank correlation). In contrast, larger cerebella hold increasing fractions of total brain neurons, from 59.0 ± 5.0% in the mouse to 72.4 ± 3.3% in the capybara (Fig. 1b, ρ = 0.739; P = 0.0057), whereas the fraction of total brain neurons contained in the remaining areas decreases with increasing brain size (Fig. 1c, ρ = −0.807; P = 0.0025). These data suggest that different neuronal scaling rules apply to the cerebral cortex, cerebellum, and remaining brain structures.
Fig. 1.
Percent mass (filled circles), cells (filled triangles), and neurons (open circles) contained in the cerebral cortex (a), cerebellum (b), and remaining areas (c) relative to the whole brain in each species, arranged by increasing brain size. Bars indicate SD. Spearman correlation coefficients (ρ) and P values are indicated. mo, mouse; ha, hamster; ra, rat; gp, guinea pig; ag, agouti; ca, capybara.
Structure Size as a Function of the Number of Neuronal and Nonneuronal Cells.
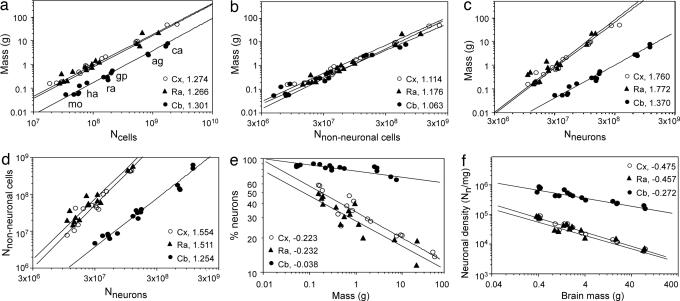
We next assessed cellular scaling rules for these three brain divisions by examining how tissue mass covaries with NC across species. Tissue mass varies as a power function of total NC (Fig. 2a) and of the number of nonneuronal cells (Fig. 2b, NNN), with similar exponents for the cerebral cortex, cerebellum, and remaining areas. In contrast, the mass of the cerebral cortex (MCX) and that of remaining areas (MRA) increase more steeply than cerebellar mass (MCB) as a power function of their respective numbers of neurons (Fig. 2c, NN). This difference is simultaneous with the addition of greater numbers of nonneuronal cells to the cerebral cortex and remaining areas than to the cerebellum as these structures gain neurons (Fig. 2d). The latter finding is also evident as a prominent decrease in the percentage of cells that are neurons (and presumably as an increase in the glia/neuron index) with increasing mass of the cerebral cortex and remaining areas but not so prominent for the cerebellum (Fig. 2e).
Fig. 2.
Cellular scaling rules for rodent brains. Each point represents one individual. Species are as indicated in a. All graphs are fitted with power functions whose exponents are indicated. All P < 0.0001. (a_–_c) Graphs show structure mass across species as a function of total number of cells (a), total number of nonneuronal cells (b), and total number of neurons (c). (d) Total number of nonneuronal cells as a function of total number of neurons in each structure across species. (e) Percentage of neurons relative to total number of cells in each structure as a function of total brain mass across species. (f) Neuronal density as a function of total brain mass for each structure, across species. Cx, cerebral cortex; Cb, cerebellum; Ra, remaining areas; mo, mouse; ha, hamster; ra, rat; gp, guinea pig; ag, agouti; ca, capybara.
Cell Densities.
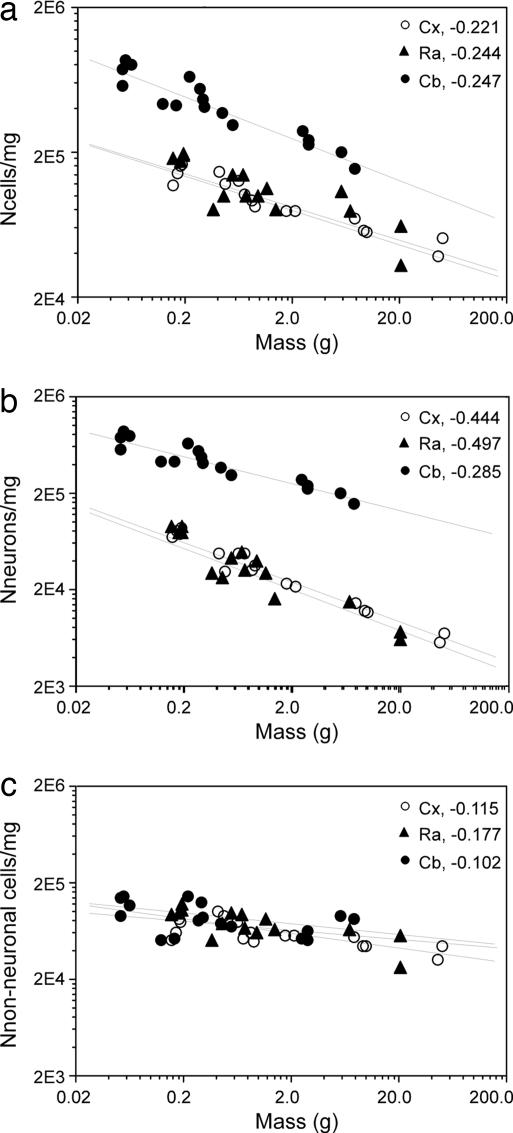
As expected from the larger increase in brain mass than in the number of neurons, neuronal density decreases in these six rodent species as a power function of brain size with an exponent that is slightly more negative than those found in the literature (1, 20, 21) and at rates that are similar in the cerebral cortex and remaining areas and larger in these than in the cerebellum (Fig. 2f). Separate analysis of total cellular and neuronal densities shows that similar values are found for the cerebral cortex and remaining areas of equivalent mass, and densities scale with structure mass, with exponents that are similar for the two structures (Fig. 3a). The cerebellum is distinctive in that it has larger cellular and neuronal densities than the cerebral cortex or remaining areas of equivalent mass, and cerebellar neuronal density scales less steeply than that of the other structures (Fig. 3b). Remarkably, the cerebellum, cerebral cortex, and remaining areas share similar nonneuronal cell densities, which vary very little with structure size (Fig. 3c). These findings suggest that the addition of nonneuronal cells follows the same principle and contributes equally in all structures and species toward final structure size.
Fig. 3.
Variation in total (a), neuronal (b), and nonneuronal (c) cell density in the cerebral cortex, cerebellum, and remaining areas as a function of structure mass. All graphs are fitted with power functions whose exponents are indicated. (a and b) All P < 0.0001. (c) P = 0.0009 (Cx and Cb); P = 0.0611 (Ra).
Neuronal density scales less steeply than neuronal number across brains of different sizes. Although the latter increases 23 times from the mouse to the capybara, neuronal density in all structures decreases by a factor <10-fold. An even more marked difference is observed for nonneuronal cells, whose 86-fold increase in number from the mouse to the capybara is accompanied by a modest decrease in nonneuronal cell density of ≈2-fold (see Table 2 and Supporting Appendix, which are published as supporting information on the PNAS web site). This difference in the steepness of scaling between neuronal and nonneuronal cells indicates that the latter vary much less in size than do neuronal cells across species, a possibility that we addressed next.
Relative Contribution of Neuronal and Nonneuronal Cell Size to Brain Mass.
Methodological limitations make difficult the direct measurement of cell sizes across species, but a mathematical analysis offers initial estimates of how neuronal and nonneuronal cell size scales as a function of cell number. If the mass of any given cell is considered to include all cellular processes and surrounding extracellular space, then the mass of any brain division can be expressed as the product of NC and the average cell mass (MC). We observe that MC increases in the cerebral cortex, cerebellum, and remaining areas as similar power functions of NC·cx, NC·cb, and NC·ra (slope β = 0.274, 0.301, and 0.266, respectively; see Methods).
Other groups have shown that neuronal density (1, 20, 21) scales with brain mass, and our observation that it also scales directly as a power function of number of neurons suggests that neuronal size, as defined above, also scales with neuron number. Indeed, neuronal cell size and soma volume are known to scale as functions of brain mass (1, 20–22) and, thus, presumably, as we show, with the number of neurons. Assuming, therefore, that the average neuron (MN) and nonneuronal (MNN) cell mass scale as power functions of NN and NNN, respectively, their relative contributions to the total size of each structure can be estimated mathematically (see Methods). Our data suggest that average neuronal size increases as similar functions of NN in the cerebral cortex and remaining areas (β = 0.760 and 0.772, respectively) and less rapidly with increasing NN in the cerebellum (β = 0.370). In contrast, average nonneuronal cell size is estimated to increase very little, and by similar exponents, as a function of NNN in all three structures (β = 0.114, 0.063, and 0.176 for the cerebral cortex, cerebellum, and remaining areas, respectively).
Interestingly, because we observe that NN and NNN are related by a power function, it can be demonstrated mathematically that the ratio between total neuronal (NN× MN) and total nonneuronal (NNN× MNN) mass for each structure, and for the whole brain, is constant among species, regardless of brain size (see supporting information).
Because structure mass scales as the product of variations in NN and MN, the relative contribution of these two variables (ΔNN/ΔMN) to the final size of any structure can be estimated as another power function of NN with exponent χ = 1 − β, yielding χN = 0.240 and 0.228 for cerebral cortex and remaining areas, respectively, and χN = 0.630 for cerebellum, where χ = 0 indicates similar relative contributions of neuronal number and average neuronal size, and χ = 1 indicates no contribution of average neuronal size. The coefficients obtained indicate that not only do changes in MN contribute less than changes in NN to final structure size but also that the larger the increase in NN between two species, the smaller the relative contribution of MN to final structure size, particularly for the cerebral cortex and remaining areas. When the same rationale is applied to nonneuronal cells, it is found that the relative contribution of NNN and MNN (ΔNNN/ΔMNN) to final structure size varies as a power function of NNN in the structures with larger exponents (χNN = 0.886, 0.937, and 0.824 for the cerebral cortex, cerebellum, and remaining areas, respectively). In contrast to the χN obtained, the larger values of χNN indicate that increasing numbers of nonneuronal cells are added to all three structures in the absence of large changes in average nonneuronal cell size.
Comparative Scaling of Cerebral Cortex and Cerebellum.
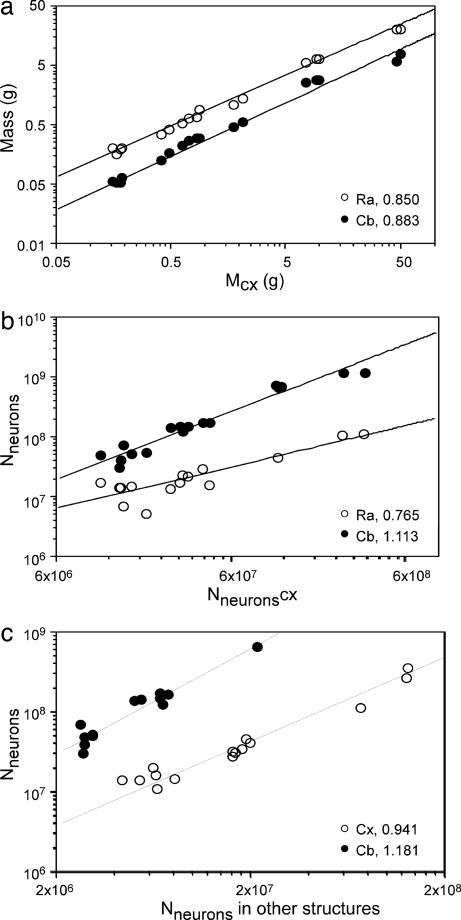
Direct comparison across structures shows that, whereas the cerebral cortex gains mass faster than the other structures (Fig. 4a), the total number of neurons increases more rapidly in the cerebellum than in the cerebral cortex and remaining areas (Fig. 4b), as could be expected from the fractional distribution of neurons across the cerebral cortex, cerebellum, and the remaining areas (Fig. 1). Whereas the total number of neurons in the cerebral cortex increases as a power function of the number of neurons in all other brain structures, with an exponent of 0.941 (P < 0.0001), the exponent relating the total number of neurons in the cerebellum to the number in all other brain structures is 1.181 (P < 0.0001) (Fig. 4c). Thus, although the cerebral cortex with the subjacent white matter increases rapidly in fractional volume and becomes the dominant brain structure in relative volume as overall brain size increases across species (10, 19), the cerebral cortex gains neurons, at most, isometrically with the remainder of the brain and maintains a constant fraction of all brain neurons. In contrast, the cerebellum, although maintaining a constant fractional volume of the brain, gains neurons faster than both the cerebral cortex and the remaining structures and encloses gradually larger fractions of all brain neurons as brain size increases.
Fig. 4.
Variation in mass (a) and total number of neurons (b and c) of cerebellum and remaining areas as a function of these values in the cerebral cortex (a and b) and in the other structures (c). Power function exponents are indicated. P < 0.0001 (a) and P = 0.0005 (b and c). Notice that, although cerebellar mass increases at a smaller rate than cerebral cortical mass, the total number of cerebellar neurons grows more rapidly than that in the cerebral cortex.
Discussion
The cellular scaling rules for rodent brains that we describe here indicate that larger brains are built with more neurons and even larger numbers of nonneuronal cells, particularly in the cerebral cortex and remaining areas; in addition, as their numbers increase, neurons increase in size, but nonneuronal cells maintain their average size relatively constant. Between mice and capybaras, we show that the 278-fold difference in mass of the cerebral cortex is due to a 22-fold increase in the number of neurons and a 154-fold increase in the number of nonneuronal cells. Given the power laws that relate cell number and average cell size, we estimate that the 22 times more numerous cerebral cortical neurons are, on average, 10 times larger in the capybara than in the mouse, whereas the 154 times more numerous nonneuronal cells are only 1.8 times larger. In the cerebellum, on the other hand, the 28 times more numerous neurons are, on average, only 3 times larger in capybara than in mouse, whereas the 82 times more numerous nonneuronal cells become, on average, only 1.3 times larger in the bigger rodent.
It will be interesting to see whether data on neuronal and nonneuronal cell size will match our estimates as they become available by direct measurement. According to our estimates, a rodent brain with a human-sized cerebellum would be expected to have ≈900 times more cerebellar nonneuronal cells that are, on average, only 1.5 times larger than in the mouse cerebellum. Recent measurements of human astrocytes have shown that they are only 3 times larger than mouse astrocytes,§ which seems to be good evidence that nonneuronal cell size indeed changes very little with cell number. Similarly, Purkinje cells are 50 times more numerous in the human (24) than in the rat cerebellum (25) and would, therefore, be expected to be 4.2 times larger in the former, according to our estimates; in the literature, these cells have been found to have a 2.5 times bigger perykaryon (26), which falls close enough to the expected value, given that the arborizations were not considered in that study.
So far, we have been unable to analyze separate neuronal subpopulations. Although our estimates refer to the total population of neurons, the literature suggests that similar scaling laws apply to some aspects of different neuronal populations within each structure. For example, neuronal density scales in all three cerebellar layers, of strikingly different cellular compositions, as power functions of cerebellar weight with similar exponents, even though the ratio between numbers of granular and Purkinje cells changes (27). To the extent that the organization of both cerebral (28) and cerebellar (29) cortices is modular, with the same basic laminar, tangential, and connective organization throughout in columnar functional units along the surface, some aspects of cellular allometry can be expected to scale at similar rates among neuronal subtypes as more modules are added, and it will be informative to determine which aspects do and which do not.
Our data suggest that cell number and mass are regulated in such a way that the ratio between total neuronal and total nonneuronal mass is kept constant in the brain, even though the glia/neuron index increases along with brain mass (30, 31). This finding means that the significant increase in neuronal size as the number of neurons increases is compensated by the addition of much larger numbers of nonneuronal cells of only slightly larger size, such that a 2-fold increase in total neuronal mass is accompanied by an equal 2-fold increase in total nonneuronal mass and yields a 2-fold increase in brain size. The overall mass constraint suggested by our data is compatible with the recent notion that glial cells serve as dynamic regulators of neuronal production, function, and phenotype and organize brain tissue into functional compartments (8). On the other hand, an increase in the number of glial units would favor a growing participation of these cells in neural computation, as has been proposed recently (32, 33), without compromising their role in regulatory and support functions. The constant neuronal/nonneuronal mass ratio also settles the apparent discrepancy between the numeric expansion of glial cells compared with neurons, whereas the neuronal need for metabolic support remains similar across species (8). Because increasing numbers of neurons result in larger brain size, these neurons can be expected to increase in size, with not only larger somata but, particularly, longer processes to maintain long-distance connectivity as brain size increases. Compared with neurons, glial cells act locally, so as the brain grows, their sustained small size relative to increasingly larger neurons would be compensated by the addition of larger numbers of glial cells, thereby maintaining a constant balance between total neuronal and nonneuronal mass in the brain, which we propose to be a major mechanism in driving changes in brain size.
This constant balance could be achieved economically if the increased neuronal proliferation that has been proposed to drive cortical growth across species (34) led, during the development of each individual, to the generation of appropriate numbers of glial cells through the regulation of gliogenesis, which is largely postnatal (35), according to the number of neurons generated in each structure. Gliogenesis is known to be regulated by neuronal activity (31), and it has also been demonstrated that glial precursor proliferation is density-dependent and ceases once a steady-state glial density has been achieved, most likely by cell–cell contact inhibition (36). In this direction, it is remarkable that the three brain regions in all of the rodent species that we examined share similar nonneuronal cell densities, despite containing very different numbers of neurons, which is what one should observe if gliogenesis were regulated by contact inhibition among proliferating precursors and newly added glial cells as they invade structures that are, in early development, composed mostly of neurons. Thus, we suggest that continued gliogenesis until confluency is reached in a formerly purely neuronal tissue is a likely candidate mechanism by which neuronal and nonneuronal cell numbers are related and by which the ratio between total neuronal and nonneuronal mass could be kept constant across species. It will be interesting to estimate total neuronal and nonneuronal mass in different brain structures and see how manipulations of neuron number affect both the number and mass of nonneuronal cells.
Our data indicate another unexpected trend in cellular scaling of the brain, namely that the relative volumetric expansion of the cerebral cortex does not reflect a corresponding expansion of its number of neurons relative to the whole brain, because this relationship seems to be fixed at ≈18% in all species examined. In contrast, the stable relative cerebellar volume across species masks an increase in its relative number of neurons. We propose that this differential expansion of relative volume and number of neurons between the cerebral cortex and cerebellum has its origin in the larger increase in the average size of neurons in the cerebral cortex (a power function of exponent 0.760 of neuron number) compared with the increase in average cerebellar neuronal size (a power function of exponent 0.370 of neuron number), matched by a corresponding increase in total nonneuronal mass. This finding is in good agreement with the known architecture of cerebral and cerebellar cortices, the former composed of relatively large numbers of neurons with large cell bodies and extensively arborized processes that span long distances (28) and the latter composed mostly of much smaller neurons with a single, long, and comparatively local arborization (29). Along this line, it is interesting to note that the larger the increase in NN between two species, the smaller the relative contribution of MN to final structure size, particularly for the cerebral cortex and remaining areas, consistent with a strong selective pressure against increased neuronal size, lest the brain becomes too large too fast as it gains neurons (37).
Volume and surface measurements of the cerebral cortex and cerebellum have been widely used in the literature as indicators of the computational capacity of these structures (10–12), with the tacit assumption that they vary directly according to the number of neurons in these modular structures (28, 29), for instance, as more columns of a same total number of neurons are added (38). However, our results of a constant relative number of neurons in the cortex and an increasing number in the cerebellum show that changes in volume cannot be used as proxy for changes in number of neurons or of nonneuronal cells. As long as neurons are considered the functional integrative units of nervous tissue, inferences of computational power of brain structures should take their number into account, given that this should be a far more direct indicator of computational capacity than structure volume and surface, which are inflated in different ways by nonneuronal cells and connecting fibers of larger caliber. The total number of neurons should also be more direct an indicator of computational capacity than total neuronal mass, because increasing soma size, the extent of arborizations, and the number of synapses allows neurons to integrate more information but not to separate them as different computational units unless there were also more neurons in the brain. Clearly, however, the number of neurons in a structure is not the sole determinant of its computational capacity, because it must be combined with synaptic numbers and density, variables that we do not investigate here.
It could still be argued that the expected increase in computational power of larger cerebral cortices does relate to an increase in absolute number of neurons across species. However, this argument would have to be logically extended to the cerebellum, which is modular in its structure like the cortex. We find, nevertheless, that the cerebellum actually gains more neurons than does the cerebral cortex as these structures become larger in rodents, a finding that would, by extension, imply that the cerebellum actually gains computational power faster than the cerebral cortex as brains become larger.
It is important to realize that the current view of encephalization and neocorticalization as adaptive and selected traits in evolution (13) is based on volumetric relationships that we show not to hold at the cellular level of brain composition and, therefore, may not be reliable indicators of function. It is interesting to wonder how the view of neocorticalization would be different today if studies of cellular scaling rules had been available earlier. Given the increasing concentration of neurons in the cerebellum, perhaps we would instead deal today with concepts of cerebellarization of the brain. The notion that, from a neuronal point of view, the cerebellum might be favored with a greater increase in number of computational units than the cerebral cortex itself as both structures increase coordinately in size and in number of neurons is consistent with the newly recognized role of the cerebellum as a structure that accumulates sensory, motor, emotional, and cognitive functions, in addition to on-line error analysis on inputs derived from the cerebral cortex (18, 39).
Rather than its number of neurons, we find that the increased size of the cerebral cortex reflects more closely the changes in its total numbers of nonneuronal cells. In light of the recent discoveries on the functional contribution of glial cells to intercellular signaling, in concert with neurons (32, 33), this finding raises the possibility that it is the increasing numerical predominance of glial cells in the cerebral cortex that accounts for the expected increase in the computational power of larger brains.
In any case, given the discrepancies we show between the previous volumetric and the cellular scaling rules for rodent brains, our findings suggest that the cognitive and ecological significance of species differences in brain size should be reevaluated by examining directly the numbers of neuronal and nonneuronal cells and not just volume or surface area.
Methods
Animals.
Adult male Swiss mice (Mus musculus, n = 4), golden hamsters (Mesocrycetus auratus, n = 2), and Wistar rats (Rattus norvegicus, n = 4; data from this species appeared in a previous methods paper) (16) were bred at the colony at the Instituto de Ciências Biomédicas, Universidade Federal do Rio de Janeiro and were 2–5 months of age by the time of the experiments. Two young adult, 1-month-old male guinea pigs (Cavia porcellus) were supplied by Carlos Virgínio Codá (Rio de Janeiro). Three adult agoutis (Dasyprocta primnolopha, one female) and two adult female capybaras (Hydrochoerus hydrochoeris) of undetermined age were donated by the Federal University of Pará and the Brazilian Institute for Environmental Protection (IBAMA, Belém, Brazil), respectively.
Dissection.
All animals were killed by inhalation of ether, weighed, and perfused transcardially with 0.9% saline, followed by 4% phosphate-buffered paraformaldehyde. The brains were removed from the skulls by using the foramen magnum as the lower limit and dissected free of dura mater and superficial blood vessels, weighed, and postfixed for 2 weeks to 12 months by immersion in 4% phosphate-buffered paraformaldehyde. The cerebellum was dissected by cutting the cerebellar peduncles at the surface of the brainstem. The cerebral cortex in all animals was defined as all cortical regions lateral to the olfactory tract, including the hippocampus, and was dissected from each hemisphere by peeling the cerebral cortex away from the striatum and other subcortical structures under a stereomicroscope. All other brain structures, including the olfactory bulb, were pooled and processed together as “remaining areas.” In mice, hamsters, rats, and guinea pigs, the two hemispheres were counted together; in agoutis and capybaras, only one of the two hemispheres was processed, and results were multiplied by 2 to estimate numbers for the whole brain.
Isotropic Fractionator.
Total numbers of cells, neurons, and nonneuronal cells were estimated as described by using the isotropic fractionator method (16). Briefly, each dissected brain division is turned into an isotropic suspension of isolated nuclei of known, defined volume, kept homogeneous by agitation. The total number of nuclei in suspension and, therefore, the total number of cells in the original tissue, is estimated by determining the density of nuclei in small aliquots stained with the fluorescent DNA marker DAPI (4′-6-diamidino-2-phenylindole dihydrochloride) under the microscope. Once the total cell number was known, the proportion of neurons was determined by immunocytochemical detection of neuronal nuclear antigen (NeuN), expressed in all nuclei of most neuronal cell types and not in nonneuronal cells (23, 40). Estimates of the proportion of NeuN-positive nuclei are considered reliable, because the coefficient of variation among animals of the same species is typically <0.15 (see supporting information). Numbers of nonneuronal cells are derived by subtraction.
Data Analysis.
All statistical analyses and regressions were performed in Statview (SAS, Cary, NC). Nonparametric Spearman rank correlations were calculated for fractional distributions of mass, number of cells, and number of neurons across species because there was no way to ascertain that the variables were normally distributed.
Estimates of Scaling of Average Cell Size.
Considering that total brain mass (MBR) can be expressed as the product of the total number of cells (Ncbr) and their average size (or mass, Mc), here considered to include all cellular processes and surrounding extracellular space, it is possible to estimate the relative contributions of cell number and average cell size to final brain mass. Because MBR = Ncbr × Mc, the slopes (β) of the power function Mc ≈ Ncβ for each structure can be inferred from the slopes (α) of the power functions relating M ≈ Ncα in Fig. 3, as β = α − 1.
Estimates of Scaling of Average Neuronal and Nonneuronal Cell Size.
The contributions of average neuronal (MN) and nonneuronal (MNN) cell mass to the total size of each structure can also be estimated by assuming that MN and MNN vary as power functions of neuronal (NN) and nonneuronal (NNN) cell number, respectively, which is warranted by estimates of changes in cell size with brain mass (1, 19, 20) and by the finding that neuronal density decreases with increasing brain mass (1, 20, 21). Based on this assumption, if M = NN × MN + NNN × MNN and the exponents α relating M ≈ NNα and M ≈ Nnnα are known, the slopes (β) of the power functions MN ≈ NNβ and MNN ≈ NNNβ can also be inferred from the slopes (α) in Fig. 3, as β = α − 1 (see supporting information).
Supplementary Material
Supporting Information
Acknowledgments
We thank Jean-Christophe Houzel [Universidade Federal do Rio de Janeiro (UFRJ)], Cristóvam Picanço-Diniz, Ivanira Dias, Carlomagno Bahia (Universidade Federal do Pará, Brazil), and the Instituto Brasileiro do Meio Ambiente for providing agouti and capybara specimens; Cristiano Nascimento Costa for help in some experiments; Adiel Nascimento for expert animal care; Elizabeth de Moraes and Antônia Lima Carvalho for technical assistance; Vivaldo Moura-Neto, Flávia Gomes, and José Garcia Abreu (UFRJ) for providing materials; and Robert H. Miller for bringing density-dependent gliogenesis to our attention. This work was supported by the Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro Primeiros Projetos and CNPq-PRONEX.
Footnotes
Conflict of interest statement: No conflicts declared.
§
Oberheim, N. E., Wang, X., Xu, Q., Takano, T. & Nedergaard, M. (2005) Soc. Neurosci. Abstr., abstr. 386.9.
References
- 1.Stolzenburg J. U., Reichenbach A, Neumann M. Glia. 1989;2:78–84. doi: 10.1002/glia.440020203. [DOI] [PubMed] [Google Scholar]
- 2.Tower D. B. J. Comp. Neurol. 1954;101:19–51. doi: 10.1002/cne.901010103. [DOI] [PubMed] [Google Scholar]
- 3.Williams R. W., Herrup K. Annu. Rev. Neurosci. 1988;11:423–453. doi: 10.1146/annurev.ne.11.030188.002231. [DOI] [PubMed] [Google Scholar]
- 4.Doetsch F. Nat. Neurosci. 2003;6:1127–1134. doi: 10.1038/nn1144. [DOI] [PubMed] [Google Scholar]
- 5.Nishiyama A., Yang Z., Butt A. J. Anat. 2005;207:687–693. doi: 10.1111/j.1469-7580.2005.00489.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kandel E., Schwartz J., Jessel T. Principles of Neural Science. 4th Ed. New York: McGraw–Hill; 2000. p. 20. [Google Scholar]
- 7.Hawkins A., Olszewski J. Science. 1957;126:76–77. doi: 10.1126/science.126.3263.76. [DOI] [PubMed] [Google Scholar]
- 8.Nedergaard M., Ransom B., Goldman S. A. Trends Neurosci. 2003;26:523–530. doi: 10.1016/j.tins.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 9.Frahm H. D., Stephan H., Stephan M. J. Hirnforsch. 1982;23:375–389. [PubMed] [Google Scholar]
- 10.Clark D. A., Mitra P. P., Wang S. S. Nature. 2001;411:189–193. doi: 10.1038/35075564. [DOI] [PubMed] [Google Scholar]
- 11.Sultan F. Nature. 2002;415:133–134. doi: 10.1038/415133b. [DOI] [PubMed] [Google Scholar]
- 12.Barton R. A. Nature. 2002;415:134–135. doi: 10.1038/415134a. [DOI] [PubMed] [Google Scholar]
- 13.Jerison H. J. Philos. Trans. R. Soc. London Ser. B. 1985;308:21–35. doi: 10.1098/rstb.1985.0007. [DOI] [PubMed] [Google Scholar]
- 14.Reader S. M., Laland K. N. Proc. Natl. Acad. Sci. USA. 2002;99:4436–4441. doi: 10.1073/pnas.062041299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sol D., Duncan R. P., Blackburn T. M., Cassey P., Lefebvre L. Proc. Natl. Acad. Sci. USA. 2005;102:5460–5465. doi: 10.1073/pnas.0408145102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Herculano-Houzel S., Lent R. J. Neurosci. 2005;25:2518–2521. doi: 10.1523/JNEUROSCI.4526-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fox J. H., Wilczynski W. Brain Behav. Evol. 1986;28:157–169. doi: 10.1159/000118700. [DOI] [PubMed] [Google Scholar]
- 18.Martin R. D. Nature. 1981;293:57–60. doi: 10.1038/293057a0. [DOI] [PubMed] [Google Scholar]
- 19.Stephan H., Frahm H., Baron G. Folia Primatol. 1981;35:1–29. doi: 10.1159/000155963. [DOI] [PubMed] [Google Scholar]
- 20.Haug H. Am. J. Anat. 1987;180:126–142. doi: 10.1002/aja.1001800203. [DOI] [PubMed] [Google Scholar]
- 21.Tower D. B., Elliot K. A. C. Am. J. Physiol. 1952;168:747–759. doi: 10.1152/ajplegacy.1952.168.3.747. [DOI] [PubMed] [Google Scholar]
- 22.Shariff G. A. J. Comp. Neurol. 1953;98:381–400. doi: 10.1002/cne.900980302. [DOI] [PubMed] [Google Scholar]
- 23.Gittins R., Herrison P. J. Brain Res. Bull. 2004;63:155–160. doi: 10.1016/j.brainresbull.2004.02.005. [DOI] [PubMed] [Google Scholar]
- 24.Andersen B. B., Korbo L., Pakkenberg B. J. Comp. Neurol. 1992;326:549–560. doi: 10.1002/cne.903260405. [DOI] [PubMed] [Google Scholar]
- 25.Korbo L., Andersen B. B., Ladefoged O., Moller A. Brain Res. 1993;609:262–268. doi: 10.1016/0006-8993(93)90881-m. [DOI] [PubMed] [Google Scholar]
- 26.Korbo L., Andersen B. B. Neuroscience. 1995;69:151–158. doi: 10.1016/0306-4522(95)00223-6. [DOI] [PubMed] [Google Scholar]
- 27.Lange W. Cell Tiss. Res. 1975;157:115–124. doi: 10.1007/BF00223234. [DOI] [PubMed] [Google Scholar]
- 28.Douglas R. J., Martin K. A. C. Annu. Rev. Neurosci. 2004;27:419–451. doi: 10.1146/annurev.neuro.27.070203.144152. [DOI] [PubMed] [Google Scholar]
- 29.Leiner H. C., Leiner A. L., Dow R. S. Behav. Brain Res. 1991;44:113–128. doi: 10.1016/s0166-4328(05)80016-6. [DOI] [PubMed] [Google Scholar]
- 30.Tower D. B., Young O. M. J. Neurochem. 1973;20:269–278. doi: 10.1111/j.1471-4159.1973.tb12126.x. [DOI] [PubMed] [Google Scholar]
- 31.Reichenbach A. Glia. 1989;2:71–77. doi: 10.1002/glia.440020202. [DOI] [PubMed] [Google Scholar]
- 32.Allen N. J., Barres B. A. Curr. Opin. Neurobiol. 2005;15:542–548. doi: 10.1016/j.conb.2005.08.006. [DOI] [PubMed] [Google Scholar]
- 33.Volterra A., Meldolesi J. Nat. Rev. Neurosci. 2005;6:626–640. doi: 10.1038/nrn1722. [DOI] [PubMed] [Google Scholar]
- 34.Rakic P. Trends Neurosci. 1995;18:383–388. doi: 10.1016/0166-2236(95)93934-p. [DOI] [PubMed] [Google Scholar]
- 35.Sauvageot C. M., Stiles C. D. Curr. Opin. Neurobiol. 2002;12:244–249. doi: 10.1016/s0959-4388(02)00322-7. [DOI] [PubMed] [Google Scholar]
- 36.Zhang H., Miller R. H. J. Neurosci. 1996;16:6886–6895. doi: 10.1523/JNEUROSCI.16-21-06886.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Harrison K. H., Hof P. R., Wang S. S. J. Neurocytol. 2002;31:289–298. doi: 10.1023/a:1024178127195. [DOI] [PubMed] [Google Scholar]
- 38.Rockel A. J., Hiorns R. W., Powell T. P. Brain. 1980;103:221–244. doi: 10.1093/brain/103.2.221. [DOI] [PubMed] [Google Scholar]
- 39.Andreasen N. C., O'Leary D. S., Cizadlo T., Arndt S., Rezai K., Boles Ponto L. L., Watkins G. L., Hichwa R. D. Proc. Natl. Acad. Sci. USA. 1996;93:9985–9990. doi: 10.1073/pnas.93.18.9985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mullen R. J., Buck C. R., Smith A. M. Development (Cambridge, U.K.) 1992;116:201–211. doi: 10.1242/dev.116.1.201. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information