A First-Generation Metric Linkage Disequilibrium Map of Bovine Chromosome 6 (original) (raw)
Abstract
We constructed a metric linkage disequilibrium (LD) map of bovine chromosome 6 (BTA6) on the basis of data from 220 SNPs genotyped on 433 Australian dairy bulls. This metric LD map has distances in LD units (LDUs) that are analogous to centimorgans in linkage maps. The LD map of BTA6 has a total length of 8.9 LDUs. Within the LD map, regions of high LD (represented as blocks) and regions of low LD (steps) are observed, when plotted against the integrated map in kilobases. At the most stringent block definition, namely a set of loci with zero LDU increase over the span of these markers, BTA6 comprises 40 blocks, accounting for 41% of the chromosome. At a slightly lower stringency of block definition (a set of loci covering a maximum of 0.2 LDUs on the LD map), up to 81% of BTA6 is spanned by 46 blocks and with 13 steps that are likely to reflect recombination hot spots. The mean swept radius (the distance over which LD is likely to be useful for mapping) is 13.3 Mb, confirming extensive LD in Holstein–Friesian dairy cattle, which makes such populations ideal for whole-genome association studies.
POPULATIONWIDE association studies using a high density of genetic markers are powerful means of identifying common genetic variants that underlie complex traits. To be useful, markers tested for association must be either the causal mutation or highly associated (in linkage disequilibrium) with the causal mutation. Linkage disequilibrium (LD) describes a situation in which some combinations of alleles of two or more different loci (haplotypes) occur more or less frequently within a population than would be expected by chance alone. Information on the structure of LD at the population level is crucial for interpreting and applying results of genomewide association studies. Furthermore such information is critical for the design of panels of optimally spaced markers for high-powered, comprehensive genomewide association studies while simultaneously minimizing cost and genotyping effort.
The extent and pattern of LD have been extensively studied in humans. The LD structure in humans has been found to be quite complex and shown to vary between populations (Maniatis et al. 2002; Altshuler et al. 2005; Hinds et al. 2005). To help understand LD structure, LD maps on a scale of LD units (LDUs) have been developed (Maniatis et al. 2002; Tapper et al. 2005). LD maps facilitate association mapping, extend the resolution of linkage maps, allow comparison across populations, and are useful to detect selective sweeps and other events of evolutionary interest. One LDU is the distance in kilobases over which LD is useful for gene mapping in a particular genomic region, where useful is defined as LD remaining within _e_−1 (37%) of its initial value (Morton et al. 2001). One LDU is also called a “swept radius.” This distance varies substantially across the chromosome, with some regions having very extensive LD (where one LDU spans a large physical distance) and other regions where LD breaks down quickly (where there is a high LDU per kilobase ratio) (Morton et al. 2001). The LDU scale in LD maps is analogous to the (centi)morgan scale of linkage maps. At marker densities that are sufficiently high to fully delimit the LD structure, LDU map distances are additive (Ke et al. 2004), another property shared with the linkage map. When the cumulative LDU distances are plotted against the physical map, a pattern of plateaus (reflecting regions of low haplotype diversity or “LD blocks”) and steps (that represent recombination hot spots or recombination events) emerges. The intensity of recombination is related to the height (increase in LDU) of the step. However, the correspondence between LD structure and recombination is distorted, to some extent, by other factors such as mutation, drift, and selection that operate over the many generations during which the pattern of LD is determined. To the extent that these phenomena are important, both the physical and linkage maps are unreliable guides to LD structure. LD maps also identify “holes” or gaps within which a greater marker density is required to fully determine the LD structure and therefore define the optimal spacing of markers for association mapping and positional cloning (Tapper et al. 2005).
There have been reports of extensive long-range LD in most livestock species, based on studies using a low density of markers, including dairy cattle (Farnir et al. 2000; Khatkar et al. 2006), beef cattle (Odani et al. 2006), sheep (McRae et al. 2002), pigs (Nsengimana et al. 2004), and horses (Tozaki et al. 2005). The initial observations with low-density marker coverage in cattle indicate extensive LD in different dairy cattle populations. Farnir et al. (2000) reported LD between syntenic markers extending over “several tens of centimorgans” for a Dutch Holstein population. Khatkar et al. (2006) estimated that useful LD in Australian Holstein–Friesians extends up to 18 Mb.
Most estimates of LD in livestock populations are based on microsatellite genotype data. However, LD between microsatellites in humans is known to extend over longer distances compared to single-nucleotide polymorphism (SNP)-based estimates of LD (Pritchard and Przeworski 2001). It is of interest to see if corresponding differences in the strength of LD also extend to cattle.
With the Bovine Genome Sequence Project currently underway, patterns of LD across the bovine genome can be investigated using high-density SNP markers. SNPs are generally more useful than microsatellites for LD studies because of their greater abundance throughout the genome (Snelling et al. 2005) and the ease and reduced cost at which large-scale genotyping experiments may be conducted (Hinds et al. 2005). Characterizing the empirical patterns of LD across the genome is important to enhance our understanding of the biological processes of recombination and selection in the bovine genome. Furthermore, an understanding of the genomic landscape of bovine LD and variation in recombination rate facilitates the efficient design and analysis of association studies and greatly improves inferences from DNA marker polymorphism data based on population studies.
The bovine chromosome 6 (BTA6) has been reported to carry important quantitative trait loci (QTL) for production traits in a number of dairy cattle populations (Khatkar et al. 2004). We developed a panel of high-density SNP markers spanning this chromosome. Here we report the development of an LD map for BTA6 using this panel of SNPs in Australian Holstein–Friesian cattle to provide a better understanding of LD structure along the chromosome from which we can make some tentative inferences about the bovine genome as a whole.
MATERIALS AND METHODS
DNA samples and selection of bulls:
Straws of semen from 433 Australian Holstein–Friesian bulls were used as the source of DNA. Bulls were selected on the basis of their breeding values for different milk production traits as described in the database of the Australian Dairy Herd Improvement Scheme (ADHIS) (http://www.adhis.com.au/), which presents Australian breeding values (ABVs) for sires used in the Australian dairy cattle industry. The selected bulls are from the extremes of the distribution for four different traits, namely Australian profit ranking (APR), kilograms of protein, fertility, and somatic cell count (SCC), but as a whole group this sample of 433 bulls represents an approximately normal distribution for production traits measured and reported in the ADHIS database. The inbreeding coefficients and coefficient of coancestry between these bulls were computed on the basis of pedigree information obtained from ADHIS and using FORTRAN programs in the PEDIG package of D. Boichard (http://dga.jouy.inra.fr/sgqa/diffusions/pedig/pedigE.htm). There are low levels of kinship and inbreeding (see supplemental figures at http://www.genetics.org/supplemental/). The mean kinship (coefficient of coancestry) is 0.012 ± 0.021, with 0 and 0.016 for the first and third quartiles, respectively. The mean inbreeding coefficient is 0.8%. For the purposes of this study, these values were assumed to be zero.
Extraction and amplification of DNA from semen samples:
Semen samples for the bulls were obtained from Genetics Australia (Bacchus Marsh, Victoria, Australia). Genomic DNA was extracted from straws of frozen semen samples by a salting-out method adapted from Heyen et al. (1997). As the yields of some genomic DNA per straw were very small (0.25–43 μg), all DNA samples were amplified using a whole-genome amplification (WGA) kit (Repli-G; Molecular Staging). All genotyping on this panel of DNA samples was carried out using WGA DNA. Quantification of the WGA DNA was performed using picogreen (Molecular Probes, Eugene, OR; Invitrogen, San Diego) and assayed on a Victor2 1420 Multilabel Counter (Perkin Elmer, Norwalk, CT).
Identification and source of SNPs:
A panel of 450 SNPs predicted to be on BTA6 was initially selected for genotyping across our dairy cattle sample. Most of these were in silico SNPs derived from the Interactive Bovine In Silico SNP (IBISS) database (Hawken et al. 2004; http://www.livestockgenomics.csiro.au/ibiss/) and the International Bovine Genome Sequencing Project (http://www.hgsc.bcm.tmc.edu/projects/bovine/), published SNPs from NCBI, and SNPs identified through targeted gene sequencing (supplemental Table 1 at http://www.genetics.org/supplemental/).
SNP genotyping:
We used the high-throughput SNP assay service provided by Illumina BeadLab service facility in San Diego (http://www.illumina.com/; Illumina, San Diego), using their randomly ordered BeadArray technology (Fan et al. 2003). The Illumina genotyping system is fluorescence based, where each homozygote generates a single color specific to the appropriate allele, while the heterozygote generates both colors. Genotypes are visualized as clusters, where each marker generates three clusters of results, one each for the homozygotes and one for the heterozygotes. The tighter and more distinct the clusters are, the more accurate the genotyping data. To ensure accurate genotyping calls, quality scores of the allele calls (gene call scores) are provided through this genotyping service (Fan et al. 2003).
Estimation of SNP locations on BTA6:
A draft version of the bovine genome sequence (Btau 2.0) is available (ftp://ftp.hgsc.bcm.tmc.edu/pub/data/Btaurus/fasta/Btau20050310-freeze). Although this assembly has good coverage and high base accuracy within contigs, it is of limited usefulness for the assignment of SNPs to chromosomes because of the large number of unanchored sequence scaffolds. Therefore, estimates of the positions of SNPs on BTA6 were based on a comparison of human (HSA4) and bovine (BTA6) genetic and physical maps. The human map used was the NCBI human genome reference sequence (NCBI35). The bovine map was a customized version of the integrated bovine map known as the bovine Location DataBase (bLDB) (http://medvet.angis.org.au/ldb/; Nicholas 2005). The bLDB, in which distance between markers is expressed in kilobases, is an integrated map constructed from all the major public-domain physical and genetic maps of cattle using the LDB software of Morton et al. (1992). This approach has previously been used for construction of an integrated human map before the completion of the human annotated sequence (Ke et al. 2001; Tapper et al. 2001) and was found to be reliable in both location and marker order compared with the full genome sequence (Tapper et al. 2001). The conserved blocks in which both gene content and order are highly conserved between HSA4 and BTA6 were identified by comparing the positions of all orthologs contained in the two maps. This was completed using the CMap (http://www.gramene.org/cmap/) visual interface to display a comparative view of BTA6 and HSA4 and then identifying nonoverlapping blocks of orthology. The positions of bovine SNPs used in this study were first calculated on the human map using BLAT (Kent 2002) similarity searching with the best hit retained as the definitive position. If a SNP lay within a conserved block it was then given a bovine map position by interpolation. Of the 220 SNPs placed on the bLDB this way, 132 could also be positioned on the BTA6 linearized scaffolds from Btau 2.0 using BLAT and the two estimates of location were found to be in reasonable agreement (data not shown).
Testing for Hardy–Weinberg equilibrium:
The number of alleles and the observed and expected heterozygosities under Hardy–Weinberg Equilibrium (HWE) were computed for each SNP using the web version of Genepop (http://wbiomed.curtin.edu.au/genepop). The _P_-values of Fisher's exact test for deviations from HWE were computed as per Guo and Thompson (1992) using Genepop.
Construction of metric LD maps:
We used the LDMAP program (http://cedar.genetics.soton.ac.uk/pub/PROGRAMS/LDMAP) described and developed by Maniatis et al. (2002) to construct LD maps from phase-unknown diplotypes. LDMAP first computes the absolute value of the _D_′-statistic (Lewontin 1964) for all pairs of markers. Next it fits the Malecot model (Malecot 1948; Maniatis et al. 2002) to _D_′ vs. intermarker distance (d) data in kilobases. This quantifies the average rate of decline of LD with distance over the whole chromosome, which is a useful starting value for computing the interval-specific estimates used in LD map construction.
The Malecot model predicts the decline of association with distance as ρ(d) = (1 − L)Me−_κ_d + L, with ρ(d) = E(D_′), and where L is the residual association at large distances, M is the proportion of the youngest haplotype that is monophyletic, and κ is the rate of exponential decline of ρ(d) with distance d. For LD map construction the LDMAP program estimates the Malecot κ-parameter in each map interval using data from marker pairs that include that interval in sliding windows. The length of the i_th interval is κ_idi LDUs, where κ_i is the Malecot decay rate parameter specific to that interval, and di is the length of the interval on the physical map in kilobases. A chromosome has a total of 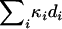 LDUs (Maniatis et al. 2002).
LDUs (Maniatis et al. 2002).
Morton et al. (2001) used 1/κ, the average decay rate on the kilobase scale, as the mean extent of useful LD for mapping, and termed it the (average) swept radius. However, wide local variations in the extent of useful LD are reflected in the LD map. Equal spacing of SNPs on the LDU scale is required for optimal coverage of a region, with the expectation that several markers spanning a range of frequencies will be required within each LDU to detect variants of unknown frequency.
Estimation of recombination density and LD density:
Common markers were first selected to ensure consistent order between the genetic linkage map (http://www.marc.usda.gov/) and the physical map (bLDB) (Nicholas 2005). A total of 57 markers had map locations on both cattle maps. From these 57 markers, the recombination density between all pairs of adjacent markers was calculated by simply dividing the distance between the markers in the genetic map (in centimorgans) by the distance between the markers on the bLDB map (in megabases). The numbers of LDUs were determined for each interval, to calculate the LD density (LDUs per megabase) in each interval. Alternatively, the numbers of LDUs were also calculated on regular intervals on a 2-, 5-, and 10-Mb scale. Recombination and LD density were then compared by simple correlation.
Identification of LD blocks:
We used the LDU scale to identify LD blocks as suggested by Tapper et al. (2003). Initially, we used the most stringent definition of blocks; i.e., blocks were formed by combining adjacent intervals with LDU widths of 0. We then examined less stringent definitions, namely by combining adjacent intervals with LDU widths no greater than 0.10, 0.20, 0.50, and 1.0 LDU.
RESULTS
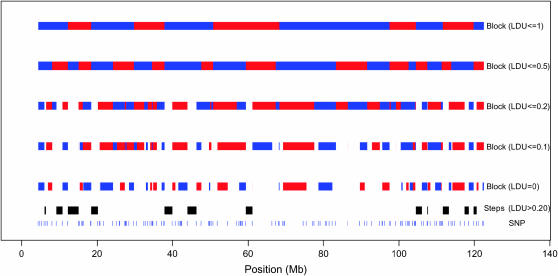
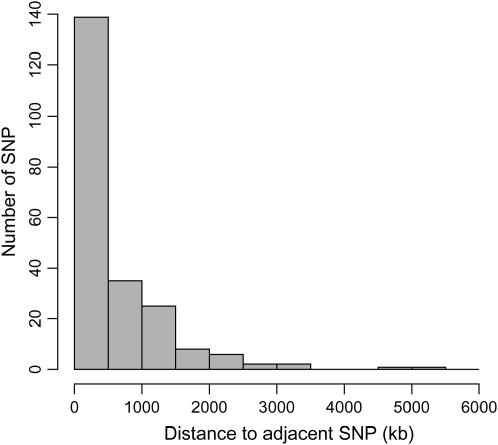
A total of 450 SNPs predicted to reside on BTA6 were selected for genotyping. Four hundred of these SNPs could be converted to a working assay (completed by Illumina BeadLab technology), and 315 were found to be polymorphic in our panel of 433 dairy bulls. For the purposes of this study, only SNPs with minor allelic frequencies (MAF) >0.1 were included in the analysis. All SNPs were tested for HWE and those that departed from HWE (P < 0.01) were also excluded. Furthermore, 8 SNPs showing disagreement of position between bovine sequence assembly (http://www.hgsc.bcm.tmc.edu/projects/bovine/) and the bLDB map (http://medvet.angis.org.au/ldb/) were excluded. Following these SNP screening procedures, genotyping data for 220 SNPs were used for final LD analysis. The location of these 220 SNPs on BTA6 is presented in Figure 1. Analysis of predicted positions and spacing of SNPs on BTA6 indicates 12 gaps of >2 Mb (maximal gap of 5.2 Mb; Figure 1), yielding a mean spacing of 539.2 kb and a median spacing of 192.5 kb (see Figure 2 for distribution of the spacing).
Figure 1.—
Location of SNPs, steps, and LD blocks on integrated map of BTA6. The SNP locations are shown at the bottom in blue. The LD blocks are shown in alternating red and blue at five different levels of stringencies. The steps are shown in black.
Figure 2.—
Distribution of SNP spacing: the distance in base pairs (kilobases) from one SNP marker to the next SNP marker on BTA6.
The mean MAF of the 220 SNPs was 0.29 (see supplemental figures at http://www.genetics.org/supplemental/), where 72% of SNPs had a MAF of >0.2, and 43.6% had a MAF of >0.3. The mean heterozygosity of these SNPs was 38.9% (see supplemental figures), 79.1% of SNPs had a heterozygosity of >30%, and a large proportion of SNPs showed a heterozygosity of >40% (47.3%).
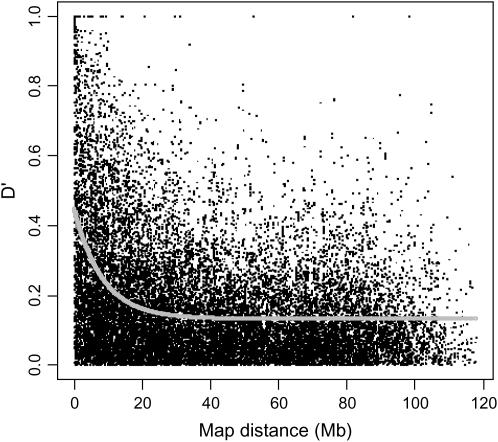
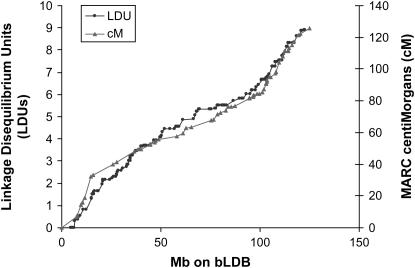
Lewontin's (1964) measure of LD, _D_′, was computed between all the pairs of 220 SNPs markers and is shown as a scatter plot of _D_′ against distance (Figure 3). Figure 3 indicates that while there is decay in LD with increasing distance, there is also extensive variability in the magnitude of _D_′ at any one distance. This, in large part, reflects wide local variations in the extent of LD across the chromosome, which is represented in an LD map. The average decline of LD with distance when the data are fitted to the Malecot model is also indicated in Figure 3. The constructed LD map of BTA6 using data for all 220 SNPs genotyped on 433 Australian dairy bulls has a total map length of 8.9 LDUs. Plotting LDU against kilobase locations from bLDB reveals a pattern of steps and plateaus reflecting the variation in the strength of LD at different chromosome locations (Figure 4). The larger steps have been shown in humans to correspond to the location of narrow regions of intense recombination (Zhang et al. 2002), corresponding to recombination hot spots. Small steps presumably reflect ancient recombination events. The mean swept radius for the whole map is 13.3 Mb, which is much larger than in humans (where it ranges from ∼0.02 to 0.05 Mb; De La Vega et al. 2005) and reflects much more extensive LD in cattle.
Figure 3.—
Distribution of _D_′-values observed between SNP pairs over physical distance (megabases) for BTA6. The shaded line corresponds to the fitted Malecot model that shows the average rate of decline of LD over the chromosome.
Figure 4.—
The LDU map and the MARC linkage map plotted against megabase location on the bLDB integrated map of BTA6.
Structure of LD along BTA6:
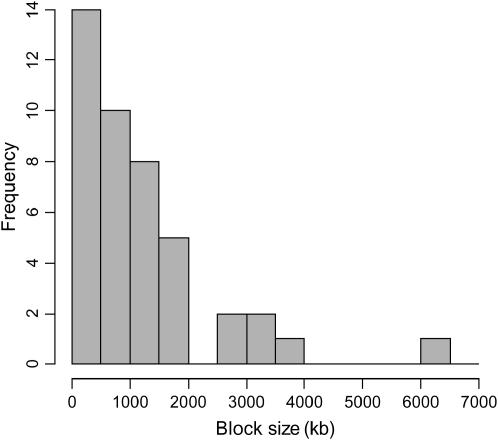
A total of 40 blocks with tracts of consecutive intervals spanning zero LDUs are observed along BTA6 (Figures 1 and 5). These collectively cover 41% of the chromosome with a mean block size of 1257 kb (range from 0.10 to 6144.3 kb, Table 1). There are four small blocks of <100 kb and 19 blocks >1 Mb long (Figure 1). A few of the smaller blocks are not visible in Figure 1 due to the scale. Alternative definitions of blocks (comprising consecutive intervals spanning 0.1, 0.2, 0.5, and 1.0 LDUs) are presented in Table 1, which indicates that up to 81% of BTA6 can be defined in the form of blocks such that strong LD (0.2 LDU) is observed between markers within blocks. There are 13 steps >0.2 LDUs long with the maximum being 0.48 LDU (Figure 1). The mean length derived from the integrated map for these intervals is 1427 kb.
Figure 5.—
Frequency distribution of the block size (with zero LDU within block) for BTA6.
TABLE 1.
Block definition and size distribution
| Minimum step(LDU) | No. of blocks | Minimum size (kb) | Maximum size (kb) | Mean (kb) | Total length of blocks (kb) | % coverage of chromosome |
|---|---|---|---|---|---|---|
| 0 | 40 | 0.10 | 6,144.26 | 1,256.78 | 50,271.11 | 41.02 |
| 0.1 | 46 | 0.03 | 8,236.14 | 1,651.75 | 75,980.35 | 62.00 |
| 0.2 | 42 | 36.37 | 9,194.78 | 2,369.87 | 99,534.48 | 81.23 |
| 0.5 | 22 | 1,894.40 | 15,793.61 | 5,367.26 | 118,079.75 | 96.36 |
| 1.0 | 11 | 2,718.06 | 29,170.23 | 10,734.52 | 118,079.75 | 96.36 |
| Step | 13 | 87.06 | 2,872.91 | 1,426.56 | 18,545.27 | 15.13 |
The relationship between LD and recombination rate:
The LD map shows a close relationship to the linkage map. This is despite the much lower resolution of the linkage map and the evolutionary variation captured in the LD map (Figure 4). Broad recombination hot regions situated, for example, at the beginning and end of the linkage map of BTA6 can now be seen to correspond to the regions where LD steps are clustered and blocks are small and numerous. Recombination cold spots correspond to regions dominated by longer tracks of extensive LD in the middle part of the chromosome.
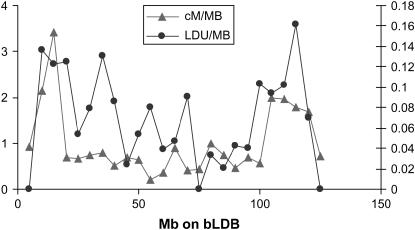
To understand the observed patterns of high and low LD over both small and large chromosome segments, it is necessary to understand the historical recombination rate. The extent to which LD is influenced by recombination was examined in the 56 intervals defined by the common markers on the bLDB bovine integrated map and MARC genetic map (http://www.marc.usda.gov/). Despite the variable length of the intervals on the genetic maps, a Pearson's product–moment correlation of 0.35 (P = 0.02) was observed between the centimorgans per megabase and the LDUs per megabase, after removing the zero and infinite values. The recombination rates and LD were also compared at regular intervals of 2, 5 (Figure 6), and 10 Mb. The correlations between centimorgans per megabase and LDUs per megabase for these intervals were 0.20 (P = 0.1), 0.49 (P = 0.02), and 0.69 (P = 0.02), respectively. It appears from the relationship between centimorgans per megabase and LDUs per megabase that variation in the recombination rate (hot and cold spots) along the chromosome is partly responsible for the block and step structure of LD seen in the LD map. In addition to the localized effects of recombination, other factors including selection are likely to be acting to maintain the LD block structure in the population.
Figure 6.—
Comparison of recombination rate (centimorgans per megabase) estimated from the MARC genetic map and LDUs per megabase estimated from the LDU map in regular intervals of 5 Mb on BTA6.
DISCUSSION
To our knowledge this is the first construction of a metric LD map for a chromosome other than human, based on phase-unknown genotypes of dense SNP markers. This map describes the LD structure over the whole chromosome and identifies regions of high and low LD. The map can be used for optimal marker placing for association mapping. It also identifies the large steps that may correspond to recombination hot spots.
The length of LD map reported here, namely of 8.9 LDUs, is much smaller when compared to an average human chromosome (which ranges from ∼1000 to 4300 LDUs; De La Vega et al. 2005), which presumably reflects the much smaller effective population size of cattle. Australian Holstein–Friesian cattle are under intense selection for milk production traits and have a small effective population size of ∼95 (Man 2004). Chromosome 6 is known to carry important quantitative trait loci for a number of production traits (Khatkar et al. 2004) and hence this chromosome may be under intense selection. Also, there has been a continuous importation of germplasm from different countries into Australia in addition to an ongoing within-country progeny-testing program (http://www.adhis.com.au/) and these may also contribute to the maintenance of LD.
The mean swept radius along the whole chromosome is 13.3 Mb, which is much larger than corresponding values in humans (ranging from ∼0.02 to 0.05 Mb) and indicates extensive LD in cattle. This estimate is smaller than the swept radius estimated in our previous study (18 Mb) based on low-density microsatellite data on the same chromosome (Khatkar et al. 2006), and this difference may reflect the more recent origin of microsatellite polymorphisms. LD based on SNPs has also been reported as shorter range when compared to LD based on microsatellite data in humans (Pritchard and Przeworski 2001).
There is some correspondence between low LD and high recombination frequency in the genetic map, suggesting that historical and contemporary recombination rates in particular genomic regions are related. A similar observation was made by Dawson et al. (2002) in the comparison of human genetic and LD maps of chromosome 22 and more recently for the whole genome (Tapper et al. 2005).
These initial map length estimates must be regarded as a first approximation for many reasons, especially since the accuracy of map positions of the SNP markers can affect map length and parameters used in calculation of the LD map. However, the use of the bLDB provides the best-known positions for SNP markers and a similar map integration approach was found to be accurate in deriving marker position in the human LDB before access to the full genome sequence (Tapper et al. 2001).
From the LD map derived from BTA6, it is possible to estimate the total number of LDUs in the bovine genome by extrapolation using the genetic map length of chromosome 6 and relating this to the total genome length. Assuming a length of 125 cM for chromosome 6 and a total length of 3000 cM in the bovine genome implies that the genome has ∼214 LDUs. It is likely that a number of SNPs spanning a range of frequencies will be required to screen each LD unit to provide efficient coverage of the bovine genome for whole-genome association mapping and further routine MAS applications. The short LD map of BTA6 in this study suggests that this type of cattle population is ideal for whole-genome association mapping. The total number of SNPs required for an efficient genomewide scan is anticipated to be much smaller than that required for such studies in humans. However, the very extensive LD will limit the level of resolution that can be achieved in fine mapping. At this point further analysis, particularly with respect to selection of informative SNPs, accommodation of a range of SNP allele frequencies, pattern of LD on other chromosomes, and the relationship to power for mapping, is required to develop an efficient panel for genomewide scans.
Acknowledgments
We thank Genetics Australia for semen samples, the Australian Dairy Herd Improvement Scheme for pedigree data, and Yasmin Husaini and other support staff in the laboratory for technical support. This research is supported by the Cooperative Research Centre for Innovative Dairy Products, Victoria, Australia.
References
- Altshuler, D., L. D. Brooks, A. Chakravarti, F. S. Collins, M. J. Daly et al., 2005. A haplotype map of the human genome. Nature 437**:** 1299–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson, E., G. R. Abecasis, S. Bumpstead, Y. Chen, S. Hunt et al., 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418**:** 544–548. [DOI] [PubMed] [Google Scholar]
- De La Vega, F. M., H. Isaac, A. Collins, C. R. Scafe, B. V. Halldorsson et al., 2005. The linkage disequilibrium maps of three human chromosomes across four populations reflect their demographic history and a common underlying recombination pattern. Genome Res. 15**:** 454–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan, J. B., A. Oliphant, R. Shen, B. G. Kermani, F. Garcia et al., 2003. Highly parallel SNP genotyping. Cold Spring Harbor Symp. Quant. Biol. 68**:** 69–78. [DOI] [PubMed] [Google Scholar]
- Farnir, F., W. Coppieters, J. J. Arranz, P. Berzi, N. Cambisano et al., 2000. Extensive genome-wide linkage disequilibrium in cattle. Genome Res. 10**:** 220–227. [DOI] [PubMed] [Google Scholar]
- Guo, S. W., and E. A. Thompson, 1992. Performing the exact test of Hardy-Weinberg proportion for multiple alleles. Biometrics 48**:** 361–372. [PubMed] [Google Scholar]
- Hawken, R. J., W. C. Barris, S. M. McWilliam and B. P. Dalrymple, 2004. An interactive bovine in silico SNP database (IBISS). Mamm. Genome 15**:** 819–827. [DOI] [PubMed] [Google Scholar]
- Heyen, D. W., J. E. Beever, Y. Da, R. E. Evert, C. Green et al., 1997. Exclusion probabilities of 22 bovine microsatellite markers in fluorescent multiplexes for semiautomated parentage testing. Anim. Genet. 28**:** 21–27. [DOI] [PubMed] [Google Scholar]
- Hinds, D. A., L. L. Stuve, G. B. Nilsen, E. Halperin, E. Eskin et al., 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307**:** 1072–1079. [DOI] [PubMed] [Google Scholar]
- Ke, X., W. Tapper and A. Collins, 2001. LDB2000: sequence-based integrated maps of the human genome. Bioinformatics 17**:** 581–586. [DOI] [PubMed] [Google Scholar]
- Ke, X., S. Hunt, W. Tapper, R. Lawrence, G. Stavrides et al., 2004. The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum. Mol. Genet. 13**:** 577–588. [DOI] [PubMed] [Google Scholar]
- Kent, W. J., 2002. BLAT—the BLAST-like alignment tool. Genome Res. 12**:** 656–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatkar, M. S., P. C. Thomson, I. Tammen and H. W. Raadsma, 2004. Quantitative trait loci mapping in dairy cattle: review and meta-analysis. Genet. Sel. Evol. 36**:** 163–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatkar, M. S., P. C. Thomson, I. Tammen, J. A. L. Cavanagh, F. W. Nicholas et al., 2006. Linkage disequilibrium on chromosome 6 in Australian Holstein-Friesian cattle. Genet. Sel. Evol. (in press). [DOI] [PMC free article] [PubMed]
- Lewontin, R. C., 1964. The interaction of selection and linkage. I. General considerations: heterotic models. Genetics 49**:** 49–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malecot, G., 1948. Les Mathématiques de l'Hérédité. Maison et Cie, Paris.
- Man, W. Y. N., 2004. Pedigree analysis of Holstein Friesians in Australia. Ph.D. Thesis, University of Sydney, Sydney, Australia.
- Maniatis, N., A. Collins, C. F. Xu, L. C. McCarthy, D. R. Hewett et al., 2002. The first linkage disequilibrium (LD) maps: delineation of hot and cold blocks by diplotype analysis. Proc. Natl. Acad. Sci. USA 99**:** 2228–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae, A. F., J. C. McEwan, K. G. Dodds, T. Wilson, A. M. Crawford et al., 2002. Linkage disequilibrium in domestic sheep. Genetics 160**:** 1113–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton, N. E., A. Collins, S. Lawrence and D. C. Shields, 1992. Algorithms for a location database. Ann. Hum. Genet. 56(3): 223–232. [DOI] [PubMed] [Google Scholar]
- Morton, N. E., W. Zhang, P. Taillon-Miller, S. Ennis, P. Y. Kwok et al., 2001. The optimal measure of allelic association. Proc. Natl. Acad. Sci. USA 98**:** 5217–5221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholas, F. W., 2005. Integrated and comparative maps in livestock genomics. Aust. J. Exp. Agric. 45**:** 1017–1020. [Google Scholar]
- Nsengimana, J., P. Baret, C. S. Haley and P. M. Visscher, 2004. Linkage disequilibrium in the domesticated pig. Genetics 166**:** 1395–1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odani, M., A. Narita, T. Watanabe, K. Yokouchi, Y. Sugimoto et al., 2006. Genome-wide linkage disequilibrium in two Japanese beef cattle breeds. Anim. Genet. 37**:** 139–144. [DOI] [PubMed] [Google Scholar]
- Pritchard, J. K., and M. Przeworski, 2001. Linkage disequilibrium in humans: models and data. Am. J. Hum. Genet. 69**:** 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snelling, W. M., E. Casas, R. T. Stone, J. W. Keele, G. P. Harhay et al., 2005. Linkage mapping bovine EST-based SNP. BMC Genomics 6**:** 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tapper, W. J., N. E. Morton, I. Dunham, X. Ke and A. Collins, 2001. A sequence-based integrated map of chromosome 22. Genome Res. 11**:** 1290–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tapper, W. J., N. Maniatis, N. E. Morton and A. Collins, 2003. A metric linkage disequilibrium map of a human chromosome. Ann. Hum. Genet. 67**:** 487–494. [DOI] [PubMed] [Google Scholar]
- Tapper, W., A. Collins, J. Gibson, N. Maniatis, S. Ennis et al., 2005. A map of the human genome in linkage disequilibrium units. Proc. Natl. Acad. Sci. USA 102**:** 11835–11839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tozaki, T., K. I. Hirota, T. Hasegawa, M. Tomita and M. Kurosawa, 2005. Prospects for whole genome linkage disequilibrium mapping in thoroughbreds. Gene 346**:** 127–132. [DOI] [PubMed] [Google Scholar]
- Zhang, W., A. Collins, N. Maniatis, W. Tapper and N. E. Morton, 2002. Properties of linkage disequilibrium (LD) maps. Proc. Natl. Acad. Sci. USA 99**:** 17004–17007. [DOI] [PMC free article] [PubMed] [Google Scholar]