A first-generation linkage disequilibrium map of human chromosome 22 (original) (raw)

Abstract

DNA sequence variants in specific genes or regions of the human genome are responsible for a variety of phenotypes such as disease risk or variable drug response1. These variants can be investigated directly, or through their non-random associations with neighbouring markers (called linkage disequilibrium (LD))2,3,4,5,6,7,8. Here we report measurement of LD along the complete sequence of human chromosome 22. Duplicate genotyping and analysis of 1,504 markers in Centre d'Etude du Polymorphisme Humain (CEPH) reference families at a median spacing of 15 kilobases (kb) reveals a highly variable pattern of LD along the chromosome, in which extensive regions of nearly complete LD up to 804 kb in length are interspersed with regions of little or no detectable LD. The LD patterns are replicated in a panel of unrelated UK Caucasians. There is a strong correlation between high LD and low recombination frequency in the extant genetic map, suggesting that historical and contemporary recombination rates are similar. This study demonstrates the feasibility of developing genome-wide maps of LD.

Similar content being viewed by others

Main

Present-day chromosomes are mosaics of ancestral chromosomes that have arisen through multiple recombination events in the past. Each copy of a chromosome within a population can be uniquely characterized on the basis of a specific pattern of sequence variants, which together comprise an individual ‘haplotype’. When these haplotypes do not occur in the population at the frequencies expected from the component variants, the variants are said to be associated or in linkage disequilibrium (LD). Characterizing the empirical patterns of LD across the genome will help to reconstruct the genetic history of human populations, enhance our understanding of the biological processes of recombination and natural selection, and facilitate association mapping studies that seek to localize genetic variants influencing complex traits and diseases. Previous studies of LD in humans have shown a high degree of variability, indicating that LD may extend between a few and several hundred kilobases1,2,3,4,5. For practical applications, however, the local patterns of haplotype conservation are of primary interest6,7,8, as the variability in LD overwhelms the average level. Therefore we characterized 59 independent haplotypes of human chromosome 22, derived from 77 members of three-generation pedigrees of the CEPH reference data set9. Using family samples helped to construct long haplotypes and detect genotyping error. All markers were selected from publicly available single-nucleotide polymorphisms (SNPs) and small insertions/deletions (indels)10,11,12 at regularly spaced intervals along the chromosome. A total of 951 of the 1,504 (63%) polymorphisms genotyped in the CEPH panels were common (minor allele frequency of ≥0.2; see Methods), which is similar to the proportion of common variants expected from comparing two chromosomes drawn from a constant size neutral population (60%). LD between pairs of markers was calculated using the measure D′, following its usage in previous empirical studies, and the _r_2 measure, which is preferred by population geneticists13.

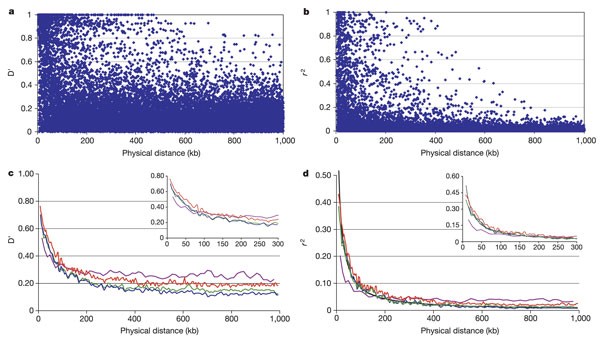
LD decays with increasing distance, but also shows extensive variability (Fig. 1a, b). Maximal D′ values extend up to distances over 400 kb, contrasting with occurrences of no detectable LD (D′ < 0.20) between markers less than 5 kb apart. The distribution of _r_2 values shows a similar degree of variability, differing from D′ mainly in measurement scale (Spearman rank correlation ρ(_r_2, D′) = 0.95). Similar results were obtained in analysis of two separate populations of unrelated individuals, also of Caucasian origin, one from the UK (90 individuals) and one from Estonia (51 individuals; Fig. 1c, d). In the combined CEPH and UK data sets, average D′ declines from 0.70 for adjacent markers to 0.11 for unlinked markers, whereas average _r_2 declines from 0.38 to 0.01. Although the two measures differ in scale, their decay profiles are similar.

Figure 1: Distribution of linkage disequilibrium on chromosome 22.*

a, b, Variability of D′ (a) and _r_2 (b) for the CEPH samples, using all pairwise values for markers with minor allele frequency > 0.20 separated by ≤1 Mb. c, d, Sliding window results of average D′ and _r_2 in successive bins of 200 markers (100 marker overlap). Insets provide enhanced views of the observed LD decay from 0–300 kb. CEPH, red; unrelated UK, green; combined CEPH/UK, dark blue; Estonia, violet

Full size image

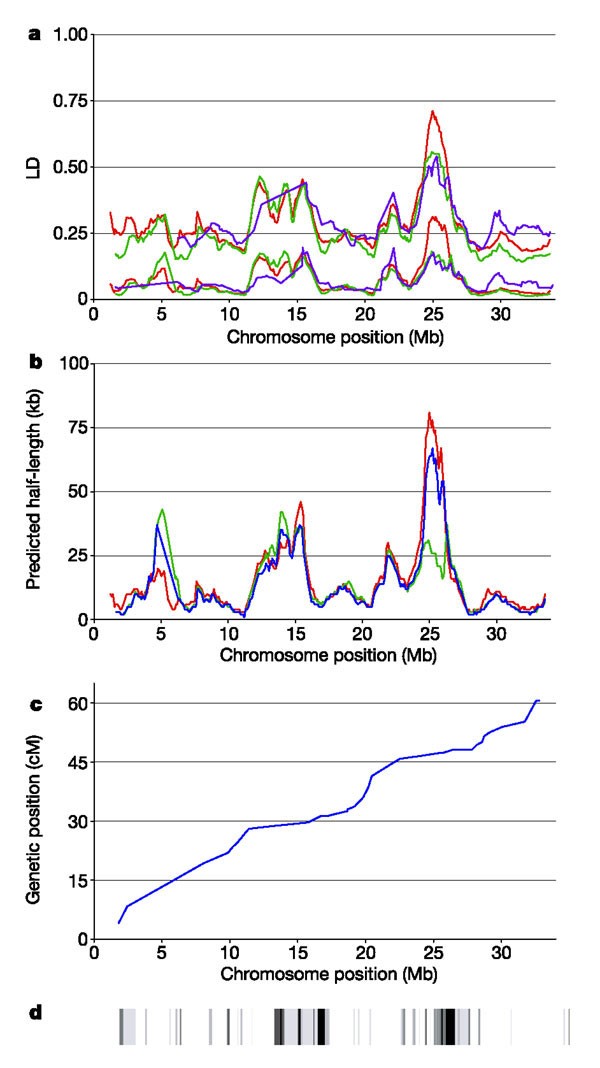
We assessed the pattern of LD along the chromosome by calculating average D′ and _r_2 for markers within contiguous 1.7-Mb stretches of DNA (sliding windows). In addition, statistical models of LD decay were fitted to summarize the patterns and to account for marker density. The results highlight areas with very high levels of LD, notably at positions 11–16 Mb and 21–27 Mb of the reference sequence (Fig. 2a, b). The degree to which these exceed background LD levels was confirmed by significance testing using extreme value distribution theory applied to ‘runs’ of LD (see Methods). Figure 2d shows various regions where LD is slightly above background levels (light bands), as well as shorter runs of extremely high disequilibrium relative to the rest of the chromosome (dark bands). These regional differences are not due to unequal marker spacing, as they align well with the model-fitting results (Fig. 2b) that account for such variability. The estimates were consistent between the CEPH and UK samples (Fig. 2b), indicating the usefulness of both family-based and unrelated samples for initial detection of long LD runs. The general patterns of LD also appear similar in the Estonian samples (Fig. 1a), but the marker density in the smaller Estonian data set (median 34.72 kb) is too coarse for formal delineation of specific regions. In the CEPH and UK samples, average D′ levels in the regions of high LD are 2–5 times greater than the background levels, presenting obvious distinctions of high and low LD tracts, whereas in the Estonian data, the highest LD region is less than twice the background level. Extrapolating these results to the genomic scale suggests that a median marker density greater than one marker per 35 kb is required for any first-generation map, and that, in the absence of family data, LD estimates in 100 chromosomes or fewer may be too variable for reproducible patterns at a broad scale.

Figure 2: Linkage disequilibrium across chromosome 22.

a, Average D′ and _r_2 coefficients (top and bottom groups, respectively) plotted in sliding windows containing all common polymorphisms separated by 50 and 500 kb in successive 1.7-Mb segments (1.6-Mb overlap). Sequence position 1 refers to the centromeric q-arm origin (ftp://ftp.sanger.ac.uk/pub/human/chr22/sequences/Chr_22/complete_sequence/Chr_22_19-05-2000.fa). The colour scheme is as in Fig. 1. b, Expected half length estimated from application of the model E(r_2) = 1/(1 + 4_Nc) to each sliding window. The model could not be fitted to the Estonian data because of the sparser marker density. c, Relationship between genetic and physical distance on chromosome 22 (refs 15, 16). d, Significant regions of excess LD (see Methods). The longest runs of LD (using f = 0.50_σ_D′) are shown in light grey; shorter runs of high LD are shown in dark grey (f = 1.00_σ_D′) and black (f = 1.50_σ_D′).

Full size image

There is considerable evidence that sites of recombination in humans are not randomly distributed, but are often localized into specific hotspots7,14. Current, low-resolution genetic maps can be used to model local recombination rates and provide additional predictors of LD beyond physical distance. Chromosome 22 has an elevated degree of recombination15,16,17, averaging 2.46 cM Mb-1 in our interpolated sex-averaged genetic map (see Supplementary Information), compared with the genome average of approximately 1.3 cM Mb-1. All components of the high LD tracts at 11–16 Mb and 21–27 Mb are situated in regions of exceptionally low recombination (<1 cM Mb-1; Fig. 2c) relative to the chromosome average. Indeed, nearly all of the high LD runs on chromosome 22 are located in regions of low recombination (Fig. 2d), a pattern previously noted in a localized region of this chromosome18, but which differs from a previous assessment of chromosome 22 microsatellite markers19. Collectively, the most exceptionally high-LD/low-recombination tracts cover about 9% of the chromosome, and 40% of the total variation in D′ along chromosome 22 can be explained by the (interpolated) genetic distance between markers. These results indicate that the extant genetic maps may be used in practice as guides to genomic regions having high or low LD, and are of immediate use in position-based association studies.

To search for other predictors of LD, we examined correlations between pairwise LD measures and various sequence features (Table 1). LD is positively correlated with gene density and short interspersed nuclear elements (SINEs) such as Alu repeats (which are features of (G + C)-rich sequence), and negatively correlated with long interspersed nuclear elements (LINEs), long terminal repeats (LTRs) and other DNA repeats ((G + C)-poor sequence). There is also a negative correlation between the (G + C)-rich sequence features and genetic distance. When genetic distance is factored out, by assessing sequence correlations with residual LD measures that are independent of genetic distance by multiple regression or using model-based regression residuals, nearly all of the relationships are reduced or effectively eliminated. The single exception to this collinearity occurs with LTRs, which maintain a significant negative correlation with LD independently of genetic distance (ρ = - 0.15). It is conceivable that LTRs predict recombination at a relatively fine resolution, whereas the currently available coarse genetic map predicts recombination at a broader resolution.

Table 1 Correlations between pairwise LD coefficients and sequence features

Full size table

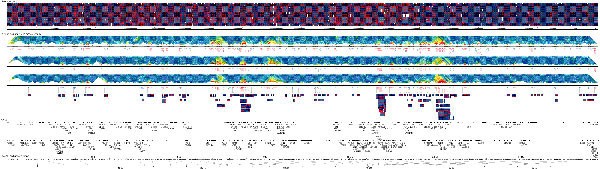
In addition to pairwise disequilibrium assessments, our data provide an opportunity to identify common conserved haplotypes along the chromosome. We conducted a systematic search for regions of limited haplotype diversity and strong disequilibrium in the combined CEPH and UK samples, in which we detected 97 ‘haplotype networks’ (see Methods), each including three or more markers (Fig. 3), including 329 out of 787 (41.8%) common polymorphisms and covering approximately 9.1 Mb of the long arm of chromosome 22 (22q). Interestingly, the two most common haplotypes are complementary at all sites in 55 of these networks. In some regions the networks overlap, reflecting the difficulty in precisely locating ancestral crossover events and possibly other phenomena such as gene conversion.

Figure 3: Haplotype networks on chromosome 22.

The figure is oriented with the leftmost position as the centromeric q-arm origin. The top panel shows the complete set of CEPH founder haplotypes (common alleles in blue; ambiguously phased or ungenotyped regions in white). Marker locations are given in the comb diagram underneath. The middle panels show 1-Mb-wide diagonal sections of colour-coded pairwise disequilibrium matrices30 for the CEPH families (top), UK unrelated (middle) and combined samples (bottom), respectively. Each sample is followed by a comb diagram for marker location and a pictorial representation of haplotype networks. Networks of three or four markers are in blue; longer networks are in red. The bottom panels show a detailed view of common haplotypes (>5%) for the combined data set. Within each block, haplotypes are listed in descending frequency. Gene composition and integrated genetic and physical maps are indicated. Transcribed sequences are grouped according to orientation15.

To view a large pdf of this image please click here: PDF (7.5 M)

Full size image

All of the common variants in any one of these networks can be surveyed with minimal genotyping effort. For example, in the CEPH families, the longest haplotype network extends 804 kb (at 11.83 Mb, including 16 markers) and a single network in the 21–27 Mb region includes 25 markers and extends 758 kb. These 25 markers could define up to 32 million chromosomes and in the absence of LD every chromosome in our sample would be unique. Instead, five haplotypes account for 76% of the CEPH founder chromosomes. Genotyping three SNP markers is sufficient to distinguish these five common haplotypes and retain 94.7% of haplotype heterozygosity. Similar long conserved haplotypes are present in the UK and combined samples.

Our ability to derive common haplotypes was significantly enhanced by the use of family-based samples (the CEPH panel). This is an important conclusion for a haplotype map project, because the relative usefulness of families will depend on empirical haplotype patterns20. Comparison of the haplotype frequency estimates from the unrelated UK compared with partially-phased CEPH chromosomes indicated that, for an average set of five consecutive markers, each CEPH founder contributed 1.91 times more information than an unrelated individual (Methods). This suggests that although genotyping extended pedigrees such as the CEPH families requires twice as much effort as that for unrelated individuals, the information for LD mapping is approximately equal. Given this similarity and the advantages of families for detection of genotyping errors, integration with meiotic maps and quality comparison across laboratories, the use of families for LD mapping is clearly preferable to unrelated individuals.

The primary motivation for construction of any LD map in the human genome is to facilitate identification and characterization of genetic variants for common complex diseases. The present data indicate that considerable information is available for fine mapping of disease loci even in first-generation maps such as our 15-kb chromosome-wide resolution. For example, linkages to schizophrenia and other psychiatric disorders have been reported around 22q12, near marker D22S278 (ref. 21) (at approximately 19.8 Mb); schizophrenia has also been associated with microdeletions in 22q11, near the velo-cardiofacial syndrome locus (∼5.6 Mb). Neither of these regions shows high LD in our data, suggesting that fine mapping may require a high density of markers. Conversely, linkage to type 2 diabetes has been reported around marker D22S423 (ref. 22) (approximately 23.8 Mb), which is on the edge of some of the longest tracts of high LD on the chromosome. Initial allelic association in this region may be facilitated by this extensive conservation.

Methods

Selection of markers, DNA samples and genotyping

Markers for genotyping were selected by walking along chromosome 22 in 15-kb steps through all available SNPs and small indels and choosing the nearest variant that was suitable for a unique polymerase chain reaction-based genotyping assay. Markers were genotyped in duplicate on 77 CEPH family DNAs and 90 unrelated UK Caucasian DNAs using the Third Wave Technologies Invader assay23, and on 51 unrelated Estonian DNAs using allele specific primer extension in microarray format24.

A final set of 1,504 markers were polymorphic in the CEPH DNA panel and were not rejected because of mendelian segregation errors, Hardy–Weinberg equilibrium deviations or other quality issues (the CEPH SNP set). There are 27 gaps of greater than 100 kb in this set (maximal gap of 293 kb), yielding a mean spacing of 22.95 kb and a median spacing of 15.07 kb. A total of 1,262 markers from the final CEPH set and 23 additional markers were successfully genotyped on the UK sample of unrelated individuals, for 1,286 markers on the UK Caucasians (the UK SNP set, median spacing of 17.53 kb, mean = 26.86 kb). We refer to the overlapping collection of CEPH and UK SNPs as the ‘combined’ marker set. The final Estonian SNP set had 908 SNPs, 661 of which had minor allele frequencies ≥0.20, and a median spacing of 34.72 kb (mean = 61.42 kb). The Estonian SNP set included 594 SNPs in common with the initial CEPH SNP set. The final data used in these analyses is available at http://www.sanger.ac.uk/HGP/Chr22.

Error checking

We tested all markers for Hardy–Weinberg equilibrium, ignoring family structure, and excluded from the analysis those where equilibrium was rejected at the 10-4 level. We verified familial relationships within the CEPH samples and checked that presumed unrelated UK individuals were truly unrelated using the GRR program25. In addition, we excluded all genotypes that produced mendelian errors or unlikely recombination patterns (P < 0.001) in the CEPH sample26. The duplicate genotyping resulted in a very low error rate, as indicated by mendelian segregation errors (480 out of 98,095 genotypes = 0.5%) and unlikely double recombinants (315 out of 98,095 genotypes = 0.3%) in the CEPH data set.

Haplotyping

For the CEPH pedigrees, we used MERLIN26 to list all alternate sets of non-recombinant founder haplotypes including small sets of neighbouring markers. Haplotype frequencies in families were then estimated using an expectation–maximization (E–M) algorithm27 (software available on request from G.R.A.). For unrelated individuals and the combined data set, we estimated haplotype frequencies using the E–M algorithm.

Pairwise disequilibrium and distance modelling

For pairwise comparisons we calculated D′ and r_2 following standard procedures13. We also fitted decay models to all pairwise coefficients within successive 1-Mb sliding windows: E(r_2_ij) = 1/(1 + 4_Nc ij), where N is the effective population size and c ij is the recombination fraction between markers i and j estimated from the physical distance between markers using the chromosome 22 average 1 Mb≈2 cM. We refer to the half-length of disequilibrium as the distance at which E(r_2_ij) = 0.5. Estimates from this model are largely independent of the underlying marker density.

Regions of excess disequilibrium

To define boundaries for regions of unusual disequilibrium, we used a method based on the Smith–Waterman algorithm28. For the i_th ordered marker pair within 500 kb of each other, we define the score S i = D′_i - k and then identify and compare high scoring segments using the Smith–Waterman accumulation approach and related statistical theory29. We used a penalty k = _D̄_′ × _fσ_D′ (with scale f = 0.5, 1.0, 1.5) to detect increasingly extreme runs of LD along the chromosome, where _σ_D′ refers to the standard deviation of all pairwise LD coefficients.

Haplotype networks

We defined regions of limited haplotype diversity as those in which five haplotypes accounted for 75% or more of all haplotypes observed in the population and in which disequilibrium between each marker and haplotypes of surrounding markers exceed 0.75. We searched for sets of markers (networks) that met these conditions using a single marker as a seed and adding as many neighbouring markers as possible. We used MERLIN26 to identify all non-recombinant haplotypes in a growing network and the E–M algorithm to estimate haplotype frequencies. We did not require markers in a network to be consecutive, but instead allowed up to six intervening markers to be excluded.

Comparison of families and unrelated individuals

Samples of unrelated individuals include more independent chromosomes, but less phase ambiguity exists in families. To compare the two approaches, we used the combined data set to estimate allele frequencies for each set of five consecutive markers. We then calculated the log-likelihood of each CEPH founder and unrelated individual using equilibrium allele frequencies and the haplotype frequencies estimated by E–M. The change in log-likelihood for each individual provides an indication of the amount of information contributed.

More detailed descriptions of marker selection, genotyping and error-checking protocols, genotyped marker characteristics and statistical procedures are provided as Supplementary Information.Footnote 1

Notes

1. *Figure 2d was published incorrectly in the AOP version of this paper on 10 July 2002. In the AOP publication, Fig. 2d was scaled incorrectly, so that it did not align with the panels above. This error was corrected on 1 August 2002.

References

1. Kruglyak, L. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nature Genet. 22, 139–144 (1999)
   Article CAS Google Scholar
2. Taillon-Miller, P. et al. Juxtaposed regions of extensive and minimal linkage disequilibrium in human Xq25 and Xq28. Nature Genet. 25, 324–328 (2000)
   Article CAS Google Scholar
3. Eaves, I. A. et al. The genetically isolated populations of Finland and Sardinia may not be a panacea for linkage disequilibrium mapping of common disease genes. Nature Genet. 25, 320–323 (2000)
   Article CAS Google Scholar
4. Abecasis, G. R. et al. Extent and distribution of linkage disequilibrium in three genomic regions. Am. J. Hum. Genet. 68, 191–197 (2001)
   Article CAS Google Scholar
5. Reich, D. E. et al. Linkage disequilibrium in the human genome. Nature 411, 199–204 (2001)
   Article ADS CAS Google Scholar
6. Daly, M. J., Rioux, J. D., Schaffner, S. F., Hudson, T. J. & Lander, E. S. High-resolution haplotype structure in the human genome. Nature Genet. 29, 229–232 (2001)
   Article CAS Google Scholar
7. Jeffreys, A. J., Kauppi, L. & Neumann, R. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nature Genet. 29, 217–222 (2001)
   Article CAS Google Scholar
8. Patil, N. et al. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294, 1719–1723 (2001)
   Article ADS CAS Google Scholar
9. Weissenbach, J. et al. A second-generation linkage map of the human genome. Nature 359, 794–801 (1992)
   Article ADS CAS Google Scholar
10. Dawson, E. et al. A SNP resource for human chromosome 22: extracting dense clusters of SNPs from the genomic sequence. Genome Res. 11, 170–178 (2001)
    Article CAS Google Scholar
11. Mullikin, J. C. et al. An SNP map of human chromosome 22. Nature 407, 516–520 (2000)
    Article ADS CAS Google Scholar
12. Sachidanandam, R. et al. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409, 928–933 (2001)
    Article ADS CAS Google Scholar
13. Weir, B. S. Genetic Data Analysis II (Sinauer Associates, Sunderland, Massachusetts, 1996)
    Google Scholar
14. Petes, T. D. Meiotic recombination hot spots and cold spots. Nature Rev. Genet. 2, 360–369 (2001)
    Article CAS Google Scholar
15. Dunham, I. et al. The DNA sequence of human chromosome 22. Nature 402, 489–495 (1999)
    Article ADS CAS Google Scholar
16. Yu, A. et al. Comparison of human genetic and sequence-based physical maps. Nature 409, 951–953 (2001)
    Article ADS CAS Google Scholar
17. Payseur, B. A. & Nachman, M. W. Microsatellite variation and recombination rate in the human genome. Genetics 156, 1285–1298 (2000)
    CAS PubMed PubMed Central Google Scholar
18. Eisenbarth, I., Striebel, A. M., Moschgath, E., Vogel, W. & Assum, G. Long-range sequence composition mirrors linkage disequilibrium pattern in a 1.13 Mb region of human chromosome 22. Hum. Mol. Genet. 10, 2833–2839 (2001)
    Article CAS Google Scholar
19. Huttley, G. A., Smith, M. W., Carrington, M. & O'Brien, S. J. A scan for linkage disequilibrium across the human genome. Genetics 152, 1711–1722 (1999)
    CAS PubMed PubMed Central Google Scholar
20. Thompson, E. A., Deeb, S., Walker, D. & Motulsky, A. G. The detection of linkage disequilibrium between closely linked markers: RFLPs at the AI-CIII apolipoprotein genes. Am. J. Hum. Genet. 42, 113–124 (1988)
    CAS PubMed PubMed Central Google Scholar
21. Pulver, A. E. et al. Sequential strategy to identify a susceptibility gene for schizophrenia: report of potential linkage on chromosome 22q12-q13.1: Part 1. Am. J. Med. Genet. 54, 36–43 (1994)
    Article CAS Google Scholar
22. Ghosh, S. et al. The Finland–United States investigation of non-insulin-dependent diabetes mellitus genetics (FUSION) study. I. An autosomal genome scan for genes that predispose to type 2 diabetes. Am. J. Hum. Genet. 67, 1174–1185 (2000)
    CAS PubMed PubMed Central Google Scholar
23. Mein, C. A. et al. Evaluation of single nucleotide polymorphism typing with invader on PCR amplicons and its automation. Genome Res. 10, 330–343 (2000)
    Article CAS Google Scholar
24. Kurg, A. et al. Arrayed primer extension: solid-phase four-colour DNA resequencing and mutation detection technology. Genet. Test 4, 1–7 (2000)
    Article CAS Google Scholar
25. Abecasis, G. R., Cherny, S. S., Cookson, W. O. & Cardon, L. R. GRR: graphical representation of relationship errors. Bioinformatics 17, 742–743 (2001)
    Article CAS Google Scholar
26. Abecasis, G. R., Cherny, S. S., Cookson, W. O. & Cardon, L. R. Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nature Genet. 30, 97–101 (2001)
    Article Google Scholar
27. Weir, B. S. & Cockerham, C. C. Estimation of linkage disequilibrium in randomly mating populations. Heredity 42, 105–111 (1979)
    Article Google Scholar
28. Smith, T. F. & Waterman, M. S. Identification of common molecular subsequences. J. Mol. Biol. 147, 195–197 (1981)
    Article CAS Google Scholar
29. Karlin, S. & Altschul, S. F. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl Acad. Sci. USA 87, 2264–2268 (1990)
    Article ADS CAS Google Scholar
30. Abecasis, G. R. & Cookson, W. O. GOLD—graphical overview of linkage disequilibrium. Bioinformatics 16, 182–183 (2000)
    Article CAS Google Scholar

Download references

Acknowledgements

The authors thank the Wellcome Trust for support, A. Edwards for preparation of CEPH family DNA, J. Collins for assistance with chromosome 22 annotation, and M. Holgate for the genotype data extraction programs. We also thank E. Beaty and N. Jarvis. L.R.C. thanks the Wellcome Trust and the NIH for support. A.M. was supported by the Estonian Ministry of Education and an EstSF grant.

Author information

Author notes

1. Elisabeth Dawson, Gonçalo R. Abecasis and Jaak Vilo: These authors contributed equally to this work

Authors and Affiliations

1. The Wellcome Trust Sanger Institute, Wellcome Trust Genome Campus, Hinxton, CB10 1SA, Cambridge, UK
   Elisabeth Dawson, Suzannah Bumpstead, Yuan Chen, Sarah Hunt, David M. Beare, Jagjit Pabial, Thomas Dibling, Emma Tinsley, Susan Kirby, David Carter, Marianna Papaspyridonos, Simon Livingstone, Kate Rice, Panos Deloukas, David R. Bentley & Ian Dunham
2. Wellcome Trust Centre for Human Genetics, University of Oxford, Roosevelt Drive, OX3 7BN, Oxford, UK
   Gonçalo R. Abecasis, Richard Mott & Lon R. Cardon
3. Department of Biostatistics, University of Michigan, Ann Arbor, Michigan, 48109-2029, USA
   Gonçalo R. Abecasis
4. Third Wave Technologies Inc., Madison, Wisconsin, 53719-1256, USA
   Rocky Ganske
5. IMCB of the University of Tartu, 23 Riia Street, 51010, Tartu, Estonia
   Elin Lõhmussaar, Maido Remm, Tarmo Puurand, Ants Kurg & Andres Metspalu
6. Estonian Biocentre, University of Tartu, 23 Riia Street, 51010, Tartu, Estonia
   Maido Remm & Andres Metspalu
7. Asper Ltd., 3 Oru Street, 51014, Tartu, Estonia
   Elin Lõhmussaar, Jana Zernant, Neeme Tõnisson, Reedik Mägi & Tarmo Puurand
8. European Bioinformatics Institute, Wellcome Trust Genome Campus, Hinxton, CB10 1SD, Cambridge, UK
   Jaak Vilo

Authors

1. Elisabeth Dawson
   You can also search for this author inPubMed Google Scholar
2. Gonçalo R. Abecasis
   You can also search for this author inPubMed Google Scholar
3. Suzannah Bumpstead
   You can also search for this author inPubMed Google Scholar
4. Yuan Chen
   You can also search for this author inPubMed Google Scholar
5. Sarah Hunt
   You can also search for this author inPubMed Google Scholar
6. David M. Beare
   You can also search for this author inPubMed Google Scholar
7. Jagjit Pabial
   You can also search for this author inPubMed Google Scholar
8. Thomas Dibling
   You can also search for this author inPubMed Google Scholar
9. Emma Tinsley
   You can also search for this author inPubMed Google Scholar
10. Susan Kirby
    You can also search for this author inPubMed Google Scholar
11. David Carter
    You can also search for this author inPubMed Google Scholar
12. Marianna Papaspyridonos
    You can also search for this author inPubMed Google Scholar
13. Simon Livingstone
    You can also search for this author inPubMed Google Scholar
14. Rocky Ganske
    You can also search for this author inPubMed Google Scholar
15. Elin Lõhmussaar
    You can also search for this author inPubMed Google Scholar
16. Jana Zernant
    You can also search for this author inPubMed Google Scholar
17. Neeme Tõnisson
    You can also search for this author inPubMed Google Scholar
18. Maido Remm
    You can also search for this author inPubMed Google Scholar
19. Reedik Mägi
    You can also search for this author inPubMed Google Scholar
20. Tarmo Puurand
    You can also search for this author inPubMed Google Scholar
21. Jaak Vilo
    You can also search for this author inPubMed Google Scholar
22. Ants Kurg
    You can also search for this author inPubMed Google Scholar
23. Kate Rice
    You can also search for this author inPubMed Google Scholar
24. Panos Deloukas
    You can also search for this author inPubMed Google Scholar
25. Richard Mott
    You can also search for this author inPubMed Google Scholar
26. Andres Metspalu
    You can also search for this author inPubMed Google Scholar
27. David R. Bentley
    You can also search for this author inPubMed Google Scholar
28. Lon R. Cardon
    You can also search for this author inPubMed Google Scholar
29. Ian Dunham
    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence toLon R. Cardon or Ian Dunham.

Ethics declarations

Competing interests

Some of the authors are supported by companies specializing in genotyping technologies,

which thus have financial interests in the outcomes of this paper. In particular, R.G. is supported

by Third Wave Technologies Inc., and E.L., J.Z., N.T., M.R., R.M., T.P. and A.M. are supported by Asper Ltd.

Supplementary information

Rights and permissions

About this article

Cite this article

Dawson, E., Abecasis, G., Bumpstead, S. et al. A first-generation linkage disequilibrium map of human chromosome 22.Nature 418, 544–548 (2002). https://doi.org/10.1038/nature00864

Download citation

• Received: 31 December 2001
• Accepted: 07 May 2002
• Published: 10 July 2002
• Issue Date: 01 August 2002
• DOI: https://doi.org/10.1038/nature00864