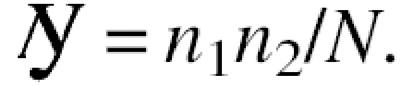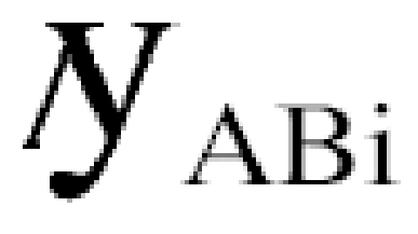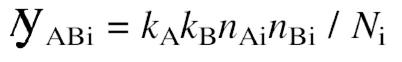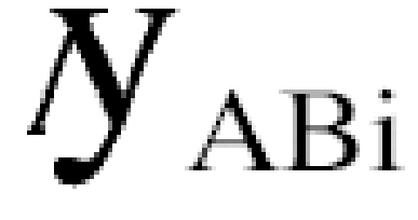On the number of protein–protein interactions in the yeast proteome (original) (raw)
Abstract
Using two different approaches, we estimated that on average there are about five interacting partners per protein in the proteome of the yeast Saccharomyces cerevisiae. In the first approach, we used a novel method to model sampling overlap by a Bernoulli process, compared the results of two independent yeast two-hybrid interaction screens and tested the robustness of the estimate. The most stable estimate of five interactors per protein was obtained when the three most highly connected nodes in the protein interaction network were removed from the analysis (eight interactors per protein if those nodes were kept). In the second approach, we analysed a published high-confidence subset of putative interaction data obtained from multiple sources, including large-scale two-hybrid screens, complex purifications, synthetic lethals, correlated gene expression, computational predictions and previous annotations. Strikingly, the estimate was again five interactors per protein. These estimates suggest a range of ∼16 000–26 000 different interaction pairs in the yeast, excluding homotypic interactions. We also discuss the approaches to estimating the rate of homotypic interactions.
INTRODUCTION
Scale-up of protein–protein interaction screens using the yeast two-hybrid system has made it possible to analyse complete proteomes and identify thousands of interactors. Surprisingly, recent proteome-wide screens in the yeast Saccharomyces cerevisiae (1,2) have yielded very little overlap in the detected interactions. This result was largely unexpected and has led to speculation on the high error rates in large-scale interaction screens and the need for an upward revision of the number of protein interactions in yeast (3).
A further indication of such revision is given by mass-spectrometry studies of purified protein complexes (4,5), which have also produced little overlap with each other, as well as with the interactions detected by the yeast two-hybrid approach (e.g., 7% for tandem affinity purification method). However, these methods do not provide information on pairwise interactions so the direct comparison with two-hybrid data is not straightforward.
Estimating the total number of interactions would allow one to understand the complexity of the protein interaction network, which is often represented as a graph with N nodes corresponding to individual proteins and E edges corresponding to interactions between them. The yeast interaction network contains some 6300 nodes but the number of edges is unknown. In graph theory, the term ‘degree’ is used to define the number of edges for a given node. Averaging across all nodes one can define a ‘mean degree’ of the network (2_E_/N), which would represent an average number of interactions per protein. So, in order to calculate the total number of interactions we need to estimate the mean degree of the interaction network.
Previous estimates of the numbers of interactions per protein in the yeast varied between 0.1 and 24 with estimates of the total number of protein interactions in Saccharomyces cerevisiae corresponding to a narrower range from 10 000 to 40 000 (3,6,7). In each of the two large-scale yeast screens (1,2), the number of interactions, E, was close to the number of proteins, N, involved. This gives an estimate of about two interactions per protein (2_E_/N) and <6500 interactions in the whole proteome.
Here, we attempt to estimate the number of interactions using two different approaches, both of them integrating information from more than one source. Strikingly, if the most robust probabilistic estimate is chosen and three nodes are removed, the estimates produced by both approaches actually coincide: the mean degree of the interaction network appears to be about five, thus the total number of different interacting protein pairs in the yeast proteome is ∼16 000. If the three nodes are kept, the mean degree is about eight and the total number of interacting protein pairs grows to 26 000.
MATERIALS AND METHODS
Estimating the number of interactions from sampling overlap
We estimated the number of interactions from the observed overlap between the interaction datasets, using the fact that sampling of interactions for a given protein by two independent experimental efforts can be viewed as a Bernoulli process yielding a binomial distribution. This approach can be easily illustrated on the example of picking in turn (and placing back) _n_1 and _n_2 objects from a box containing a total of N objects. The expected number of objects picked twice will then be
Since
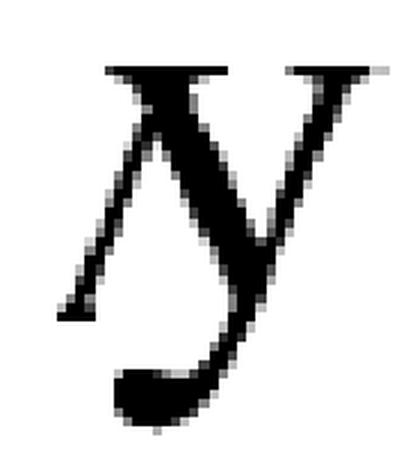
is the average measure of overlap between samples, every single pair of drawings can result in a wrong estimate but they will converge after a large number of trials.
Large-scale yeast two-hybrid screens represent such sampling processes for all the interaction sequence tags (ISTs) detected. Thus, if the screen A detects _n_Ai interactions for a protein i and the screen B finds _n_Bi, then the expected number
of common interactions can be calculated as
where _N_i is the total number of interactions involving protein i, and _k_A and _k_B are correcting coefficients for false positives and negatives in screens A and B, respectively. Replacing the expected number
by the observed number of common interactions _n_ABi we can try to estimate an average number, n, of interactions per protein from the distribution of the _N_i calculated across the whole set, P, of proteins (set size _s_P) detected in interaction experiments by both methods as:
n = (_k_A_k_B / _s_P) Σi∈P _n_Ai_n_Bi / _n_ABi
Dealing with cases of no overlap
Some of the proteins do not have any common interactions detected by both methods and cannot be directly used in the estimate as zero overlap (_n_ABi = 0) results in an infinitely large _N_i. Nevertheless, we could still attempt to find an upper bound of n using a simple scenario of ‘forcing overlap by one interaction’. Here, we assume that one of the methods failed to detect a single interaction already found by the second method and we add this interaction artificially. This would set _n_ABi = 1 and increment the smallest of the numbers _n_Ai and _n_Bi by one, assuming that in the worst case there would be just a single common interaction identified by both methods. Thus, instead of infinity, we can give _N_i an upper bound of _n_Ai_n_Bi/1 = _n_Ai_n_Bi.
Minimizing error
We cannot directly estimate _k_A or _k_B but we can choose the most reliable subsets of data to minimize the number of false negative and positive interactions (so that _k_A_k_B→1). In a previous study (8) different yeast protein–protein interaction datasets were compared on the basis of their agreement with gene expression profiles. A simple requirement of multiply confirmed interacting pairs was found to significantly increase the reliability of the interaction data. For example, the ‘core’ data from Ito et al. (2) with three or more ISTs as well as the data from Uetz et al. (1) agreed with expression profiles significantly better than the whole or non-core datasets of Ito et al. (2) and hence were used in our calculations below.
We did not consider datasets such as MIPS (9) collected from numerous publications on small-scale interaction screens since the choices of baits and preys in those are mainly hypothesis driven—hence they cannot be considered random and are not appropriate for our estimates based on random sampling.
Testing stability of the estimate
The robustness of this approach was evaluated by taking out in turn each of the common proteins and their interactions and performing the calculations for a subnetwork of remaining proteins (excluding those having connections only with the removed protein). From the distribution of the resulting estimates (_n_k after removal of a protein k) the mean estimate _n_r of interactions per protein and standard deviation (SD) were determined. Z-score was calculated as |_n_k–_n_r|/SD. Removal of the highly connected proteins produced the largest changes as evidenced by the Z-score and the range of the distribution.
Estimating the number of interactions by integrating multiple data sources
We analysed putative interaction data obtained from multiple sources using a previously published dataset of putative interactions (10). We constructed an interaction subnetwork comprising only the interactions with two or more different lines of evidence. The average number of interactors per protein was then determined as 2_E_/N.
RESULTS
Identifying overlapping samples from yeast two-hybrid screens
After removing redundancy, we created set U containing 884 interactions between 973 proteins, compiled from Uetz et al. (1) with later additions from Schwikowski et al. (11), and set I, which represented the ‘core data’ from Ito et al. (2) with 754 interactions between 786 proteins. Homotypic interactions were not included in sets U and I and were not taken into account in the calculations. The union of both datasets comprised 1442 proteins while in common between the networks U and I there were 317 proteins, identified either as bait or prey or both.
One example of such a common network node (YGR119C) is shown in Figure 1. In this example, _n_A = 5, _n_B = 4, _n_AB = 2, so the expected total number of partners of YGR119C is N = 5×4/2 = 10, though only seven have been detected.
Figure 1.
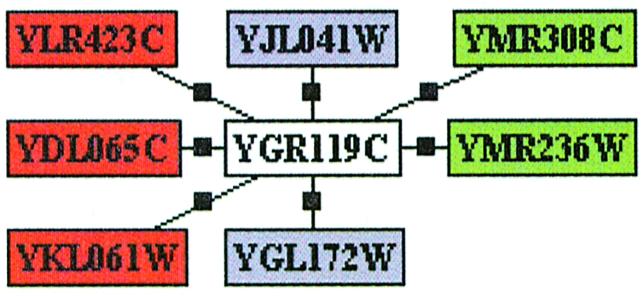
Overlap of the protein–protein interactions for YGR119C. Green and red rectangles correspond to interacting partners from set I and set U, respectively. Partners common between sets I and U are shown as blue rectangles. In this example, _n_A = 5, _n_B = 4, _n_AB = 2, so the expected total number of partners of YGR119C is N = 10, though only seven are currently detected.
However, 169 of the proteins common between sets U and I had no common interaction partner identified by both experimental groups and only 148 proteins had one or more interactions shared by the two datasets.
Removing three highly connected network nodes
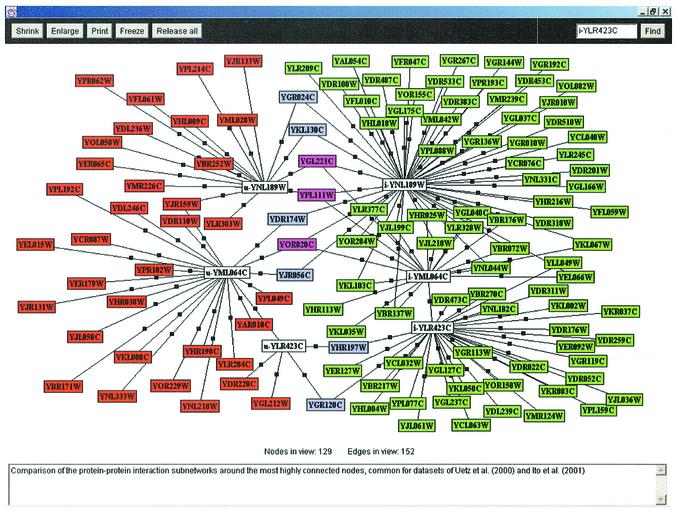
For three proteins, estimates of the interaction partners _N_i were very large (>100): 240 for YML064C (gene name TEM1, GTP-binding protein involved in termination of M-phase, ras superfamily), 233 for YNL189W (gene name SRP1, karyopherin alpha homolog) and 110 for YJR091C (gene name JSN1, benomyl-dependent tubulin mutant). These numbers are significantly higher than the estimates for the rest of the proteins, where the highest number is 64 interaction partners for YLR423C. Not surprisingly, among the nodes common between the two networks these are the most highly connected ones. Further, their common partners are too few in number, resulting in those elevated estimates. All of the interaction partners of these nodes are shown together in Figure 2 with the exception of the node YJR091C, which has zero overlap in both datasets.
Figure 2.
Overlap of the protein–protein interaction subnetworks. Subnetworks displayed are around the proteins encoded by YNL189W, YML064C and YLR423C (shown as white rectangles), the most highly connected nodes common for the datasets U and I (the u- and i- prefixes corresponds to sets U and I, respectively). The comparative display represents a screen shot of PINS (Protein Interaction Navigation System; Grigoriev, unpublished) software. Interaction partners are shown only for these three proteins. Color coding is as in Figure 1, while pink rectangles designate proteins linked to more than one of the above nodes.
As expected, YML064C, YNL189W and YJR091C also produced the largest changes in terms of robustness of the estimate (see below). Hence they have been removed from the network and their interactions omitted from the subsequent calculations. After the removal, the highest estimate of interaction partners was 55 for YLR423C.
Robustness of the estimate
We evaluated how robust our estimate was by taking out in turn each of the 317 common proteins (and corresponding interactions) and performing the calculations for a subnetwork of 316 remaining proteins (without adding artificial interactions). From the distribution of the resulting estimates the mean number of interactions per protein, n, and SD were determined (Table 1). Removal of the highly connected proteins above produced the largest changes: e.g., Z-score > 9.5 for YML064C, while the range (or the distance between the minimum and maximum) of the distribution was ∼17 SD. After elimination of the three nodes the same procedure was repeated and the estimate of n was much more robust: both the SD decreased >3-fold and the range of the distribution shrunk appreciably to some 14 SD (Table 1). Thus, removal of the highly connected nodes reduces the average number of interactions from eight to about five per protein.
Table 1. Estimates of the mean number of interactions per protein.
| Proteins excluded from network? | No | Yesa |
|---|---|---|
| Mean | 8.26 | 4.97 |
| SD | 0.17 | 0.05 |
| Rangeb (in SD units) | 17.14 | 14.09 |
| Rangeb | 2.92 | 0.72 |
Since 169 of the proteins had no common interaction partner (identified by both experimental groups), we tested the effect of adding singular artificial interactions to these to obtain ‘overlap by one interaction’, as described in Materials and Methods, and repeated the estimate. As expected, this did not change the estimate dramatically. The mean degree increased to 5.36 ± 0.06, indicating that among these 169 proteins the mean number of interacting partners was slightly below six if artificial interactions were added.
Integrating multiple data sources to estimate the number of interactions
We derived another estimate of the average number of interactors per protein from the data compiled by von Mering et al. (10) containing some 80 000 putative interactions collected from a number of different sources including direct experimental data (genome-wide yeast two-hybrid screens, complex purifications, synthetic lethals) and computed/inferred results (correlated gene expression and computational predictions).
We constructed an interaction subnetwork comprising only the interactions with at least two different lines of evidence, this threshold also having been used by von Mering et al. (10) for assigning a ‘high confidence’ qualifier to an interaction pair. In this network, 2455 interactions with high confidence involve 988 yeast proteins, resulting in 4.97 interactions per protein. This is a striking coincidence with the estimate in Table 1. Thus, both approaches suggest that on average there are about five interactors per yeast protein.
All these 80 000 putative interaction pairs obtained by genome-wide methods have been qualified with regard to co-occurrence of both proteins in the same complex as annotated at the MIPS website (http://mips.gsf.de/proj/yeast/catalogues/complexes/index.html), and co-occurring pairs have thus been marked as ‘previously annotated’ by von Mering et al. (10). We analysed the rate of the protein pair co-occurrence in MIPS complexes and found that it is about eight times higher in the high confidence subset than in the whole set of putative interactions (23 versus 2.9%). Since the presence of two proteins in the same complex most likely indicates an interaction between them, this confirms the better quality of the data in the high confidence subset.
DISCUSSION
We estimated the average number of interacting partners per protein in the proteome of the yeast S.cerevisiae, using two different approaches. In the first approach, we compared the results of two independent yeast two-hybrid interaction screens (1,2). Our estimate was derived from the observed overlap between the interaction datasets, assuming that sampling of interactions for a given protein by two independent experimental efforts can be viewed as a Bernoulli process yielding a binomial distribution.
The robustness of this approach was evaluated by taking out in turn each of the common proteins (and corresponding interactions) and performing the calculations for a subnetwork of remaining proteins. The most robust estimate of about five interactors per protein was obtained when the three most highly connected nodes in the protein interaction network were removed from the analysis. When they were kept in the network, the mean degree was about eight.
It is interesting to compare this number with the estimate obtained using the second approach. In that approach, we used the dataset compiled by von Mering et al. (10) where some 80 000 putative interactions collected from large-scale two-hybrid screens, complex purifications, synthetic lethals, correlated gene expression and computational predictions are assigned confidence based on confirmation by multiple methods. We analysed their compilation with regard to the average number of interacting partners and found that 2455 interactions with high confidence involve 988 yeast proteins, again resulting in about five interactions per protein.
What biases may affect these estimates? The most obvious is experimental bias. For instance, there may be enough similarity in the systematic errors of the large-scale yeast two-hybrid screens to lead to a biased measure of overlap between the datasets. Such errors may manifest themselves as false negatives when certain biological requirements that enable interactions are lacking in the yeast two-hybrid system: e.g., protein stability, localization and steric constraints, a free N-terminal domain of one of the proteins, physiological conditions unlike those of the yeast nucleus, etc. On the other hand, false positives may arise from reporter activation dependent on only one or the other of the fusion proteins, although these errors should be weeded out after a screen is done. For library screens it is known that some proteins appear to interact with many other proteins, and that other false positives may be a result of selection for genetic changes in the yeast that lead to activation of the reporter genes, etc. For the yeast interaction screens (more so than for human screens in the yeast two-hybrid system) false positives may arise via interaction of each of the two proteins with an intermediate protein (or several proteins).
Since we cannot directly estimate such error rates, we chose to use the more reliable subsets of the interaction data as inferred from an earlier comparison with gene expression results (8). Furthermore, as discussed in Ito et al. (2), the experimental systems used in the two screens are actually different regarding unique plasmid constructs as well as the strategy and stringency of selection (plasmid copy number and numbers of reporters). Different yeast two-hybrid systems often show different sensitivity with respect to the same interaction. This varies from one interaction to another to the extent that may well be considered random and lends support to the validity of our model for the estimate based on binomial distribution.
Sampling bias may also introduce errors. For instance, the chance of detecting highly connected nodes (proteins) in a non-saturated screen is higher than those linked to only a few interacting partners. However, we model sampling of interactions (edges between nodes) and not proteins. In fact, in the absence of experimental bias some proteins are more likely to be identified, but all detectable pairwise interactions have the same chance of being identified. In this case the bias may result from different levels of gene expression reflected in genome coverage of a constructed library.
We also identified two proteins, which appeared to interact with many other proteins in the large-scale screens but have little overlap between the two datasets and whose estimated number of interaction partners exceeded 230 (Fig. 2). Another protein was found with four interactions in set I, 22 in set U and no common interactions (the estimate produced by adding one artificial interaction exceeded 110 interactants for this node). Removal of these proteins produced the largest changes in the robustness. We thus made estimates both excluding and including these proteins since, on one hand, their connectivity may result from experimental bias despite our efforts to select the most reliable datasets, while on the other hand, their role may indeed involve interactions with so many partners (e.g., YNL189W codes for karyopherin alpha homolog participating in the protein transport action of the nuclear pore).
Our estimates are based on datasets smaller than the yeast genome/proteome (about 300 ORFs common between the yeast two-hybrid screens and some 1000 proteins in the high confidence subnetwork created from multiple sources). However, these datasets have shown good agreement with results obtained by other methods: yeast genome-wide expression profiling studies (8) and protein complexes annotated at the MIPS website (http://mips.gsf.de/proj/yeast/catalogues/complexes).
With five partners per protein, there should be ∼16 000 different interaction pairs in the yeast proteome comprising 6300 different proteins (6300×5/2 = 15750), and ∼26 000 with eight partners. This further narrows down the range of previous estimates from 10 000 to 40 000 (3,6,7,10). By scaling a postulated power-law degree distribution of the yeast protein network, Bader and Hogue (12) produced another estimate that is in the middle of our estimated range: ∼20 000. Another estimate, close to that presented here, of 15 000–20 000 has been published by Legrain et al. (13), although this estimate involved more of an educated guess than specific calculations.
Our estimate does not include homotypic interactions. Newman et al. (14) argued that homotypic interactions, especially those involving homodimers, are likely to be underrepresented in yeast two-hybrid screens due to preferential interaction of baits within a dimeric DNA binding protein over preys coming from solution. However, many homotypic interactions have been detected by both two-hybrid methods and repressor fusions (15) and they constitute some 4–7% (8) of the known yeast interaction sets (1,2,9). Hence, the total number of interactions will be higher.
One way to estimate that increase is to analyse the distribution of domains known to be involved in self-interactions. For example, homotypic interactions are often mediated by coiled-coil regions in proteins, and specific screens for interacting domains of those proteins identified an overlap with a predicted coiled-coil domain in many cases (15). Here, a rough order-of-magnitude estimate can be obtained from the fact that some 550 yeast proteins are predicted to contain two-stranded or three-stranded coiled coils (14).
About five interactions per protein have also been found in various Caenorhabditis elegans interaction screens (16), and this may well be a general average parameter for many eukaryotic proteomes. On the other hand, as mentioned above, the ability of proteins to interact with each other is generally ascribed to the presence of specific domains mediating interactions. It is interesting in this respect that the average domain content of human proteins is higher than that in yeast (17), which may lead to a higher number of interactants per human protein.
Acknowledgments
ACKNOWLEDGEMENTS
I would like to thank Stephan Schlenker for reading the manuscript and useful discussions, and the referees for insightful comments that helped improve the manuscript. This work was in part supported by the BMBF grant FKZ 0312551.
REFERENCES
- 1.Uetz P., Giot,L., Cagney,G., Mansfield,T.A., Judson,R.S., Knight,J.R., Lockshon,D., Narayan,V., Srinivasan,M., Pochart,P. et al. (2000) A comprehensive analysis of protein–protein interactions in Saccharomyces cerevisiae. Nature, 403, 623–627. [DOI] [PubMed] [Google Scholar]
- 2.Ito T., Chiba,T., Ozawa,R., Yoshida,M., Hattori,M. and Sakaki,Y. (2001) A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl Acad. Sci. USA, 98, 4569–4574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hazbun T.R. and Fields,S. (2001) Networking proteins in yeast. Proc. Natl Acad. Sci. USA, 98, 4277–4278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ho Y., Gruhler,A., Heilbut,A., Bader,G.D., Moore,L., Adams,S.L., Millar,A., Taylor,P., Bennett,K., Boutilier,K. et al. (2002) Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature, 415, 180–183. [DOI] [PubMed] [Google Scholar]
- 5.Gavin A.-C., Bosche,M., Krause,R., Grandi,P., Marzioch,M., Bauer,A., Schultz,J., Rick,J.M., Michon,A.M., Cruciat,C.M. et al. (2002) Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature, 415, 141–147. [DOI] [PubMed] [Google Scholar]
- 6.Walhout A.J., Boulton,S.J. and Vidal,M. (2000) Yeast two-hybrid systems and protein interaction mapping projects for yeast and worm. Yeast, 17, 88–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tucker C.L., Gera,J.F. and Uetz,P. (2001) Towards an understanding of complex protein networks. Trends Cell. Biol., 11, 102–106. [DOI] [PubMed] [Google Scholar]
- 8.Grigoriev A. (2001) A relationship between gene expression and protein interactions on the proteome scale: analysis of the bacteriophage T7 and the yeast Saccharomyces cerevisiae. Nucleic Acids Res., 29, 3513–3519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fellenberg M., Albermann,K., Zollner,A., Mewes,H.M. and Hani,J. (2000) Integrative analysis of protein interaction data. Intell. Syst. Mol. Biol., 8, 152–161. [PubMed] [Google Scholar]
- 10.von Mering C., Krause,R., Snel,B., Cornell,M., Oliver,S.G., Fields,S. and Bork,P. (2002) Comparative assessment of large-scale data sets of protein–protein interactions. Nature, 417, 399–403. [DOI] [PubMed] [Google Scholar]
- 11.Schwikowski B., Uetz,P. and Fields,S. (2000) A network of protein–protein interactions in yeast. Nat. Biotechnol., 18, 1257–1261. [DOI] [PubMed] [Google Scholar]
- 12.Bader G.D. and Hogue,C.W. (2002) Analyzing yeast protein–protein interaction data obtained from different sources. Nat. Biotechnol., 20, 991–997. [DOI] [PubMed] [Google Scholar]
- 13.Legrain P., Wojcik,J. and Gauthier,J.M. (2001) Protein–protein interaction maps: a lead towards cellular functions. Trends Genet., 17, 346–352. [DOI] [PubMed] [Google Scholar]
- 14.Newman J.R., Wolf,E. and Kim,P.S. (2000) A computationally directed screen identifying interacting coiled coils from Saccharomyces cerevisiae. Proc. Natl Acad. Sci. USA, 97, 13203–13208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Marino-Ramirez L. and Hu,J.C. (2002) Isolation and mapping of self-assembling protein domains encoded by the Saccharomyces cerevisiae genome using lambda repressor fusions. Yeast, 19, 641–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Davy A., Bello,P., Thierry-Mieg,N., Vaglio,P., Hitti,J., Doucette-Stamm,L., Thierry-Mieg,D., Reboul,J., Boulton,S., Walhout,A.J., Coux,O. and Vidal,M. (2001) A protein–protein interaction map of the Caenorhabditis elegans 26S proteasome. EMBO Rep., 2, 821–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lander E.S., Linton,L.M., Birren,B., Nusbaum,C., Zody,M.C., Baldwin,J., Devon,K., Dewar,K., Doyle,M., FitzHugh,W. et al. (2001) Initial sequencing and analysis of the human genome. Nature, 409, 860–921. [DOI] [PubMed] [Google Scholar]